探究RLC并联电路的复导纳特性

1.RLC并联电路的电压电流关系

由电阻R、电感L和电容C组成的并联电路，简称为RLC并联电路，如图3-33所示。

图3-32 例3-12图

根据相量形式的基尔霍夫电压定律，有

式中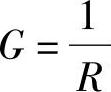，为电阻元件的电导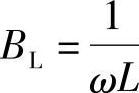；为电感元件的感纳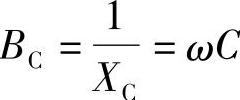；为电容元件的容纳；B=B_C-B_L为电纳。

图3-33 RLC并联电路

2.RLC并联电路的复导纳及相量图

与RLC串联电路的复阻抗对应，分析RLC并联电路用复导纳，这是正弦交流电路中另一个非常重要的概念。

式（3-52）中

Y=G+j（B_C-B_L） （3-53）

则有

可见，在RLC并联电路中，电流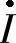相量与电压相量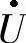之比为一复数Y，它的实部为电路的电导G，虚部为电路中的容纳B_C与感纳B_L之差B，称为电路的电纳，Y称为电路的复导纳，简称导纳，单位为西门子（S）。

将复导纳写成指数形式，则

式中

即

由以上分析可知，|Y|是复导纳Y的模，它等于此电路中电流的有效值与电压的有效值之比；φ′是复导纳的辐角，称为导纳角，它等于电流与电压的相位差角。它们只与电路参数及电源频率有关，而与电压及电流无关。同理，复导纳Y决定了电流、电压的有效值大小和相位间的关系。复导纳的模|Y|、电导G、电纳B构成一个直角三角形，如图3-34所示，称为导纳三角形。

图3-34 导纳三角形

3.RLC并联电路的性质

根据电路参数可得出RLC并联电路的性质，三种情况的相量图如图3-35所示。

1）当B_C>B_L时，φ′>0，即电流超前电压，电路呈容性；

2）当B_C<B_L时，φ′<0，即电流滞后电压，电路呈感性；

3）当B_C=B_L时，φ′=0，即电流与电压同相，电路呈阻性。

图3-35 RLC并联电路相量图

a）B_C>B_L b）B_C<B_L c）B_C=B_L

【例3-13】RLC并联电路，已知G=0.125S，B_L=0.318S，B_C=0.0445S，电流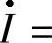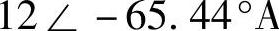，求复导纳和各支路电流。

解 1）复导纳Y=G+j（B_C-B_L）=0.125+j（0.0445-0.318）=0.125-j0.2735=0.3∠（-65.44°）S。

2）由相量形式的欧姆定律，得并联电路电压为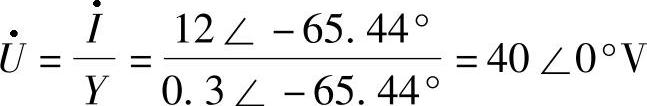，则各支路电流为

【例3-14】图3-36a所示为正弦交流电路的一部分，已知电流表I₁的读数为3A，I₂的读数为4A，求电流表A的读数。(www.xing528.com)

图3-36 例3-14图

a）电路图 b）相量图

解法一：以电压为参考相量，画出相量图如图3-36b所示，从相量图可以看出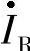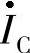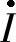，、、组成一直角三角形，故。

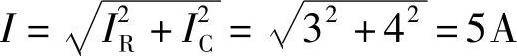解法二：设电压相量为，则，。

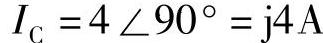由基尔霍夫电流定律，得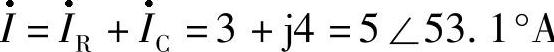，即电流表的读数为5A。

【思考与练习】

1）图3-37所示正弦交流电路，已知电源频率f=800Hz，C=0.046μF，R=2500Ω，求输出电压u₁与输入电压u₂之间的相位差，画出相量图。

2）已知某继电器的电阻为2kΩ，电感为43.3H，接在380V的工频交流电源上，求：

①线圈电流；

②电流与外加电压的相位差；

③相量图。

图 3-37

3）某RLC串联电路，电阻R=22Ω，电感L=0.6H，电容C=63.7μF，交流电源U=220V、f=50Hz。求：

①电路的感抗、容抗、电抗、阻抗、阻抗角；

②电路的电流；

③各元件的电压；

④相量图。

4）某RLC并联电路，已知R=50Ω，L=2mH，C=10μF，ω=5000rad/s，端口电流I=0.5A，求：

①电路的电导、感纳、容纳、电纳、导纳、导纳角；

②电路的端电压；

③各元件的电流；

④相量图。

5）图3-38图所示为正弦交流电路的一部分，已知电压表V₁的读数为6V，V₂的读数为8V，试求端口电压U。

6.在RLC串联电路中，总电压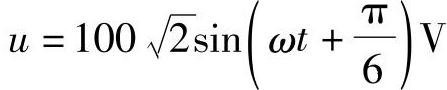，电流，ω=1000rad/s，L=1H，则R，C分别为（ ）。

A.10Ω，1μF B.10Ω，1000μF C.0.1Ω，1000μF

图 3-38