电感元件的作用及特点解析

1.电压和电流关系

实际线圈由电感和电阻构成，若把线圈中的电阻忽略不计，则线圈就仅含有电感。空载变压器、电力线路中限制短路电流的电抗器等都可视为纯电感负载，电感元件电路如图3-21a所示。

设电感中流过的正弦电流为

I_L=I_Lmsinωt （3-23）

则电感L两端的电压为

比较电压和电流关系式，可知：

1）电感元件两端的电压与电流同频率；

2）电感元件两端的电压超前电流90°；

3）电感元件两端的电压与电流的最大值与有效值之比为ωL；

令

X_L=ωL=2πfL （3-25）

把X_L称为感抗，它是用来表示电感元件对电流阻碍作用的一个物理量，与角频率成正比，单位是欧姆。f越高，X_L越大，意味着电感元件对电流的阻碍作用越大；f越低，X_L越小，即电感元件对电流的阻碍作用也越小。当f=0时X_L=0，表明电感元件对直流电流相当于短路。这就是电感元件本身所固有的“直流畅通，高频受阻”作用。

变换式（3-25），得

U_Lm=X_LI_Lm （3-26）

4）电感元件的电压、电流波形如图3-21b所示。

5）电感元件上电压与电流的相量关系为

电感元件的相量模型及相量图如图3-21c、d所示。

图3-21 电感元件

a）交流电路 b）波形图 c）相量模型 d）相量图(www.xing528.com)

2.电感元件的功率

（1）瞬时功率

电感元件的瞬时功率为

由式（3-28）可见，电感元件的瞬时功率p_L是一个幅值为UI，以两倍电源频率随时间按正弦规律变化的物理量，波形如图3-22所示。

（2）平均功率

由图3-22可见，正弦交流电路中的电感元件不断地与电源进行能量交换，但却不消耗能量。电感元件的平均功率为

P_L=0 （3-29）

（3）无功功率

纯电感L虽不消耗功率，但是它与电源之间有能量交换。工程中为了表示能量交换的规模大小，将电感瞬时功率的最大值定义为电感的无功功率，简称感性无功功率，用Q_L表示。即

图3-22 电感元件瞬时功率波形图

Q_L的基本单位是乏（var）。

无功功率并不是“无用”的功率，它表示电源与电感性负载之间能量的交换。

【例3-8】把一个电感量为0.35H的线圈接到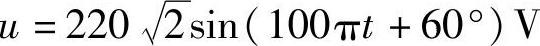的电源上，求线圈中电流瞬时值表达式。

解 由线圈两端电压的解析式可以得到U_L=220V，ω=100πrad/s，φ=60°。

电压u所对应的相量为。

线圈的感抗为X_L=ωL=100×3.14×0.35Ω≈110Ω。

因此可得。

因此通过线圈的电流瞬时值表达式为。