【摘要】：相量形式复数在复平面上还可以用相量表示，如图3-5所示。相量的长度r称为复数A的模，用|A|表示；相量与实轴的夹角，称为复数的辐角，用φ表示。复数的乘除运算复数的乘除运算一般用指数形式为AB=|A|∠φ1·|B|∠φ2=|AB|∠ 即复数的乘法运算就是将它们的模相乘，辐角相加；除法运算就是将它们的模除相除，辐角相减。图3-6 复数的加减运算
1.复数的表示
一个复数可以用以下几种形式来表示。
（1）直角坐标形式
A=a+jb （3-5）
a为复数的实部，b为复数的虚部。复平面上的点如图3-4所示。
（2）三角函数形式
A=A（cosφ+jsinφ） （3-6）
式中，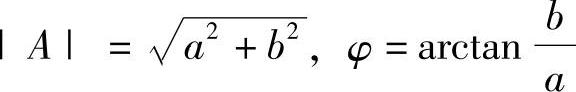
。复平面上的点如图3-4所示。
（3）相量形式
复数在复平面上还可以用相量表示，如图3-5所示。相量的长度r称为复数A的模，用|A|表示；相量与实轴的夹角，称为复数的辐角，用φ表示。
（4）指数形式
A=|A|ejφ （3-7）
复平面上的向量如图3-5所示。
图3-5 复平面上的向量
（5）极坐标形式(www.xing528.com)
A=|A|∠φ （3-8）
如图3-5所示。
2.复数的运算
有两个复数，A=a1+ja2=|A|∠φ1，B=b1+jb2=|B|∠φ2。
（1）复数的加减运算
复数的加减运算一般用代数形式表示为
A±B=（a1+ja2）±（b1+jb2）=（a1±b1）+j（a2±b2） （3-9）
即复数的加减运算就是把它们的实部和虚部分别相加减。
复数的加减也可以在复平面上用平行四边形法则求解，如图3-6所示。
（2）复数的乘除运算
复数的乘除运算一般用指数形式为
AB=|A|∠φ1·|B|∠φ2=|AB|∠（φ1+φ2） （3-10）
即复数的乘法运算就是将它们的模相乘，辐角相加；除法运算就是将它们的模除相除，辐角相减。
图3-6 复数的加减运算
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
