利用概率法求解尺寸链问题

从尺寸链各环分布的实际可能性出发进行尺寸链的计算，称为概率法（不完全互换法）。但是，由生产实践可知，在成批生产和大量生产中，零件实际尺寸的分布是随机的，多数情况下可考虑成正态分布或偏态分布。换句话说，如果加工或工艺调整中心接近公差带中心时，大多数零件的尺寸分布于公差带中心附近，靠近极限尺寸的零件数目极少。因此，可利用这一规律，将组成环公差放大，这样不但使零件易于加工，同时又能满足封闭环的技术要求，从而获得更大的经济效益。当然，此时封闭环超出技术要求的情况是存在的，但其概率很小，所以这种方法又称大数互换法。

10.3.1 基本公式

1.封闭环公差

由于在大批量生产中，封闭环A0的变化和组成环Ai的变化都可视为独立随机变量，且A0是Ai的函数，则可按随机函数的标准偏差的求法，得

式中 σ0，σ1，…，σm—— 封闭环和各组成环的标准偏差；

ξ1，ξ2，…，ξm—— 传递系数。

若组成环和封闭环尺寸偏差均服从正态分布，且分布范围与公差带宽度一致，且Ti =6σi ，此时封闭环的公差与组成环公差有如下关系：

如果考虑到各组成环的分布不为正态分布时，式中应引入相对分布系数 ki，对不同的分布，ki值的大小可由表10.3中查出，则

2.封闭环中间偏差

上偏差与下偏差之和的平均值为组成环的中间偏差，用Δ表示，即

当各组成环为对称分布时，封闭环中间偏差为

当组成环为其他不对称分布时，则平均偏差相对中间偏差之间偏移量为e称为相对不对称系数（对称分布e=0，见表10.3），这时式（10.12）应改为

3.封闭环、组成环极限偏差

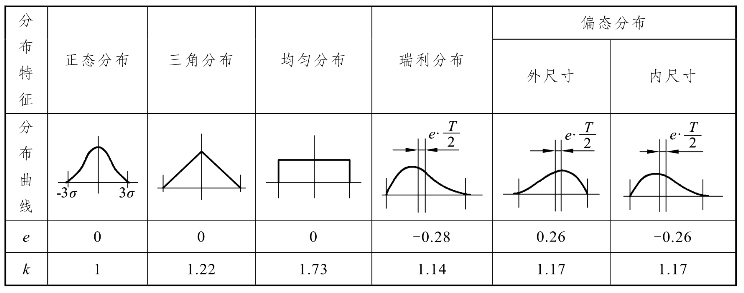
封闭环上偏差等于中间偏差加二分之一封闭环公差，下偏差等于中间偏差减二分之一封闭环公差，即

封闭环极限偏差

组成环极限偏差

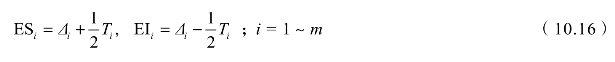
表10.3 相对不对称系数e和相对分布系数k

10.3.2 校核计算

【例10.3】用概率法解例10.1。

解：步骤（1）和（2）同例10.1。

（3）校核封闭环公差。

若组成环和封闭环尺寸偏差均服从正态分布，且分布范围与公差带宽度一致，且因该尺寸链为线性尺寸链，故K0=Ki=1，=1。T1=0.1 mm，T2=0.05 mm，T3=0.1 mm，T4=0.05 mm，T5=0.05 mm。

由于封闭环公差得计算值0.166 mm小于技术条件给定值0.35 mm，可见给定的组成环公差是正确的。

（4）确定封闭环中间偏差。

根据尺寸链图10.4（b）知，ξ1=-1，ξ2=-1，ξ3=1，ξ4=-1，ξ5=-1。按式（10.12）得 Δ1 =-0 .05mm ，Δ2 =-0 .025mm ，Δ3 =+0 .15mm ，Δ4 =-0 .025mm ，Δ5 =-0 .025mm 。则按式（10.13）计算得

Δ′0 = Δ3 - (Δ1 + Δ2 + Δ4 + Δ5)=+0.15+0.05+0.025+0.025+0.025=+0.275（mm）(www.xing528.com)

（5）校核封闭环极限偏差。

以上计算说明题干给出的组成环极限偏差是满足使用要求的。

10.3.3 设计计算

用概率法解尺寸链的设计计算和完全互换法解尺寸链方法和步骤基本相同，其目的仍是如何把封闭环的公差分配到各组成环上。用概率法解尺寸链的方法也分为“等公差法”和“等精度法”，只是公式发生了变化。采用“等公差法”时，各组成环的公差：

采用“等精度法”时，各组成环的公差等级系数：

【例10.4】用概率法中的“等精度法”解例10.2。

解：步骤（1）和（2）同例10.2。

（3）确定各组成环的公差。

① 若组成环和封闭环尺寸偏差均服从正态分布，且分布范围与公差带宽度一致，且因该尺寸链为线性尺寸链，故K0=Ki=1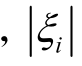=1。首先由表10.1查出各尺寸的公差因子：i1=2.52，i2=i5=0.73，i3=2.17，i4=1.56。然后按式（10.18）计算各组成环的平均公差等级系数a：

查表10.2，可知a=197在IT12和IT13之间，但更接近IT12=160，故公差等级取IT12级。则查公差等级表得：T1=400 μm，T2=T5=120 μm，T3=350 μm，T4=250 μm。

② 将上述数据代入下式，校核封闭环公差。

由于封闭环公差得计算值0.611 mm小于技术条件给定值0.75 mm，可见确定的组成环公差是正确的。

（4）确定各组成环的极限偏差。

① 确定A4为调整环，其余组成环根据“入体原则”配置，A1，A2，A5为外尺寸，按h配置；A3为内尺寸，按H配置。因此各组成环的极限偏差如下：

② 确定A4的极限偏差。

根据步骤（1）得 则各环的中间偏差为 Δ0 =+0 .375mm ， Δ1 =-0 .2mm ，Δ2 =-0 .06mm ， Δ3 =+0 .175mm ， Δ5 =-0 .06mm 。

根据尺寸链图10.5（b）可知，ξ1=-1，ξ2=-1，ξ3=1，ξ4=1，ξ5=-1。则按式（10.13）计算得

Δ0 = Δ3 + Δ4 -（ Δ1 + Δ2 +Δ5）=+0.175+ Δ4+0.2+0.06+0.06=+0.375（mm）

则 Δ4=-0.12（mm）

再按式（10.16）计算得

（5）校核封闭环极限偏差。

① 计算封闭环的中间偏差。

=Δ3 +Δ4 -Δ1 +Δ2 +Δ5 =+0 .375（mm）

② 校核封闭环的极限偏差。

以上计算说明给定的组成环极限偏差是满足使用要求的。

最后结果为

由例10.4和例10.2相比较可以看出，用概率法计算所确定的组成环公差值要比用完全互换法计算确定的组成环公差值要大，公差等级要更低，且在实际生产中出现不合格件的可能性又很小，因而能给生产带来显著的经济效益。