完全互换计算尺寸链又称极限法,它是从尺寸链中各环的极限尺寸出发进行尺寸链计算,按照这种方法计算的尺寸来加工工件各组成环,则无须进行挑选或修配就能将工件装到机器上,且能达到封闭环的精度要求。
10.2.1 基本公式
假设尺寸链的组成环数为m。A0为封闭环的基本尺寸,Ai为第i个组成环的基本尺寸,令A1~An为增环的基本尺寸,An+1~Am为减环的基本尺寸,则对于尺寸链的基本公式如下:
(1)封闭环的基本尺寸A0等于所有增环的基本尺寸之和减去所有减环的基本尺寸之和。

(2)封闭环的上极限尺寸A0max等于所有增环的上极限尺寸之和减去所有减环的下极限尺寸之和。

(3)封闭环的下极限尺寸A0min等于所有增环的下极限尺寸之和减去所有减环的上极限尺寸之和。

(4)封闭环的上偏差ES0等于所有增环的上偏差之和减去所有减环的下偏差之和。

(5)封闭环的下偏差EI0等于所有增环的下偏差之和减去所有减环的上偏差之和。

(6)封闭环公差T0等于所有组成环公差之和。

由式(10.6)看出:
(1)T0>Ti,即封闭环公差最大,精度最低。因此在零件尺寸链中应尽可能选取最不重要的尺寸作为封闭环。在装配尺寸链中,封闭环往往是装配后应达到的要求,不能随意选定。
(2)T0一定时,组成环数越多,则各组成环公差必然越小,经济性越差。因此,设计中应遵守“最短尺寸链”原则,即使组成环数尽可能少。
10.2.2 校核计算
校核计算的步骤如下:根据装配图确定封闭环,寻找组成环,画尺寸链图,判别增环和减环,由各组成环的基本尺寸和极限偏差验算封闭环的基本尺寸和极限偏差。最后校核几何精度设计的正确性。
【例10.1】在图10.4(a)所示齿轮部件中,设计要求齿轮右端面与挡环之间有间隙,现按工作条件,要求间隙A0=0.10~0.45 mm,已知:![]()
![]() 试问所规定的各零件的公差及极限偏差能否保证齿轮部件装配后的技术要求?
试问所规定的各零件的公差及极限偏差能否保证齿轮部件装配后的技术要求?
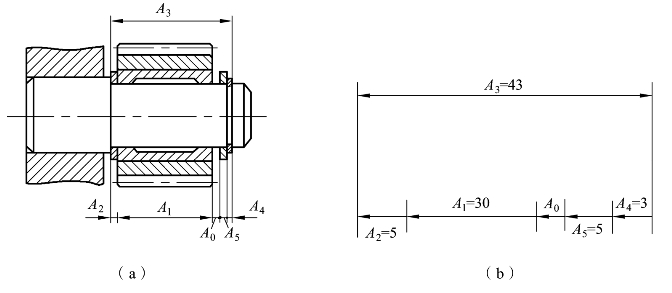
图10.4 齿轮部件尺寸链图
解:(1)画尺寸链图,判断增环、减环。
齿轮部件的间隙A0是装配过程最后形成的,是尺寸链的封闭环;A1~A5是5个组成环,如图10.4(b)所示,其中A3是增环,A1,A2,A4,A5是减环。
(2)按式(10.1)计算封闭环的基本尺寸。
A0=A3-(A1+A2+A4+A5)=43-(30+5+3+5)=0
即要求封闭环的尺寸为 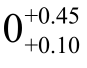 mm。
mm。
(3)按式(10.4)和式(10.5)校核封闭环的极限偏差。
ES0=ES3-(EI1+EI2+EI4+EI5)=+0.2-(-0.10-0.05-0.05-0.05)=+0.45(mm)
EI0=EI3-(ES1+ES2+ES4+ES5)=+0.10-(0+0+0+0)=+0.10(mm)
(4)按式(10.6)校核封闭环的公差
T0=T1+T2+T3+T4+T5=0.10+0.05+0.10+0.05+0.05=0.35(mm)
计算结果表明,所规定的零件公差及极限偏差恰好保证齿轮部件装配的技术要求。
10.2.3 设计计算
已知封闭环的基本尺寸和极限偏差,求各组成环的基本尺寸和极限偏差,即合理分配各组成环公差问题。各组成环公差的确定可用两种方法,即等公差法和等精度法。
1.等公差法
等公差法是假设各组成环的公差值是相等的,按照已知的封闭环公差T0和组成环环数m,计算各组成环的平均公差T,即

在此基础上,根据各组成环的尺寸大小、加工的难易程度对各组成环公差做适当调整,并满足组成环公差之和等于封闭环公差的关系。(https://www.xing528.com)
2.等精度法
等精度法是假设各组成环的公差等级是相等的。对于尺寸≤500 mm,公差等级在IT5~IT18,公差值的计算公式为T=ai,按照已知的封闭环公差T0和各组成环的公差因子ik,计算各组成环的公差等级系数a,即

为方便计算,各尺寸分段的i值列于表10.1。
表10.1 尺寸≤500 mm各尺寸分段的公差因子

求出a值后,将其与表10.2的数据相比较,得出最接近的公差等级后,可按该等级查标准公差表,求出组成环的公差值,从而进一步确定各组成环的极限偏差。各组成环的公差应满足组成环公差之和小于等于封闭环公差的关系。
表10.2 标准公差等级系数a

确定各组成环的极限偏差时,要先保留一个组成环作为调整环,其余组成环的极限偏差按“入体原则”确定,即内尺寸要素的下偏差为0,外尺寸要素的上偏差为0,非尺寸要素的公差带取对称分布。
计算完成后,还需进行校核,以保证计算的正确性。
【例10.2】图10.5(a)所示为某齿轮箱的一部分,根据使用要求,间隙A0=1~1.75 mm,若已知:A1=140 mm,A2=5 mm,A3=101 mm,A4=50 mm,A5=5 mm。试计算A1~A5各尺寸的极限偏差与公差。
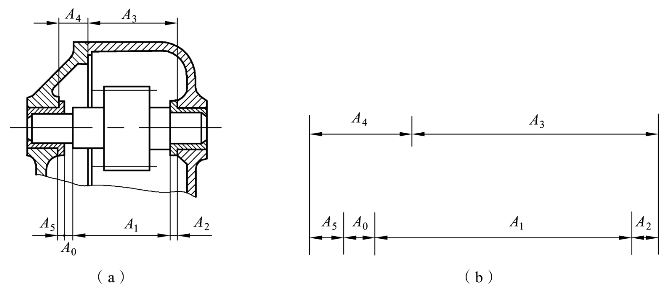
图10.5 齿轮箱部件尺寸链图
解:(1)画尺寸链图,区分增环、减环。
间隙A0是装配过程最后形成的,是尺寸链的封闭环。A1~A5是5个组成环,如图10.5(b)所示,其中A3,A4是增环,A1,A2,A5是减环。
(2)按式(10.1)计算封闭环的基本尺寸。
A0=A3+A4-(A1+A2+A5)=101+50-(140+5+5)=1(mm)
式中,A0为内尺寸,故下偏差取0,所以A0取![]() mm。
mm。
(3)用等精度法确定各组成环的公差。
首先由表10.1查出各尺寸的公差因子:i1=2.52,i2=i5=0.73,i3=2.17,i4=1.56。然后按式(10.8)计算各组成环的平均公差等级系数a:
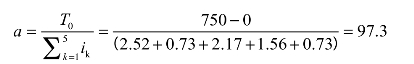
由表10.2查得,接近IT11级。确定A4为调整环,则根据各组成环的基本尺寸,从标准公差表查得各组成环的公差为T1=250 μm,T2=T5=75 μm,T3=220 μm。
T4=T0-(T1+T2+T3+T5)=750-(250+75+220+75)=130(μm)
再根据A4的基本尺寸查标准公差表,可取T4=100 μm(IT10)。
T1+T2+T3+T4+T5=250+75+220+100+75=720(μm)<750(μm)
所以按上述IT10和IT11级分配相应的组成环公差是合适的。
(4)确定各组成环的极限偏差。
① 确定A4为调整环,其余尺寸根据“入体原则”配置,A1,A2,A5为外尺寸,按h配置;A3为内尺寸,按H配置。因此除A4以外的各组成环的极限偏差如下:
![]()
② 计算A4的极限偏差。
EI0=EI3+EI4-(ES1+ES2+ES5)=0+EI4-(0+0+0)=0(mm),则EI4=0 mm。因为T4=100 μm,所以A4的极限偏差为 ![]() mm 。
mm 。
(5)校核封闭环极限偏差。
按式(10.4)和式(10.5)计算
EI0=EI3+EI4-(ES1+ES2+ES5)=0+0-(0+0+0)=0(mm)
ES0=ES3+ES4-(EI1+EI2+EI5)=+0.22+0.10-(-0.25-0.075-0.075)
=+0.72(mm)
故满足间隙A0在1~1.75 mm的要求。
最后结果为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




