泵设计中的欧拉方程：叶轮流量与扬程的关系

欧拉方程是泵设计时最重要的方程。可以采用不同的方式推导该方程。这里采用的方法为限制叶轮的控制体积以及描述进口和出口处的流体力和速度三角形的动量矩方程。

控制体积是用来建立平衡方程的一个假想的有限体积（叶槽）。可以为扭矩、能量及其他相关的流动参数建立平衡方程。动量矩方程是把质量流量和流速与叶轮直径相互关联起来的一个平衡方程。经常采用控制体积来描述叶轮，如图12.5中的1和2之间的控制体积。

我们所感兴趣的平衡是扭矩平衡。驱动轴传来的扭矩（T）相当于流体流过叶轮时产生的扭矩，此时质量流量为m=rQ，即

T=m⋅（r2⋅C2U-r1⋅C1U） （牛米） （12.12）

图12.5 叶轮的控制体积（叶槽）

把扭矩与角速度相乘就可以得到轴功率P2。同时，半径与角速度的乘积为切线速度，r2ω=U2。所以

根据能量方程，给液体增加的水功率可以写成叶轮内压力的增值ΔPtot与流量Q的乘积，

扬程的定义为

因此水功率的表达式可以写成(www.xing528.com)

如果假设流动没有损失，则水功率与机械功率相等，

该方程就是欧拉方程，表示的是叶轮的进口和出口的切线速度和绝对速度与扬程的关系。

如果对速度三角形采用余弦关系，泵的欧拉方程可以写成以下三个分量的总和：

离心力引起的静扬程

叶轮内流速变化引起的静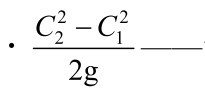扬程

动扬程

如果叶轮内没有水流流过并且假设进水没有漩涡分离，则根据公式（12.17）扬程仅取决于切线速度，式中C2U=U2：

设计泵时，通常假设进水没有漩涡分离，即C1U为零。