固体弹性过滤器：消除机械振动误差的利器

在驱动装置里使用齿轮装置时，容易由此而发生振动问题（参照图2.12.4a）。因此，必须用本原理将振动从发生点及时吸收、除去。除去振动干扰的方法是在机械和驱动装置之间接上能吸收振动的传动带（尤其是平带和V带，见图2.12.4b）。因为传动带是弹性体，所以高频率成分的振动难以向下方的机械传递。但是，即使有平带存在也必须注意还会有微小的振动发生。由于最近电动机的性能越来越好，如果可能的话可以用不会存在干扰的内装电动机，即在机械的内部装入电动机使其一体化，比用齿轮装置和传动带好。

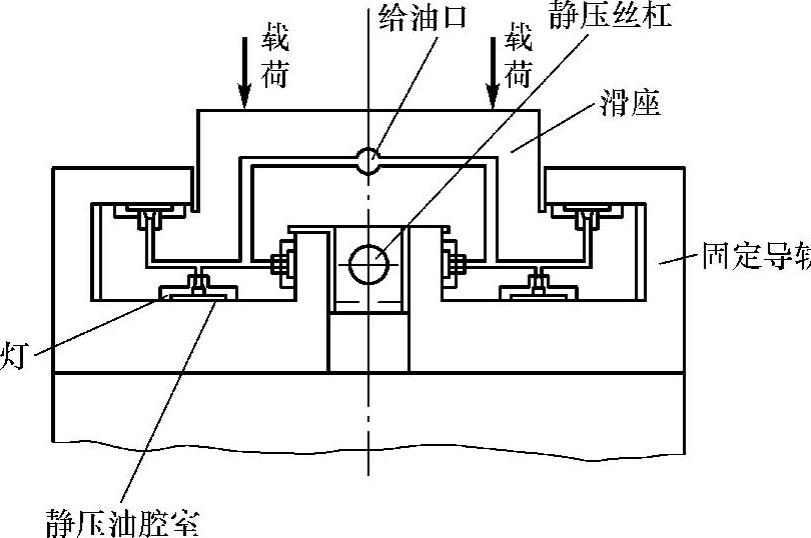
图2.12.2 油压静压导轨的工作台

注意：当传动带的刚性大而机械一侧的惯性矩过小，减振效果也不会好。而且，传动带本来精度也不高。例如用V带时，V带和带轮的啮合容易发生振动，因此相反地成了振源。

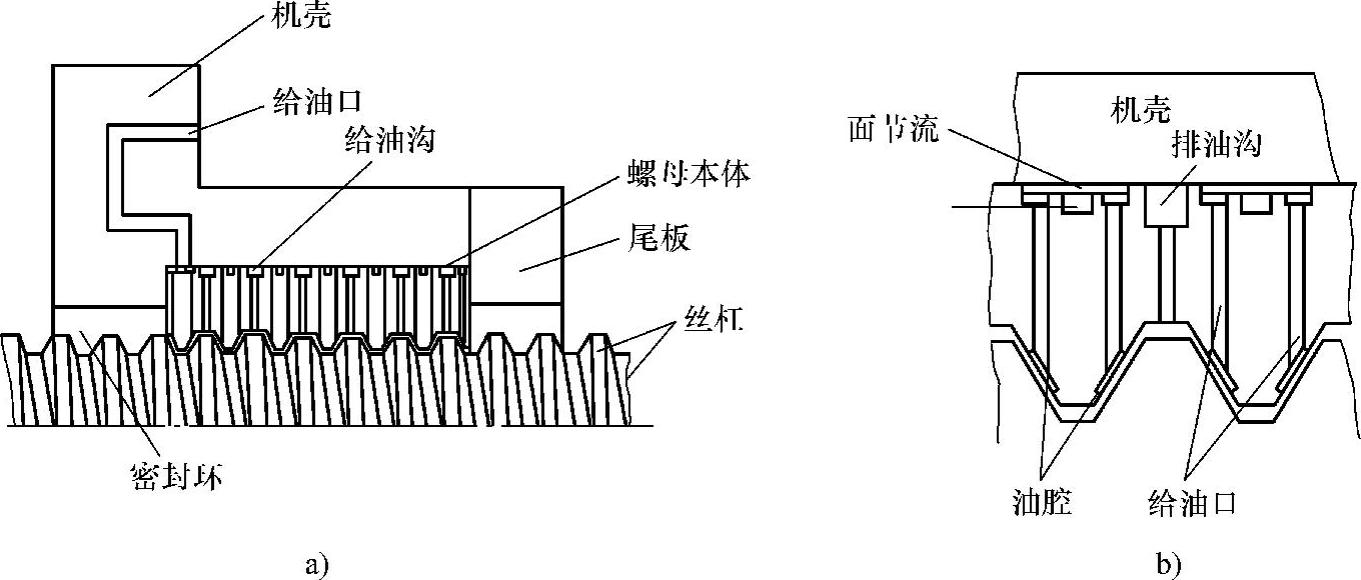
图2.12.3 油压静压丝杠

a）静压丝杠（全体图） b）静压丝杠（部分图）

下面是用丝杠驱动工作台的例子，用于高精度光栅尺数控划线机上，其构造如图2.12.5所示。干扰所发生的地方即工作台和螺母之间插有作为固体弹性过滤器的平板弹簧，用于吸收丝杠和工作台导轨之间的平行度误差。

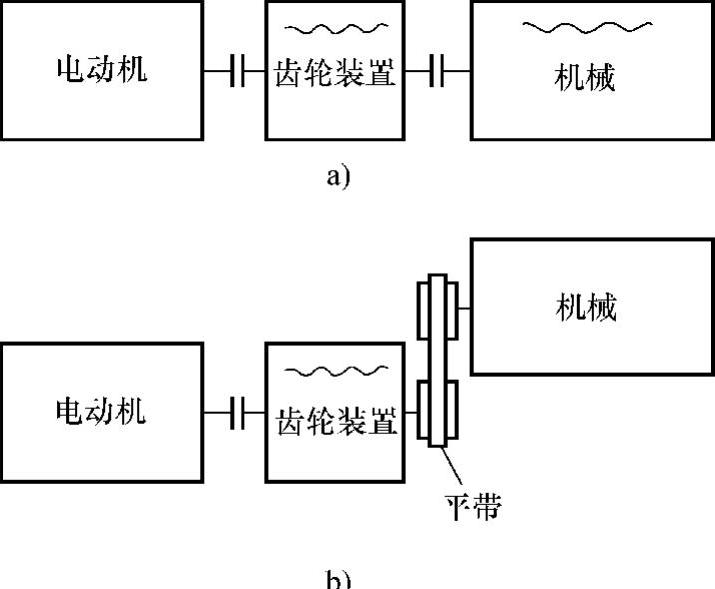
图2.12.4 用低刚性的元件吸收和消除干扰的实例

a）电动机、齿轮装置的干扰传递到机械里 b）把刚性低的元件（平带）插入动力传动链中以吸收和消除干扰

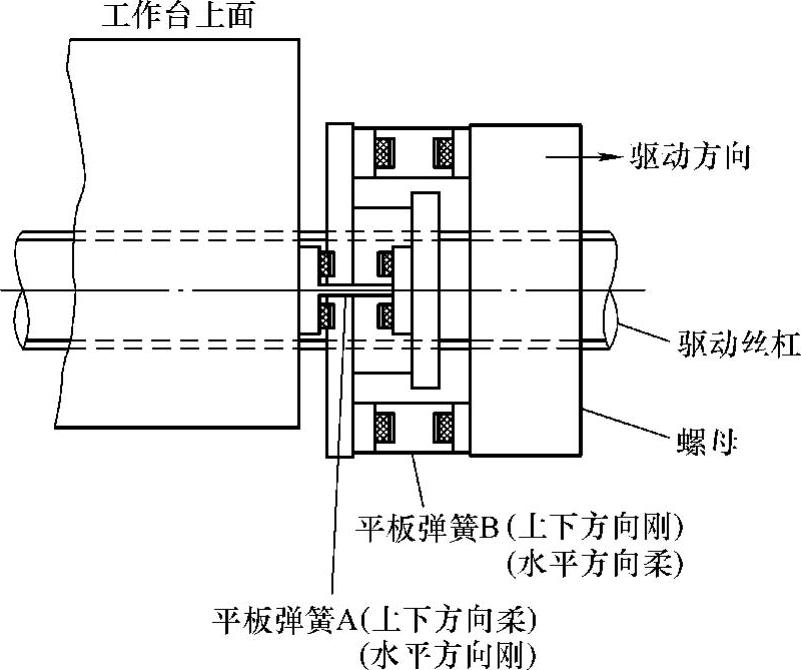
图2.12.5 工作台和螺母之间插入弹簧以吸收丝杠的定位误差

即平板弹簧A在上下方向柔软而水平方向刚硬，平板弹簧B在上下方向刚硬而水平方向柔软。因此，由这样四组平板弹簧的组合在进给方向有刚度能正确地传递丝杠的运动。另一方面，在垂直于进给方向上有柔性，因此可将丝杠和工作台导轨之间的平行度误差吸收，得以实现高精度运动。

【系2】在运动传递要素发生误差时，在该要素的后面插入在误差吸收、除去方向上的低刚度过滤传达要素，以便将误差除去。

此外还有使用弹簧来吸收属于误差的振动的方法，作为主要的形式有振动绝缘和吸振器。振动绝缘与在外部的振动源和高精度机械之间插入误差吸收要素是同一原理。在机械内部本身具有振动源时虽然使用吸振器，但关于吸振器在此不予讨论。在高精度机械内部有振动源，这是本质上的设计错误。此处，只叙述与高精度机械有深度关系的振动绝缘。

如图2.12.6所示，质量为m的高精度机械，假定由刚性为k的弹簧和衰减系数为c的减振阻尼器支承。在支承基础上承受强制变位y，其计算公式为

由于这个输入，作为输出的机械产生了振动，其他静止的平衡点开始的变位x假定为

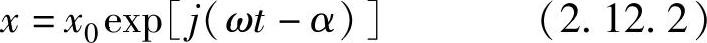
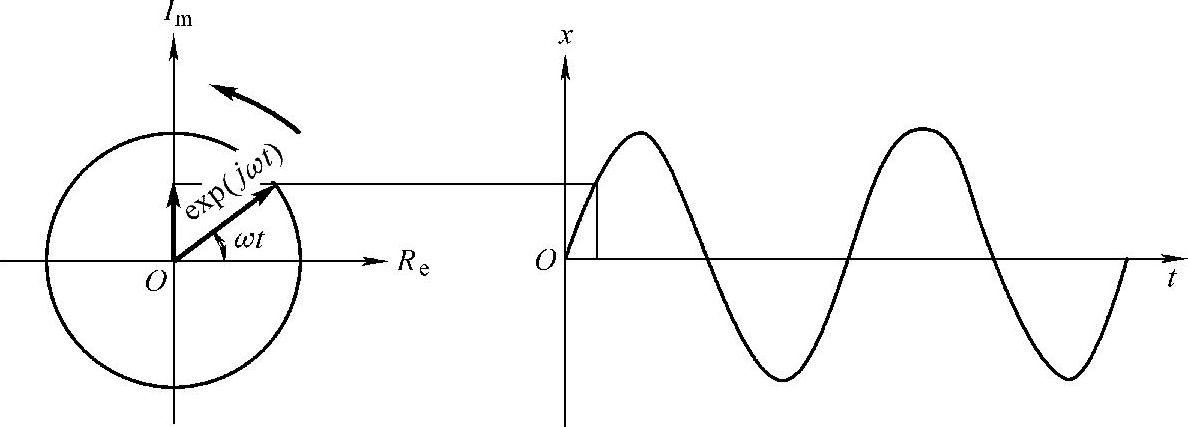
式中，α为对于输入时预先设定的开始状态的相位滞后。这里使用exp（jωt）的函数是根据以下理由：如图2.12.7所示，exp（jωt）函数置于复平面坐标（横轴为实数，纵轴为虚数）上，当时间t从0开始增加以后，表示为长度为1的向量在逆时针旋转时向量尖端的轨迹。

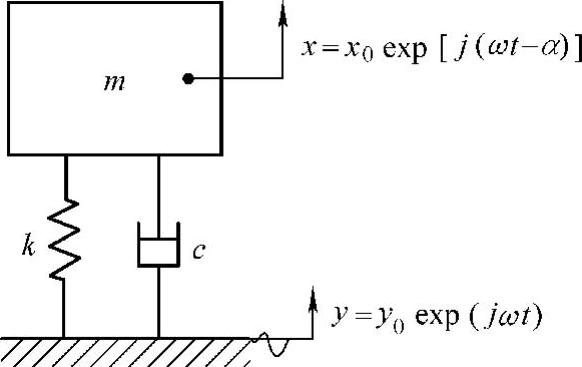
图2.12.6 从外部传入振动时的振动绝缘问题

(www.xing528.com)

图2.12.7 将振动的exp矢量的虚轴（I_m）或实轴（R_e）投影到x轴上表示其与时间的关系

观察一下虚轴上轨迹的投影，投影到时间轴便成为正弦波，正弦波各点对应的时间轴和x轴数值即为exp函数的实部和虚部。表现为实际的振动，把exp视为振动的函数即可。exp是数学上容易使用的函数，因此常用在振动学和电工学上。

在图2.12.6中，外力作用于质量为m的物体上，产生的加速度为x″，运动方程为

整理得

将前面假定的x与y的函数代入，有

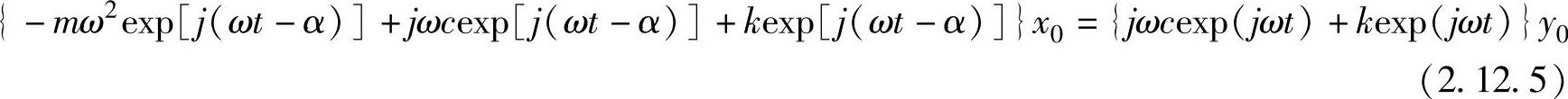
此处，消去左右的exp（jωt），进一步将欧拉公式

代入，左边和右边的实部项、虚部项相等，得

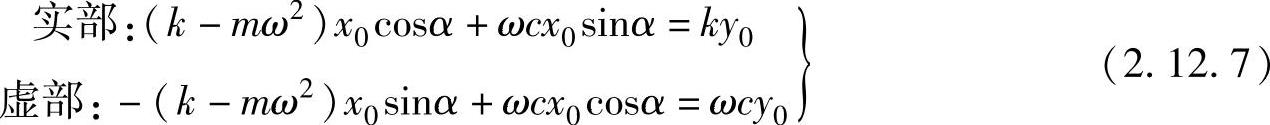
两边平方再相加合成有

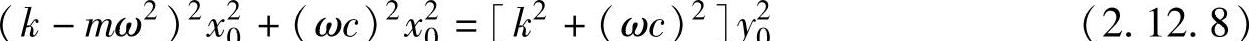
由此得到下式

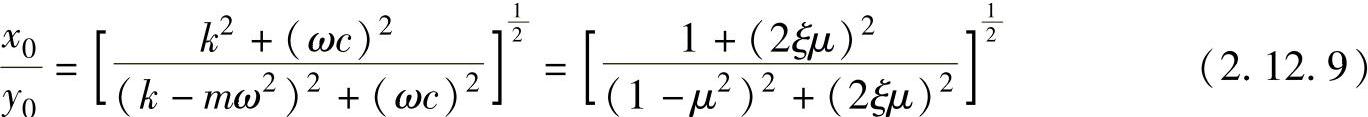
但

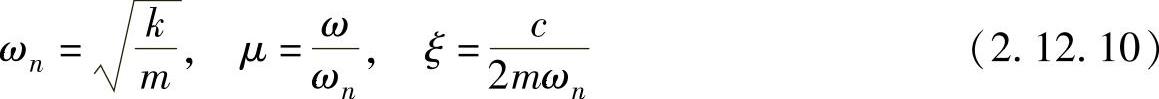
将μ用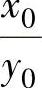图表表示，如图2.12.8所示。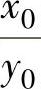（将此称为增益）对于输入的振幅y₀来说，输出的振幅达几倍。μ=1，即引起外部强制变位振动的振动数ω与系统固有振动数ω_n一致时发生共振现象，机器将产生大振动。

为使机器尽量不振动而使其处于静止位置，必须选择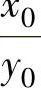为小的支持条件。为此，μ应该在大范围的条件下设计，ω_n（固有振动数）必须做得比ω（外部振动数）小。为此，如式（2.12.10）中的ω_n定义，必须要使m大，k小。关于衰减系数c（和ξ同样倾向），虽然c小时，则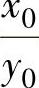也小，但一旦发生振动，例如尽管振幅很小，而其振动却很难抑制，因此必须设计成带有一定程度的衰减作用才行。

【系3】如果该机械由刚性低的过滤要素来支持，则在一定程度上可以吸收、除去来自外部的振动。

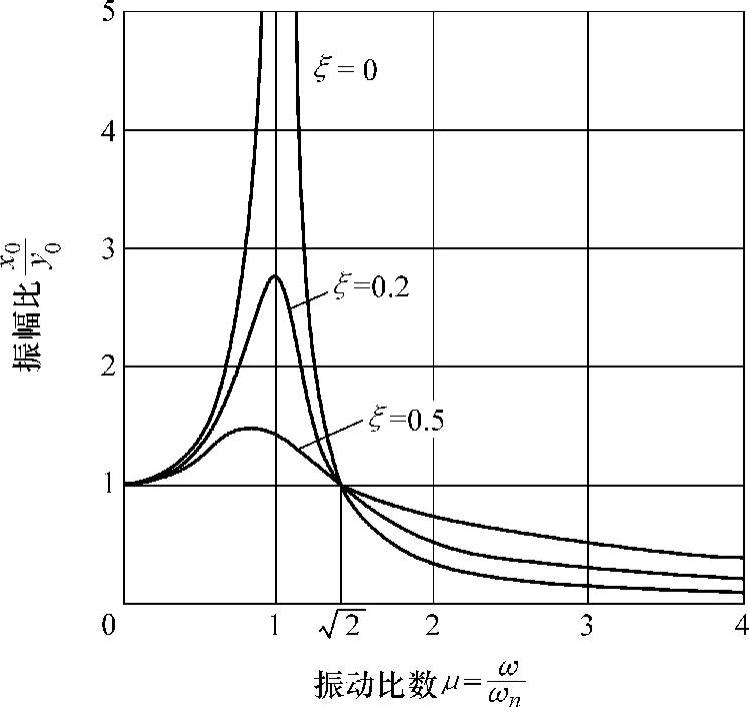
图2.12.8 振动数比μ与干扰振幅y₀对机械振幅x₀的比之间的关系