提高轮廓精度的电流反馈补偿回路控制策略

上面讲到取一圈传达函数的增益在不引起系统的不稳定的范围内以大为好。这里，讲一下有关轮廓精度方面必须注意的事项。

经常有这样的情况，使工作台做描绘平面内作为目标轮廓的运动。下面叙述此时的轮廓精度。

例如，同时控制x和y轴方向使工作台沿某轮廓运动时，如图2.11.11（只表示x轴）所示一般将各轴作为伺服系统来设计。这里采用电流反馈补偿回路（内有速度控制部分）控制较好，因为与轮廓精度没有直接关系，故加以省略。控制系统里的位置控制偏差e定义为

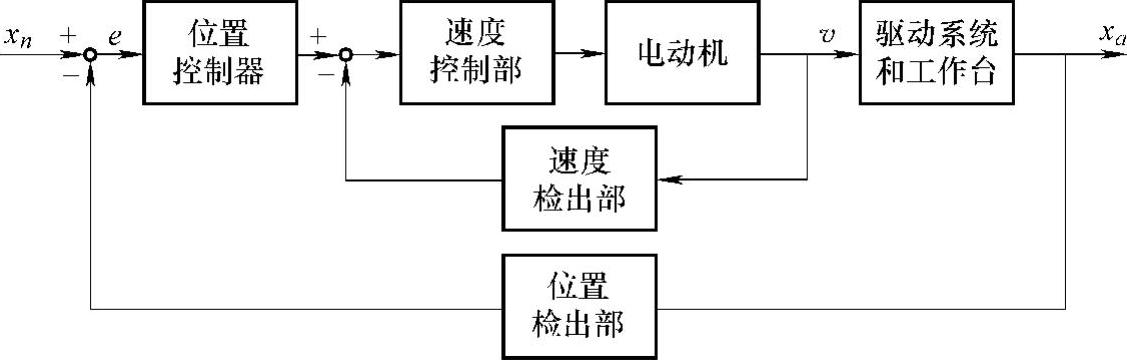
图2.11.11 工作台驱动机构的控制方框图

e=x_n-x_a（2.11.19）

式中，x_n为指令值；x_a为实际的输出。

一方面，与轮廓精度有关的每时每刻的运动方向，由当时两轴的运动速度合成而来。现将v作为实际运动速度，位置的控制偏差为e，速度v的增益K_v（在图2.11.11中，相当于从位置控制部分的输入开始到电动机输出之间的增益）为

将K_v叫作速度增益，速度增益在轮廓精度上具有重要意义。

现在，研究x和y轴同时控制的情况。各轴每时每刻的误差（与上面的e对应）为e_x、e_y、Kvx^和Kvy为各轴的速度增益，由式（2.11.20）可得

(www.xing528.com)

得到上述的关系，这里

K_vx=K_vy（2.11.22）

由此得出

误差发生的方向和工作台的运动方向一致。因此，与形状有关的误差不容易导致维持相似性的轮廓误差的发生，这个情况请参阅图2.11.12便可明白。就是说，一旦K_vx≠K_vy，虽然直线运动和圆周运动的形状都发生变形了，只要K_vx=K_vy，这个变形就不会发生。

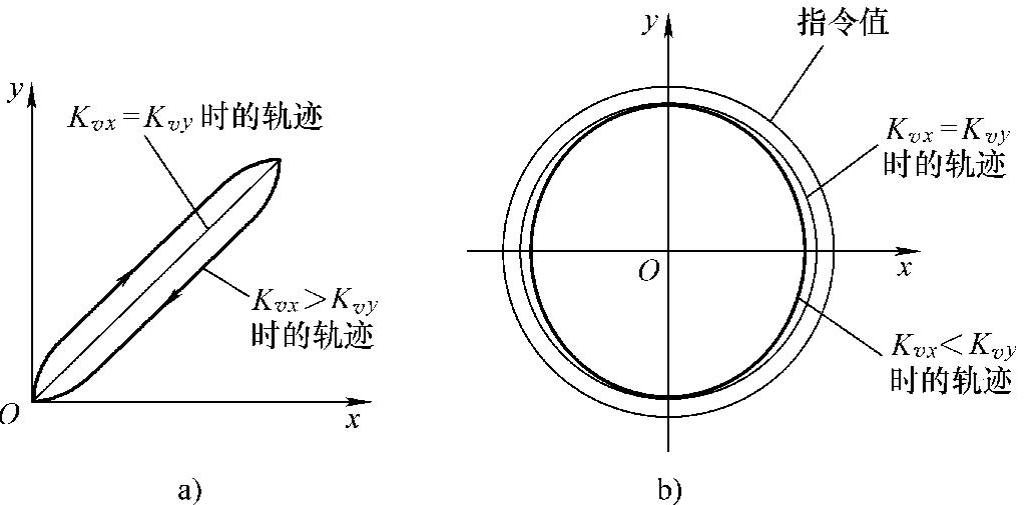
图2.11.12 轮廓误差的发生

a）直线的往复运动 b）圆周运动

当然，即使K_vx=K_vy，如图2.11.12所示那样，仅仅有相当于控制偏差e_i的比指令值为小的圆发生。如系3所叙述，在一个循环里的传达函数必须尽量取高值，根据上述理论得出下面的系4来。

【系4】要提高轮廓精度，必须同时控制轴所有的速度增益。