如何控制误差，保持稳定性？

把数控机床那样的具体控制问题如图2.11.9所示那样做简单的模特置换。首先，对如何缩小干扰影响的方法进行研究。现在，目标值为U（s），干扰为D（s），在图2.11.9a所示的情况下，控制量X_a（s）可表示为

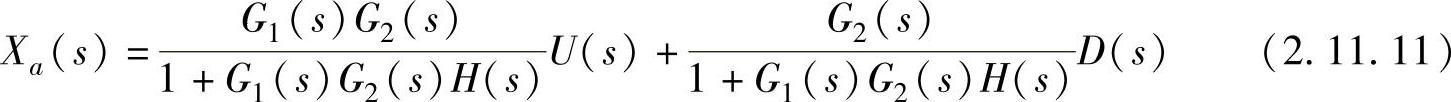
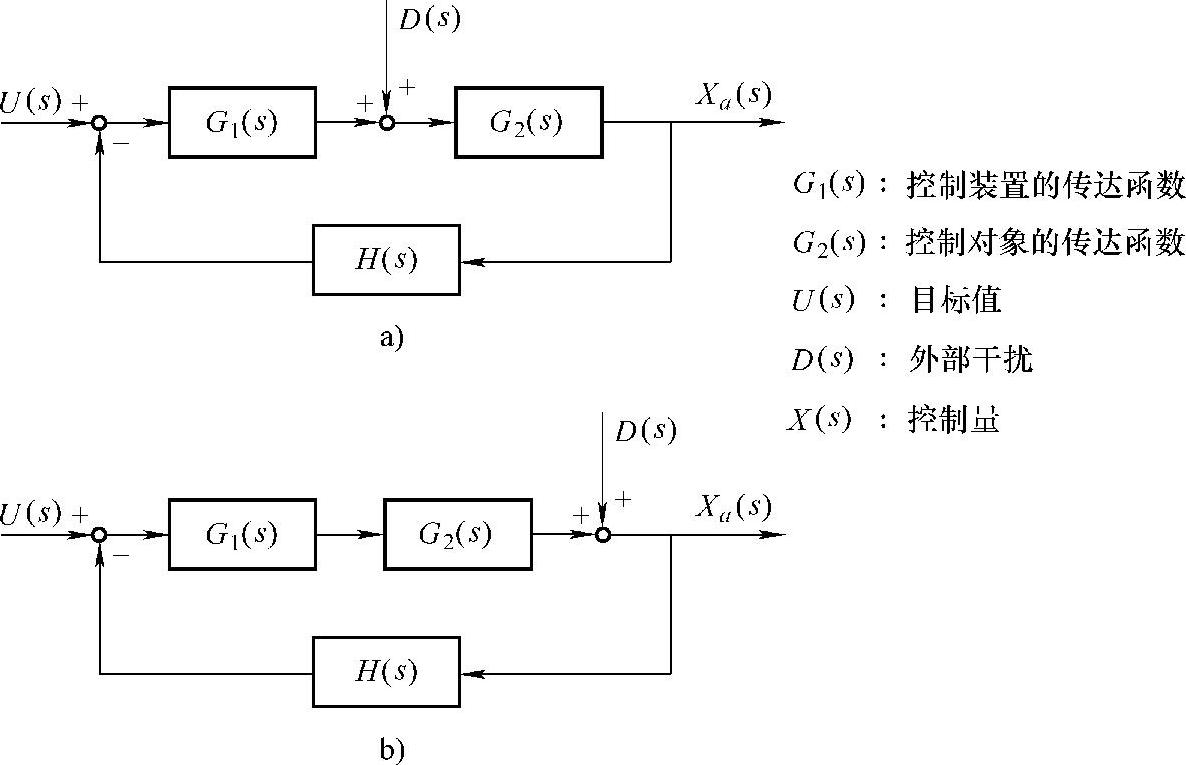
图2.11.9 相对于外部干扰的反馈效果

在图2.11.9b所示的场合，控制量X_b（s）可表示为

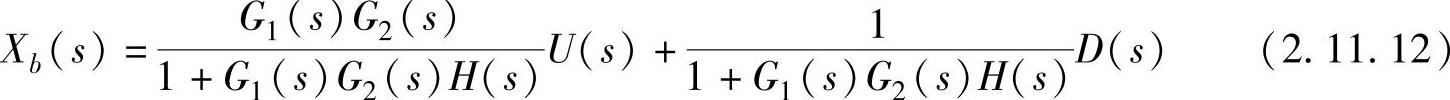
考虑这里决定位置的控制（定值控制的一种）情况，把0作为目标位置时，U（s）=0，上面的控制量各为

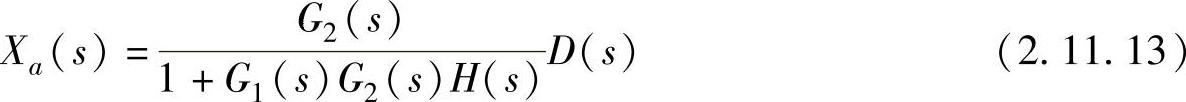
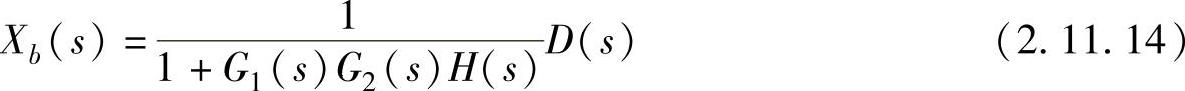
式中的G₁（s）、G₂（s）、H（s）如图2.11.9所表明的那样，是把环的构成要素走一圈而形成传达函数，叫作一圈传达函数。由这两个式子可以明白，要使干扰D（s）的影响小，则必须增大一圈传达函数的值，即必须增大在使用频率范围的增益（下面单纯地叫作一圈传达函数的增益）。进而由以上各式可知，把干扰进入点之前的传达函数，即图2.11.9a中为G₁（s），图2.11.9b中为G₁（s）、G₂（s）的值加大，效果可以提高。

虽然省略详细的说明，但是如果把一圈传达函数的值增大，则即使控制对象的特性G₂（s）发生变化也能够控制控制量X（s）的变动。

还有一个系统组成时的问题，就是定常态的控制量是否与目标一致？把定常态的控制量叫作“定常偏差”。此处把目标值U（s）和控制量X（s）用同一尺度来比较，容易理解一些。如图2.11.10所示，假设H（s）=1的情况来考虑。把目标值U（s）和控制量X（s）的差称为控制偏差，图2.11.10中的控制偏差E（s）由下式赋予：

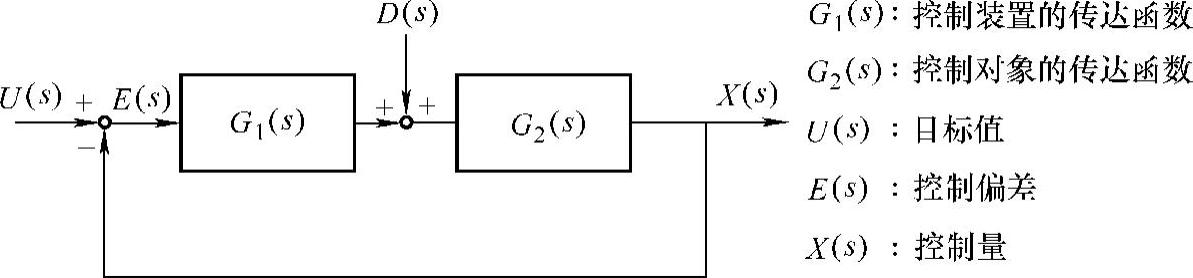
图2.11.10 直接连接反馈控制系统

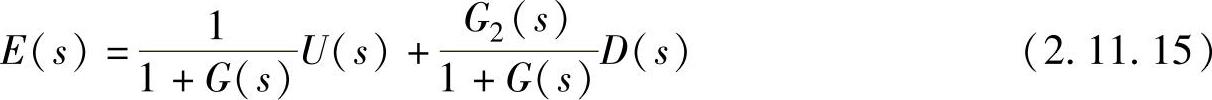(www.xing528.com)

式中，G（s）为G₁（s）G₂（s）时是一圈传达函数。

现在，D（s）=0，则有

进一步，定常偏差e_s由最终值的定理来求出，即

定常偏差是否为零，依存于U和G的形式。

例如，考虑单位一步输入时，U（s）=1/s，由此

如果，G（s）中包含1/s的积分要素，s→0时，G（s）→∞，因此e_s为0，即使e_s不为0，由式（2.11.16）可知，如果一圈传达函数G（s）的增益加大，则可以减小定常偏差。

由上得到，要把控制系统的精度提高，如果把一圈传达函数的增益加大即可，但是另一方面，在反馈控制系统里一圈传达函数的增益太大时，系统会不稳定而发生振动，因此是有限界的。既能保持稳定性而且能控制偏差也小的把相位延迟辅偿要素插入的方法，此处加以省略。

控制系统还有一个重要特性是动特性（追值控制）。针对动特性的基本设计是提高系统的固有振动，对于定速度输入等的定常偏差有必要设计得小些。动特性的问题在此省略。

由以上理论得到下面的系：

【系3】为使在反馈控制系统里受干扰影响小，而且使定常偏差也小，必须在确保系统的定性范围内尽量加大一圈传达函数的增益，欲使干扰的影响小，特别在干扰输入点之前加大传达函数群的增益是有效果的。欲使定常偏差为零，则必须在一圈传达函数中包含积分要素。