掌握曲棍球杆滑动技巧——10.6爬行滑动

由于滑台工作条件不同会发生时进时停的反复细微振动，特别是滑动导轨这样的振动很多。这里叫附着滑动（爬行）。这个振动是一种自励振动。自励振动可以作为具有负的衰减的振动。

如图2.10.9所示，在一个自由度的振动系中衰减系数c为正时，质量m所产生的振动如图2.10.9a所示随时间而衰减，这里阻尼与运动方向相反，产生和运动速度成比例的阻抗而使运动衰减下去。但是在c＜0时，相反地，一旦发生了振动则振动渐渐地加大。即所谓c＜0意味着一旦发生运动，与运动方向相同而与其速度成比例的加速度运动就会发生。即系数的正负决定着自励振动的发生。

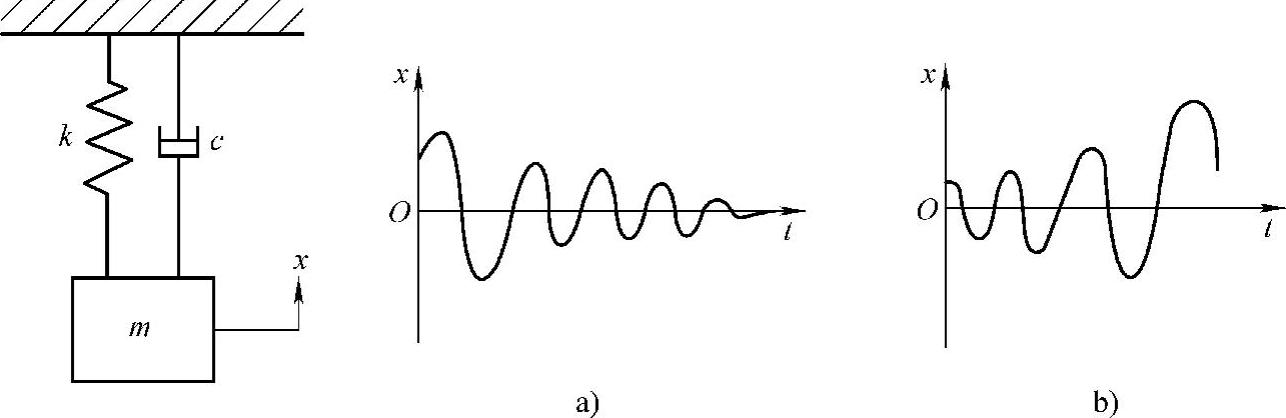
图2.10.9 一个自由度振动系统的衰减振动和自励振动

a）c＞0时（衰减振动） b）c＜0时（自励振动）

这里，先将导轨如图2.10.10所示模型化，滑台由弹簧和阻尼的作用而停止。固定一侧导轨做运动，由于摩擦阻力R而弹簧压缩平衡在某一点，以这点作为坐标原点。

现在，由外力作用滑台以速度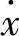向右移动，相对速度为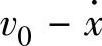，此时，摩擦阻力R如图2.10.11所示变化。以速度为横坐标、摩擦阻力为纵坐标，摩擦特性向右下移。

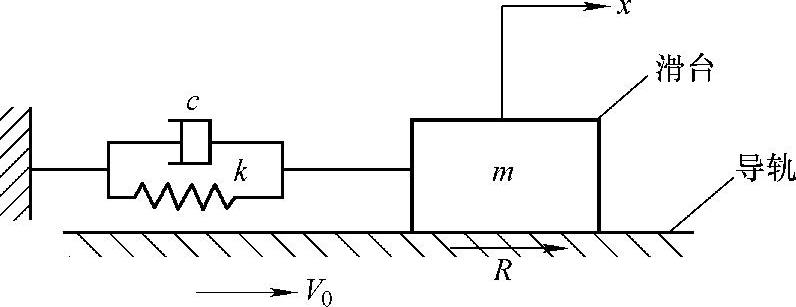
图2.10.10 滑台模型（将滑台静止不动，而驱动导轨运动）

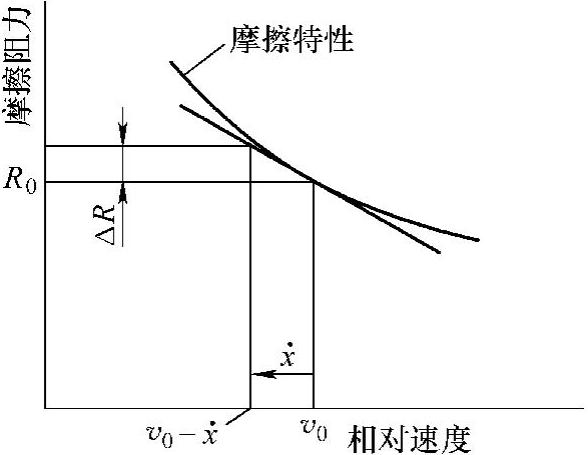
图2.10.11 相对速度与摩擦阻力的关系(www.xing528.com)

相对速度为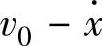时，摩擦阻力增加ΔR，即有函数

此时的运动方程为

因此，用上面的关系式，有

如前所述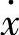的系数为正则稳定，为负则产生自励振动。与此相应地，当c-α＞0时为衰减运动，当c-α＜0时为自励振动，即发生附着滑动。

若图2.10.11中曲线斜率向右上升时，α为负值，c-α为正值，发生的振动必然衰减得到稳定的体系。一般金属做的滑动导轨，如图2.10.11那样具有曲线向右下倾的特性，容易发生爬行，使用聚四氟乙烯、PEEK等润滑性好的材料做的导轨、流体静压导轨等因曲线向右上升而具有避免发生爬行的摩擦特性。

【系5】为防止爬行，导轨面必须使用摩擦特性曲线向右上升的材料。