适用阿贝原理的实例的分析介绍

没有遵守阿贝原理的机械，在我们身边常可看到，例如图2.7.4所示车床刀架的位置。

为了在车床上加工出制品的正确直径，必须正确设定工具刀尖位置。但是，这个工具刀尖的位置由图示手轮和刻度来进行。如图2.7.4中的刻度所示，虽然刻度是环状，但由于其中的线上进给机构，与同一平面内的横向进给工作台可决定位置。因此横向进给工作台的位置决定建立在阿贝原理的基础上。但是，重要的工具尖端的位置从刻度线中心开始仅偏离距离h，因此包括工具在内的工具台的倒角（这个值随横向进给工作台的位置而变动）也会产生误差，其高度方向偏离h成为误差发生的原因。

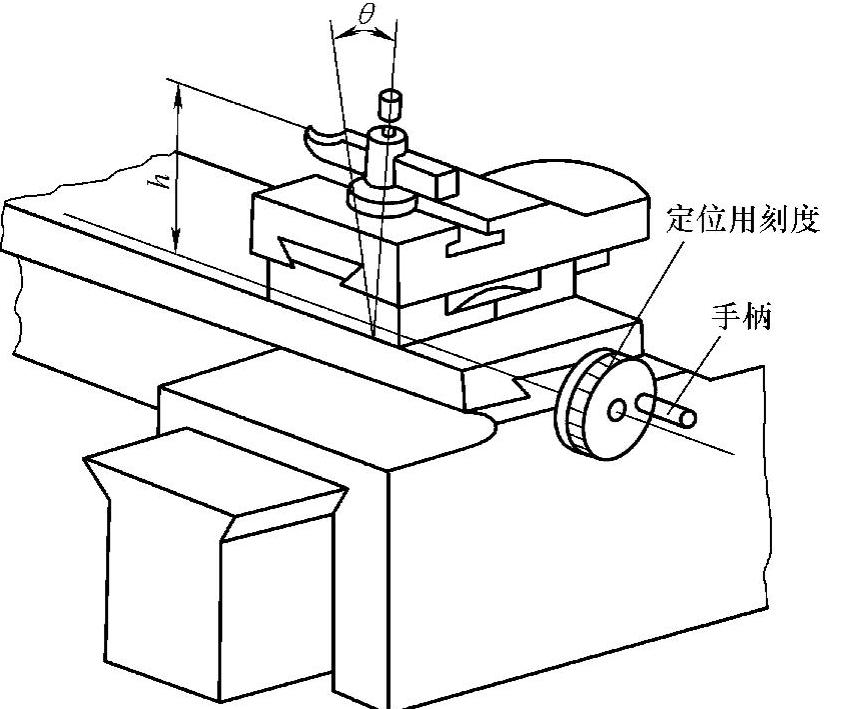
图2.7.4 车床刀架的构造违反阿贝原理

此处，这个构造如图2.7.5所示，做成这样则成了符合阿贝原理的高精度车床。

现实中机械的移动部分只有一根轴是很少的，一般必须沿至少三轴移动，这样一来，1轴可满足阿贝原理，但第2轴以后，满足这个原理则是非常困难的。例如，图2.7.6所示的三次元测定器的代表构造，X轴符合阿贝原理，但由于X轴和Y轴测定长度方向和基准尺的线相偏离，故阿贝原理不成立。因此，在这种情况下应尽可能除去发生的误差或者必须在辅正上下功夫。

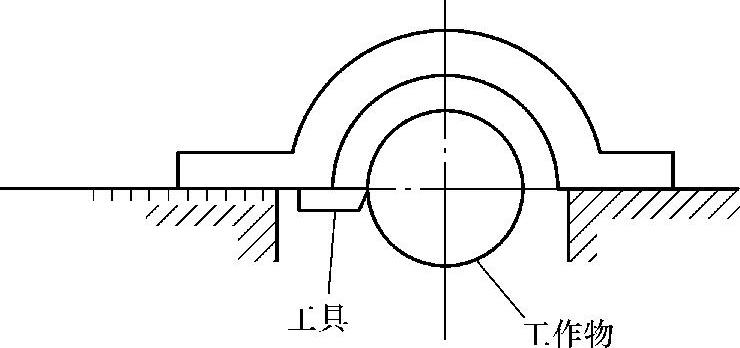
图2.7.5 符合阿贝原理的车床(www.xing528.com)

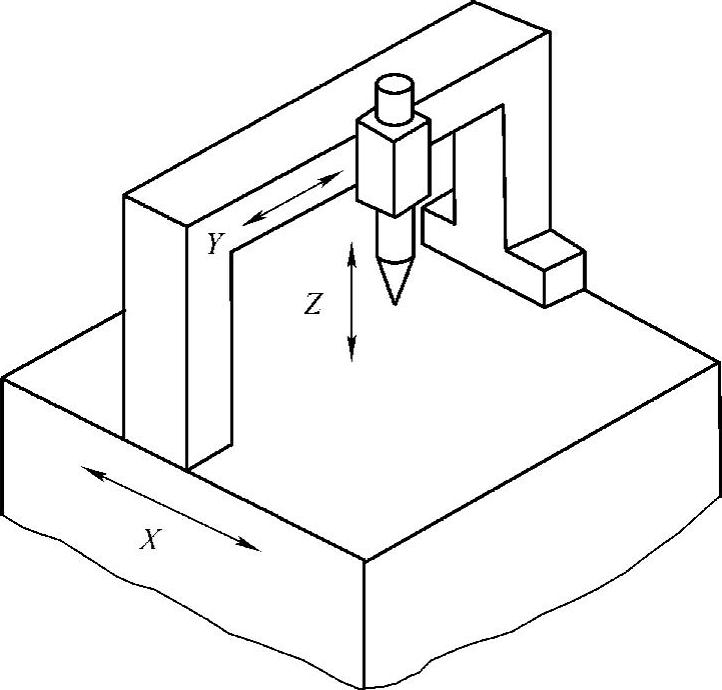
图2.7.6 三次元测定器（很难遵守阿贝原理）

下面的例子是森山等人开发的非轴对称形状的光学零件加工用金刚石自由切割装置。这个机械的关键就是主轴转角及X轴方向的位置决定了正确的工具位置。为此，在其内部设有控制基准的直定规，以此为运动基准，按图2.7.7所示方式控制工具的位置。

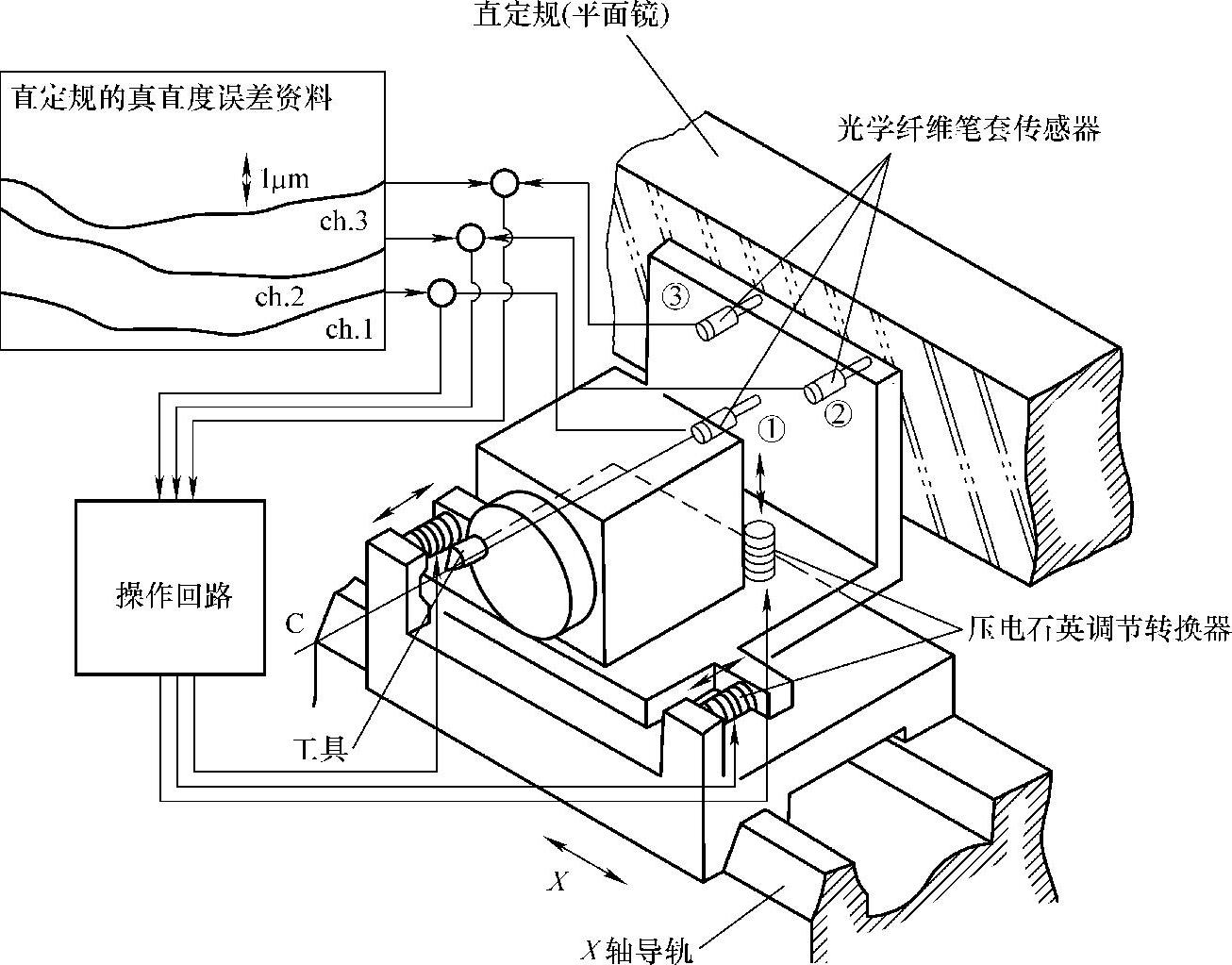
图2.7.7 森山等人开发的非轴对称形状的光学零件加工用金刚石自由切割装置

成为基准的位于工具中心线延长线上的直定规的设置由阿贝原理得以实现。为了实现高精度，这个例子在第2篇第11章叙述的辅正原理中也采用了，在消除直定规的制作误差上也要下功夫。即用纵向主轴台上间隙传感器与直定规对抗，通过其三点信息和预先测定的直定规各位置的误差资料，以及求出支承主轴台三个地方的石英转换器的必要位移量来消除直定规的制作误差。

这个设计欲控制工具的控制轴（与工具的中心轴C在同一直线上）公转移动，因此覆盖其移动范围的领域相对应的三点（①、②、③）的位置作为基准来参照，因而符合阿贝原理。