满足度函数的设计域与信息量限制

根据评价项目的性质，如果信息量不是在系统域范围内，则存在只能赋予一个数值资料的场合。比如，汽车行李箱的大小等评价项目，在系统域里信息量只能赋予一个数值而已，不能进行由概率分布求系统域的操作。

又根据情况可给出范围，但是它的幅度狭窄，实际上与赋予一个数值的状态相同。这时，一般信息量只能是0或∞。信息量为∞，则其系统不能用应将其弃之不用，这时不能比较，而变成消去法。

但是信息量即使变成∞，也常有阻力抵抗从而需放弃此方案。

这样感觉的一个原因是在设计域里面有不确定的因素。设计域绝对不可能实现时，再一次对设计域加以纠正，例如，有必要稍许降低要求进行计算式的纠正。

设计域不是绝对的，加上作为对象的系统的信息量限制在某个数值，如果想在比较中留有信息量的时候，还有一个方法，就是满足度函数（function of satisfaction）。满足度函数和模糊（Fuzzy）理论的全体成员（会员资格）函数形式相同，这里叫作满足度函数。

满足度y取0≤y≤1，1是完全满足状态，0是完全不满足状态。以系统参数为横坐标x，满足度为纵坐标y的坐标平面叫作满足度平面。在这个平面上，以和既定评价项目有关的（x，y）=（x₁，1）点为上端点，以（x，y）=（x₀，0）为下端点绘坐标图，这里将满足度函数定义如下：

【定义7】在满足度平面上连接上端点和下端点的直线叫作满足度函数。

连接上下端点的线，实际上不是直线而是曲线，但为了便于使用在此用直线来表示。把以此为基础只赋予一个数值的参数的系统域像下面那样扩张使用。

满足度函数根据满足的程度也可以引出许多函数。其中在最上侧存在的函数叫上限满足度函数，最下侧存在的函数叫下限满足度函数。试观察一下，如图2.3.5所示汽车行李箱空间的例子。

对于满足度函数的两端，预测参数的最大值和最小值，这样得到的最大值同类点和最小值同类点用两条直线连接，各为下限满足度函数和上限满足度函数。如图2.3.5所示，将某汽车（系统）的空间取为102L，则由横坐标上102数值点的满足度坐标值0.147～0.547对该系统参数赋予满足度的系统域。(www.xing528.com)

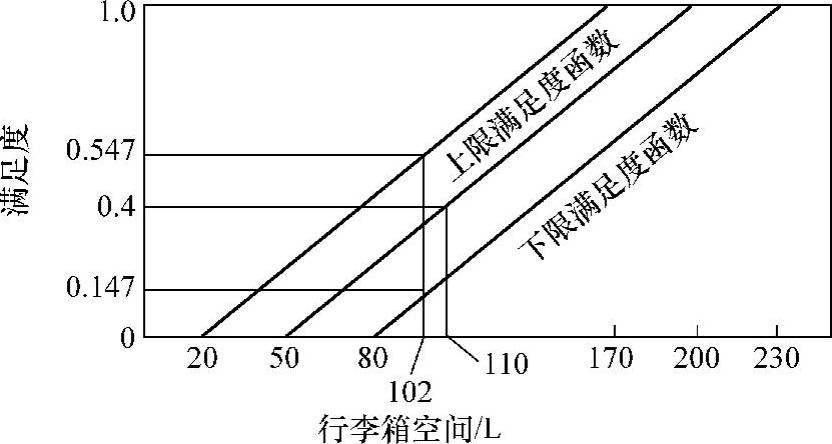
图2.3.5 对于汽车行李箱空间的满足度函数

设计域也同样可以用满足度函数决定，即汽车行李箱欲要有更大的空间值，例如，用平均的满足度函数求对此的满足度，依次为基础决定范围。这时，如果想要110L以上的空间值，设计域的满足度在0.4以上可以决定。

如把上述值移到参数概率密度分布平面，如图2.3.6所示，求与前相同的信息量，即有

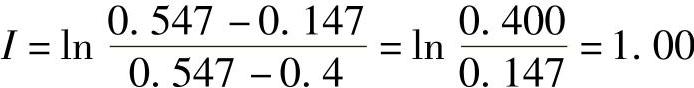
重要的是，关于只给一个数值的评价项目，虽是主观的量，但是变换成满足度这样的量之后，能够决定系统域。

以上所述评价法，不仅在精密机械工程学中可用，在所有领域都可用。用这样的评价法进行高精度机械的设计和加工法的评价，工作得以正确进行。

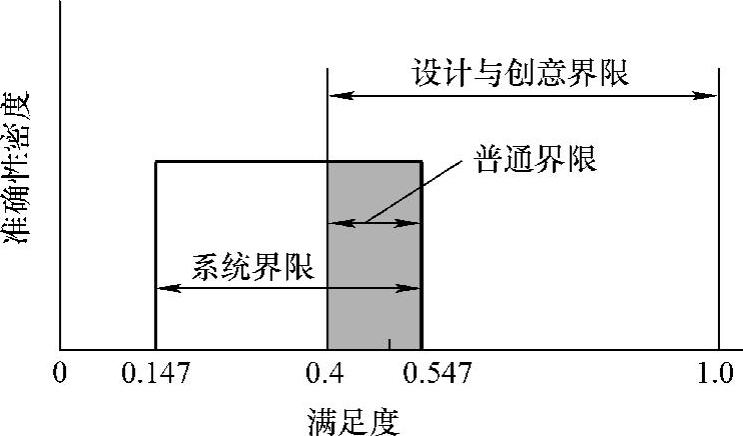
图2.3.6 行李箱的准确性密度分布