信息计算法：基于信息量的评价方法

取代以上过去的不充分的评价法，在新的、综合的、合理的一个公理的基础上的评价法，叫作信息计算法（information integration method）。

一般来说，在系统里欲加以评价的项目，即评价项目有多个，评价项目一经决定，将其加以定量的表现的变量成为必要。

【定义1】代表系统的评价项目的变数叫作系统

参数（system parameter）。

这里，选择某系统参数，当求这个系统实际上取得系统参数值的概率密度分布时，假定如图2.3.3所示，此时，在系统界限l₁的范围内，即使对系统参数不加以特别控制也一定可以取得这个范围的值。

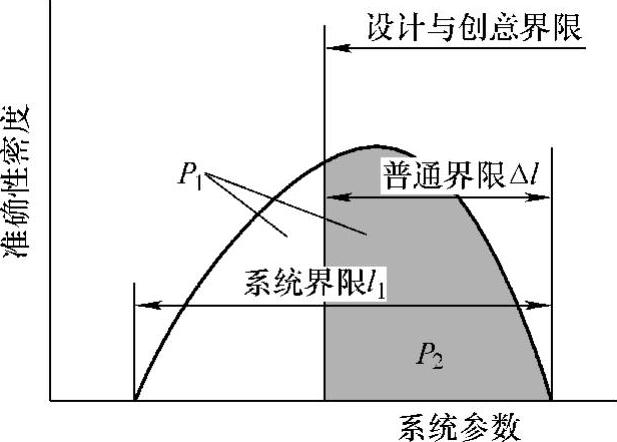
图2.3.3 某系统参数的准确性密度分布

【定义2】系统参数一定取得值的范围，叫作系统域（system range）。

【定义3】系统参数在设计上所要求的范围，叫作设计域（design range）。

【定义4】系统域和设计域相重合的部分叫作共同域（common range）。

在以上准备的基础上，将信息量（information，measure of information）定义为：

【定义5】信息量I为

式中，P₁是取得该系统的相应系统参数的系统域内值的概率（将图示分布曲线内概率密度积分之值），结果为1；P₂为不进行控制，而系统参数取得共同域内的值的概率（同样，将共同域内的概率密度积分之值）。

这样，为了取得系统参数所要范围（共同域）的值，即为了将系统由状态1带到状态2，依式（2.3.1）所计算的相当于I的信息量，必须加入这个系统。

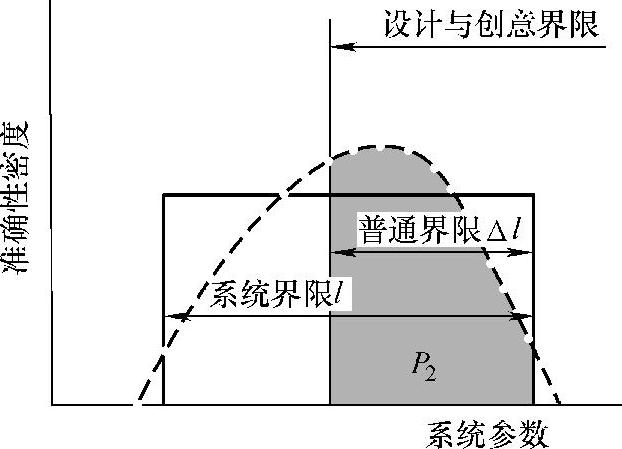
系统参数的实际概率密度分布如图2.3.3所示，严格使用本理论时，将概率分布曲线积分，必须求式（2.3.1）中P₂的数值（概率）。但是实际应用中，尽管不用这样严格的概率密度分布曲线，例如，如图2.3.4那样即使概率密度分布集中而没有问题的场合很多。如果做这样的近似计算而有意义的差不清楚时，必要时用正确的概率密度分布求信息量即可。

式（2.3.1）如图2.3.4所示用均一概率密度分布记号可改写为

(https://www.xing528.com)

图2.3.4 均匀的准确性密度分析情况

这里为了维持被设计系统的状态在所要求的范围（Δl）内，意味着必须赋予称为I的信息量。共同域的幅越窄，式（2.3.2）的分母越小，因此I变大，意味着必须赋予更多的信息量。相反，设计域将系统域完全覆盖了，导致l₁=Δl，I=0，这意味着即使系统不特别给信息量也能达到目的。

再则，这里有信息量I₁、I₂，这两个信息量的和（I₁+I₂）是什么样的信息量，计算如下

则有

P₁₁P₂₁和P₁₂P₂₂是事项1和2复合起来的场合的概率，而且P₁₁P₂₁是两个系统参数1和2取得各自系统域时的复合概率。P₁₂P₂₂是根据赋予的信息量各参数同时取得各自共同域内的值的复合概率。因此，（I₁+I₂）是两个系统参数发生复合时的信息量，往下可得到定理。

【定理1】与各系统参数有关信息量的和，变成这些系统参数发生复合时的信息量（信息量的加法特性）。

这里重要的是，如果将各信息量赋上重要度而相加，那么很快信息量将消失殆尽。例如，将I₁赋予α，I₂赋予β这样的重要度时

P^α₁₁P^β₂₁、P^α₁₂P^β₂₂就不能成为复合事项的概率，因此式（2.3.5）右边的信息量的定义也变得不符合了。

由以上所述可导出以下信息量的定义。

【定义6】合计在系统评价时全评价项目各自所对应信息量得到系统信息量。

这里重要的信息是各评价项目有关的信息量之和，它仍然是信息量，进一步求各信息量之和时不得乘上重要度系数。

现实中，各评价项目间重要度不同，即不能给定评价项目的重要度，将产生各评价项目是否正确的疑问。但是，在信息量中已经包含了实际上相当于重要度的内容。其重要度的不同，与设计域的取法有关，越是重要，设计域严格地被规定，结果信息量增大，其系统参数的影响度也变大。

这里，对于评价提出下面的公理。

【公理1】信息量最小的系统是最好的系统。

这个公理看似很简单，但是对于评价来说有非常重要的意义，是各种重要的概念、方法的源泉，在下面的章节中将加以说明。以这个公理为基础的评价方法，叫作信息计算法。