精密正确，微调至臻 —— 量测优化之道

和“精密量”“精密度”（同为 precision）相似的语言有“正确量”“正确度”（同为 accuracy）和“微细”（fine）。它们在使用中意义经常混同，因此这里把用语的区别叙述一下。

例如：想加工零件尺寸长度为L，用测定器测量全部零件的尺寸，得到图2.1.1所示的结构，一般零件加工以平均值为中心，图2.1.1所示接近于正态分布（一般将其称为t分布，标本数即测定数在30以上时可得到近似的正态分布），这时，将与平均值x^-的指定尺寸偏离值δ_m叫作偏差，这个偏差小的程度叫作“正确量”，又将对平均值的尺寸偏差ε小的程度叫作“精密量”。

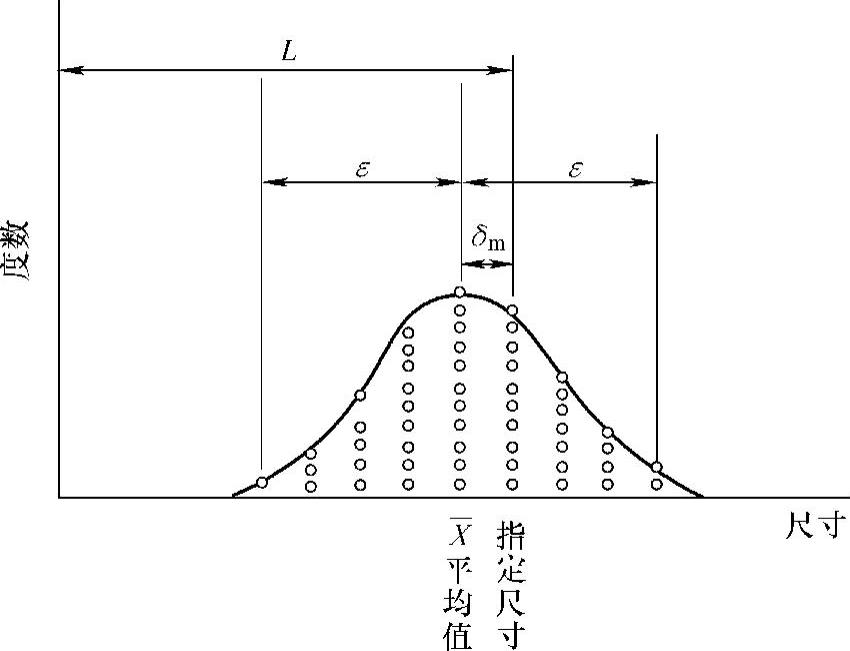
图2.1.1 长度为L的零件加工测定值的度数分布

一般加工也好，测定也好，产生偏差时，将其补正，使x接近于指定的尺寸。但是，由于某种原因而存在无法补正的残留偏差，即产生真正的平均值与指定尺寸（真正的尺寸）的差δ，将它定量地表示即为正确度。当用某种加工法（或测定时）所得到的真正平均值的偏差范围，亦即将正确量予以定量的评价的“正确度”为

这里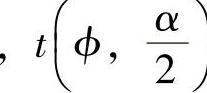是当自由度ϕ=n-1，确率（指在正态分布曲线上，能确定位置的概率）为（1-α）时的t分布值，n为标本数，v为由式2.1.2定义的不偏分散。

举例来说，确率（1-α）一般为95%，叫作“95%的可靠率”。这个场合α=0.05，设n=21（为了易于读t分布表而取作这样的中间数），x=1.5μm，v=4μm²，可查出t（20，0.05/2）的值为2.09，因此由式（2.1.1）可得

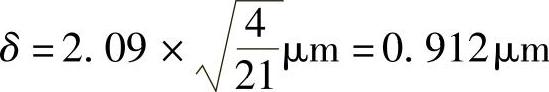
即这个加工法的正确度在0.95的确率和可靠率95%时，大约产生0.912μm的偏差，一般表示写成“0.912μm（95%）”。

另一方面，作为精密量的定量评价的“精密度”定义为(www.xing528.com)

因此，在上面的例子95%的可靠率（α=0.05）时，由于自由度20的t分布值仍为2.09，

因此

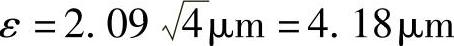
因此，根据这个加工法，得到的结论是，当确率为0.95时精密度为4.18μm，表示成“4.18μm（95%）”。即当确率为0.95时，以平均值x为中心，在±4.18μm的区域内加工尺寸有不均匀偏差存在。

正确度和精密度合起来称为“精度”，误差的极限值的精度τ为

τ=δ+ε（2.1.4）

假定精度充分可靠时，在各种独立变动成分的偏差分散的基础上可以考虑这样来求精度。

接下来讨论“微细”的意义，这与上述的正确量、精密量都无关，总之就是细的意思。例如，沟幅0.1μm也好，10nm也好，都叫作微小的值，这个绝对值有多少偏差不均匀，那不是问题所在。总之，和一般的概念相比是比较小的意思。