基本额定寿命L10h计算法的演变历程

19世纪，通过在自行车上使用轴承，开始普及滚动轴承了，为了减少摩擦，在自行车轮轴心上装入了滚动轴承，这以后，滚动轴承一直得到广泛应用，之所以有这样惊人发展的原因，其中之一是作为设计基础的寿命计算方法长期延续存在。

第一个对滚动轴承的实用寿命进行科学评价的是1881年的赫兹接触理论。20世纪初，休特里别克利用赫兹有关变形和接触应力的理论，求出了滚动轴承的弹性接触变形量。为了求解容许载荷与寿命的判断基准，进行了各种各样的钢材和各种各样的硬度试验，经过不懈的努力，休特里别克测出了纵向弹性系数，以及与之相关的泊松比值0.3，将基于理论的计算值和试验值进行比较，明白了引起塑性变形的接触应力远远小于材料的拉伸应力。

当把远远小于变形极限的载荷即低水平载荷加到滚动轴承上时，轴承的寿命应该有较长的保障，然而，实际上的寿命却因轴承不同而异。虽然能够以不发生塑性变形为条件求出许用最大载荷，却并不能由此预测轴承寿命。

瑞典SKF轴承公司由于其卓越的业绩，在滚动轴承理论、滚动轴承工学、滚动轴承规格等领域，具有指导者地位。阿尔贝德·巴尔姆古连（Palmgren Alvey）构筑了轴承寿命计算的基础，巴尔姆古连出版了《滚动轴承工学的基础（英语版）》一书，很早就论述了L_10h寿命和轴向载荷-径向载荷合成的创意构想。1947年和1952年鲁登别里（Lund Sleeve）和巴尔姆古连（Palmgren）先后联名发表了《滚动轴承的动载荷能力》和《圆柱滚子轴承的动载荷能力》论文，所记载的轴承动载荷能力与寿命计算公式，成为现在L_10h寿命计算公式的基础。

由滚动轴承钢的疲劳强度与威布尔分布的关系，导出了如下公式：

【公式1：能够承受反复变化载荷的概率公式1】

式中 τ₀——最大切应力；

N——在耐受概率S上所能达到的频率；

z₀——最大切应力作用的深度；

V——应力体积的大小。

鲁登别里和巴尔姆古连对函数f（τ₀，N₀，z₀）进行了试验研究，找出了下面的关系：

【公式2：函数1的依存关系】

τ₀^cN^ez₀^-h

此处，指数c、e和h为滚动轴承的常数，取决于轴承。应力体积取决于赫兹接触的宽a、深度z₀和轴承轨道套圈的长度大小L。

【公式3：应力体积】

V≈z₀aL

把公式2与公式3代入公式1，得到公式4：

【公式4：能够承受反复变化的应力耐受概率式2】

可通过公式5计算载荷频率：(www.xing528.com)

【公式5：载荷频率】

当忍耐反复施加载荷的概率S=90%时，得出公式6：

【公式6：反复变化的应力耐受概率S=90%】

切应力τ₀和接触宽度a与最大切应力作用深度z₀完全一样，直接取决于等价载荷P。可以将载荷循环周期数以10⁶为单位来表示，据此导出球轴承的寿命计算公式7：

【公式7：球轴承的寿命函数】

【公式8：L_10h的计算】

由公式7导出

式中 P——轴承的等价载荷（N）；

C——滚动轴承的载荷能力（N）。

球轴承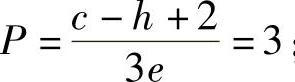：圆柱滚子轴承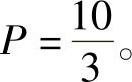

1952年，鲁登别里和巴尔姆古连联名所发表的论文《圆柱滚子轴承的动载荷能力》，后来，这个寿命计算公式被推荐进了国际规格ISO R281。1964年，SKF公司向ISO机构提出了关于轴承的载荷能力（额定载荷）必须改进计算的提议，但是没有马上被接受，ISO直到1969年才开始根据SKF的提议进行改进工作，作为ISO 281/1的古典寿命计算公式如下

此公式后来导入了“修正额定寿命”计算公式，在寿命计算时，可以综合考虑轴承材料、运行条件、长期的润滑等条件，其计算结果的可靠性达90%以上。这样修正的寿命计算公式，在1970年底以DIN ISO 281/-1977的形式被记载下来。

【公式9：修正后的额定寿命计算公式】

式中 L_na——修正额定寿命10⁶转（n表示必要的信赖度和100%信赖度之差）；

a₁——信赖度系数；

a₂——材料系数；

a₃——使用条件系数。