圆柱滚子轴承的纯径向载荷接触面压力与接触区域

轴心线相平行的两个圆筒接触时的接触面压力P_max以及接触面的宽度2b，如图1.8.3所示，根据赫兹方程有

式中，当力单位为N时，A₁=191；当力单位为kgf时，A₁=60.9。

式中 E——纵向弹性系数，材料为钢时，E=

208000MPa或E=21200kgf/mm²；

m——泊松比（对于钢，m=10/3）；

Σρ——两圆筒曲率之和（1/mm），Σρ=

ρⅠ1+ρⅡ1；

ρⅠ1——圆筒Ⅰ（滚柱）的曲率（1/mm），ρⅠ1=2/D_w

ρⅡ1——圆筒Ⅱ（轨道）的曲率（1/mm），ρⅡ1=2/D_i或ρⅡ1=2/D_e

图1.8.3 接触面压P_max和接触面宽2b

D_i为内圈轨道直径，D_e为外圈轨道直径；

Q——加于两圆筒法线方向的负载力（N或kgf）；

L_we——两圆筒的有效长度（mm）。

此处，当力单位为N时，A₂=0.00668；当力单位为kgf时，A₂=0.0209。

当在径向圆柱滚子轴承上施加径向载荷F_r时，最大滚动体载荷Q_max在实际运用中计算公式为

式中 i——滚柱的列数；

Z——每列的滚柱数；

α——接触角（°）。

因此，最大压力P_max及最大载荷加在滚柱与轨道的接触区域时的接触宽度2b计算公式为(https://www.xing528.com)

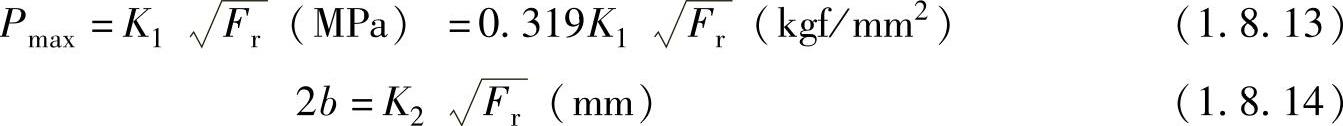
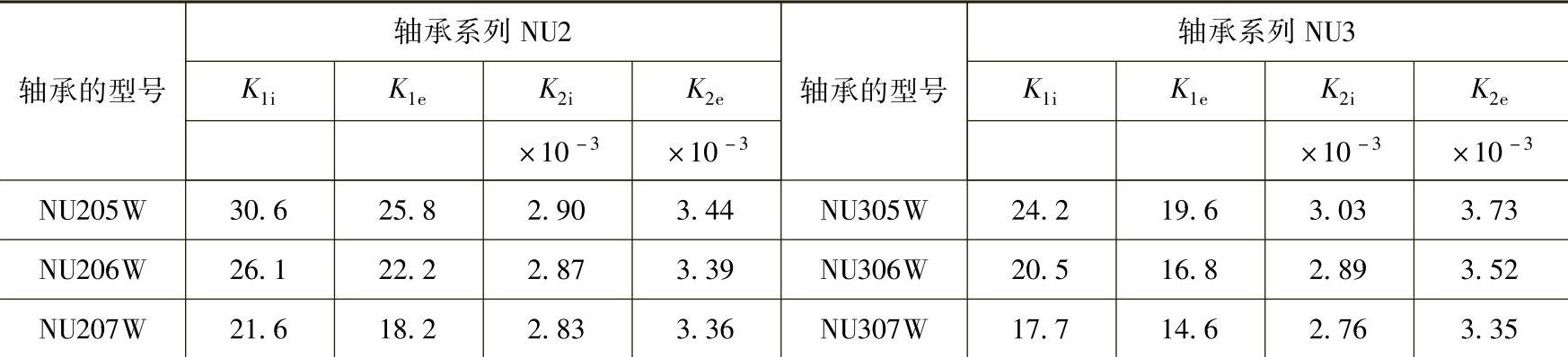
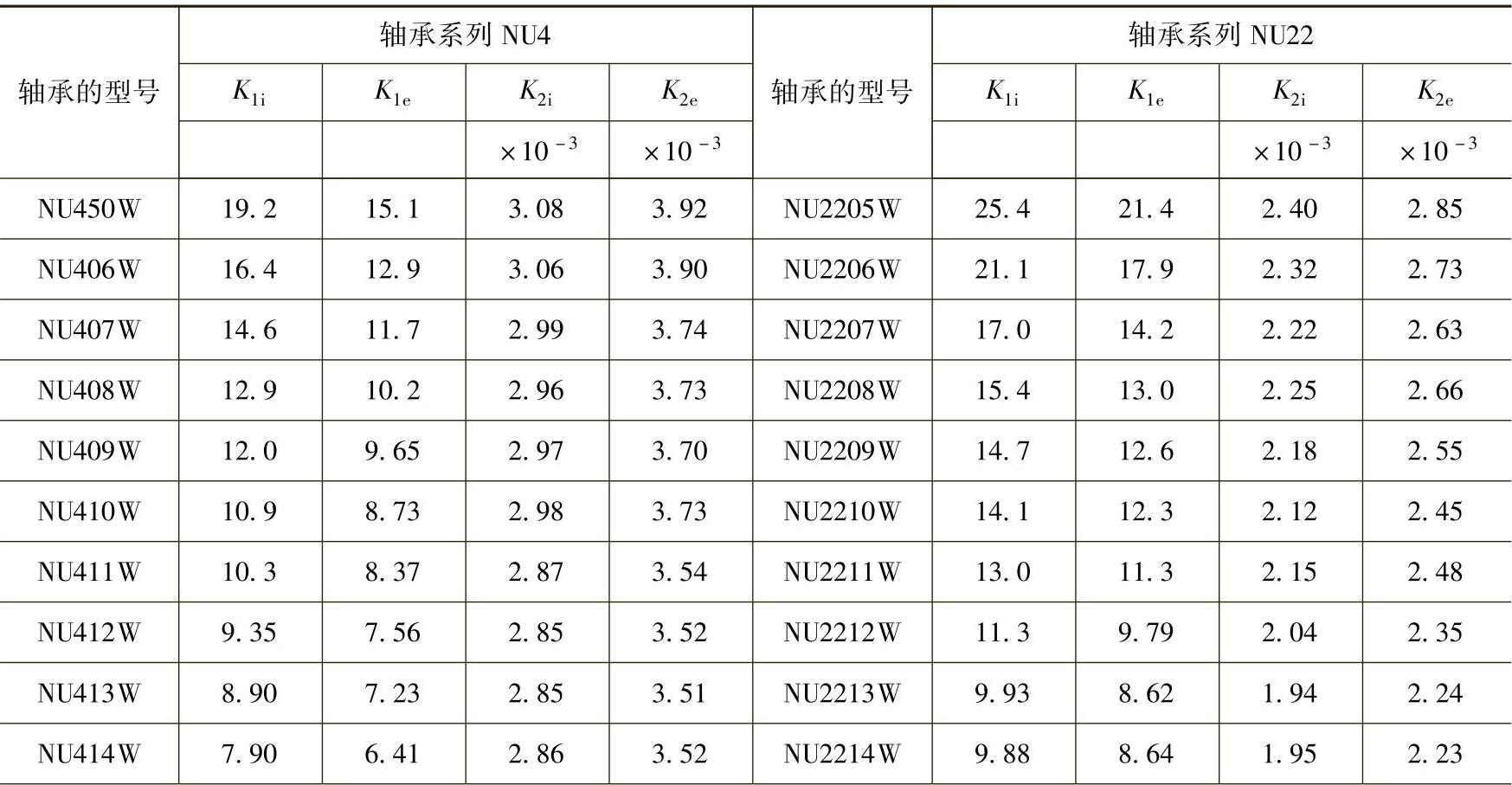
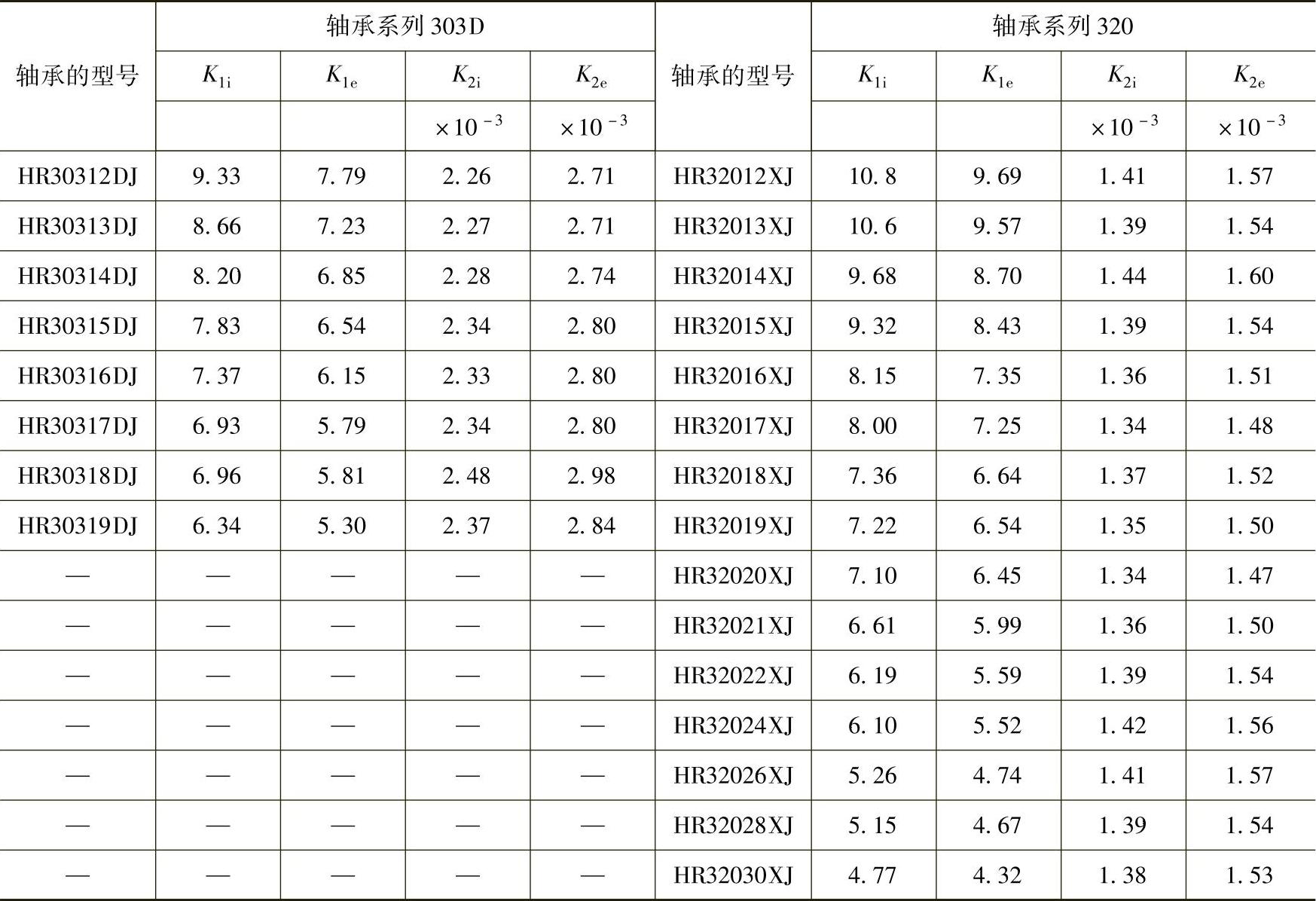
在计算圆柱滚子轴承和圆锥滚子轴承时，常数K₁和K₂的值根据轴承的型号（NSK）从表1.8.2～表1.8.7中查出，K_1i和K_2i是滚柱和内圈接触时的常数，K_1e和K_2e是滚柱和外圈接触时的常数。

表1.8.2 圆柱滚子轴承的常数K_1i、K_1e、K_2i、K_2e值

（续）

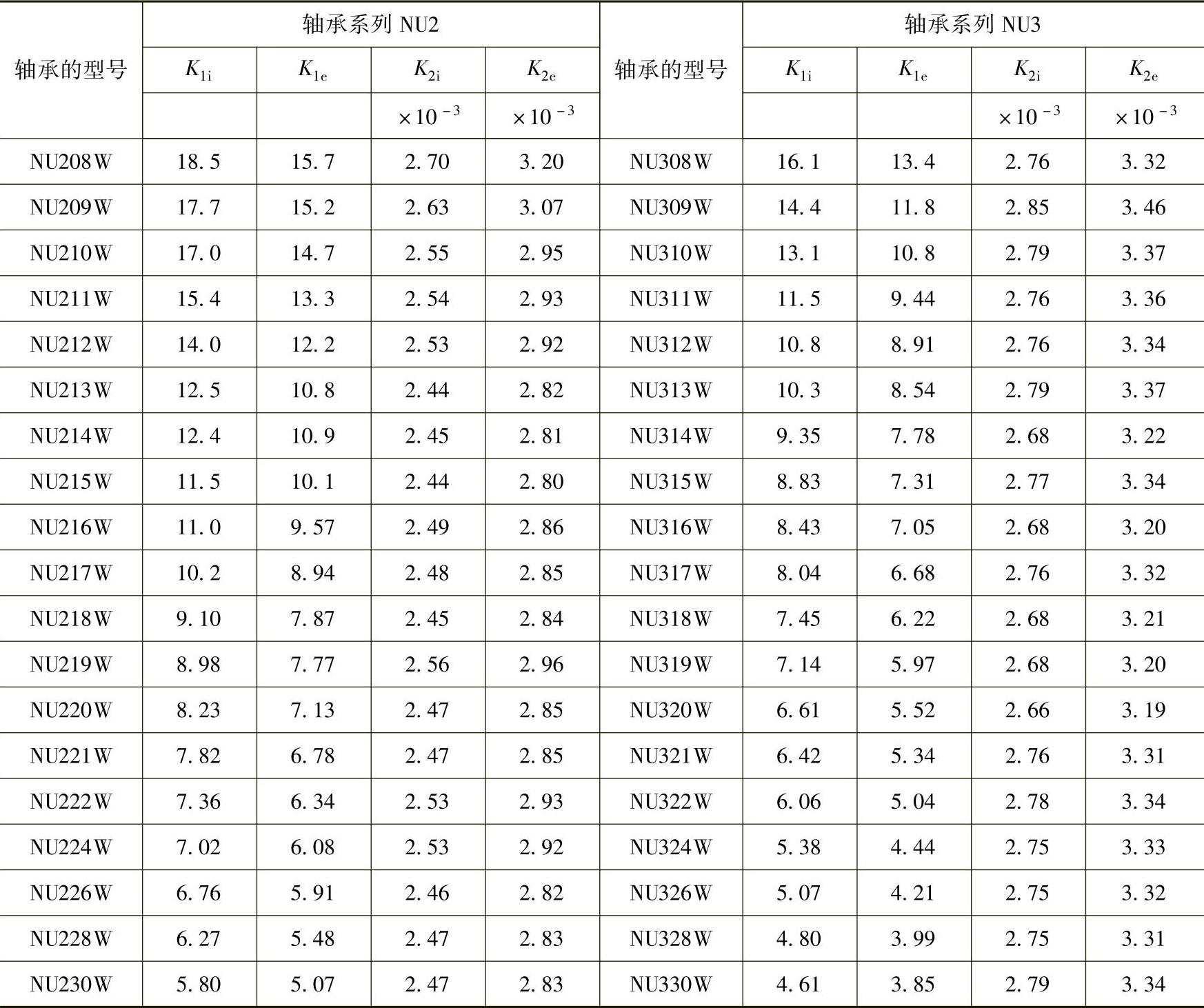
表1.8.3 圆柱滚子轴承的常数K_1i、K_1e、K_2i、K_2e值

（续）

表1.8.4 圆柱滚子轴承的常数K_1i、K_1e、K_2i、K_2e值

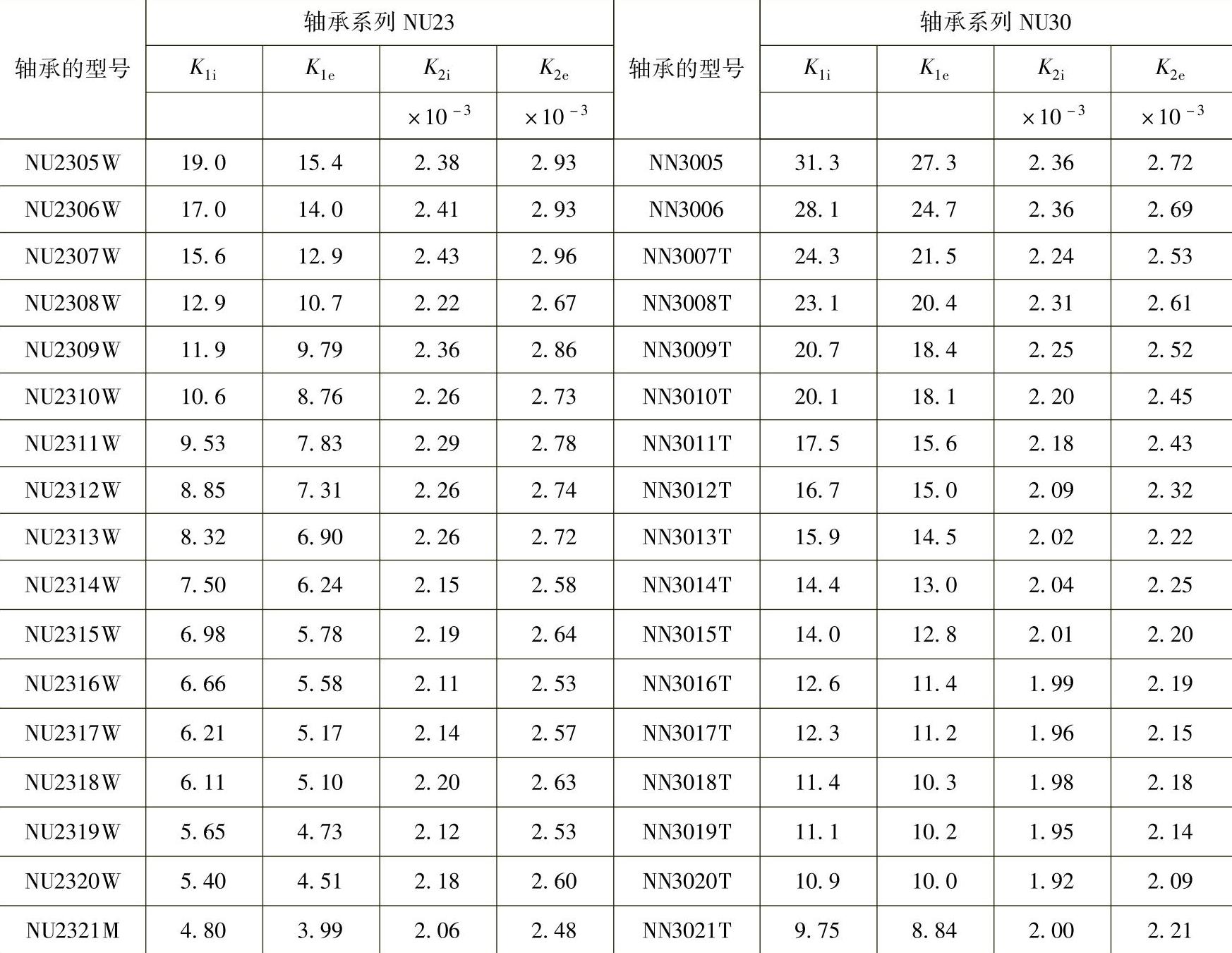
（续）

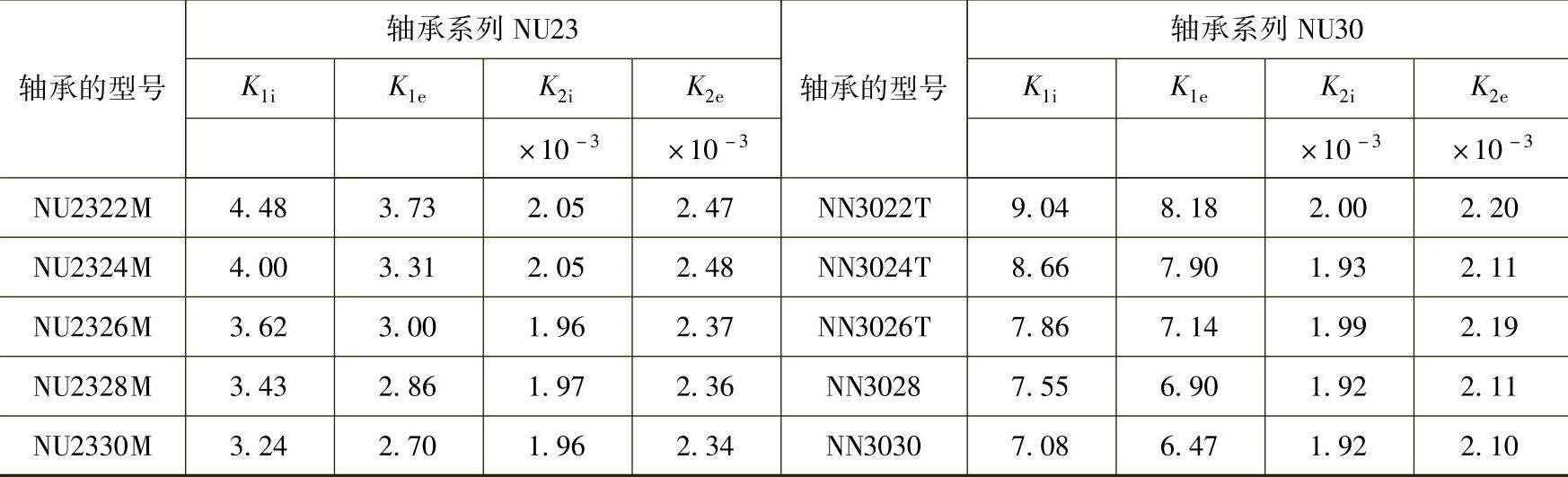
表1.8.5 圆柱滚子轴承的常数K_1i、K_1e、K_2i、K_2e值

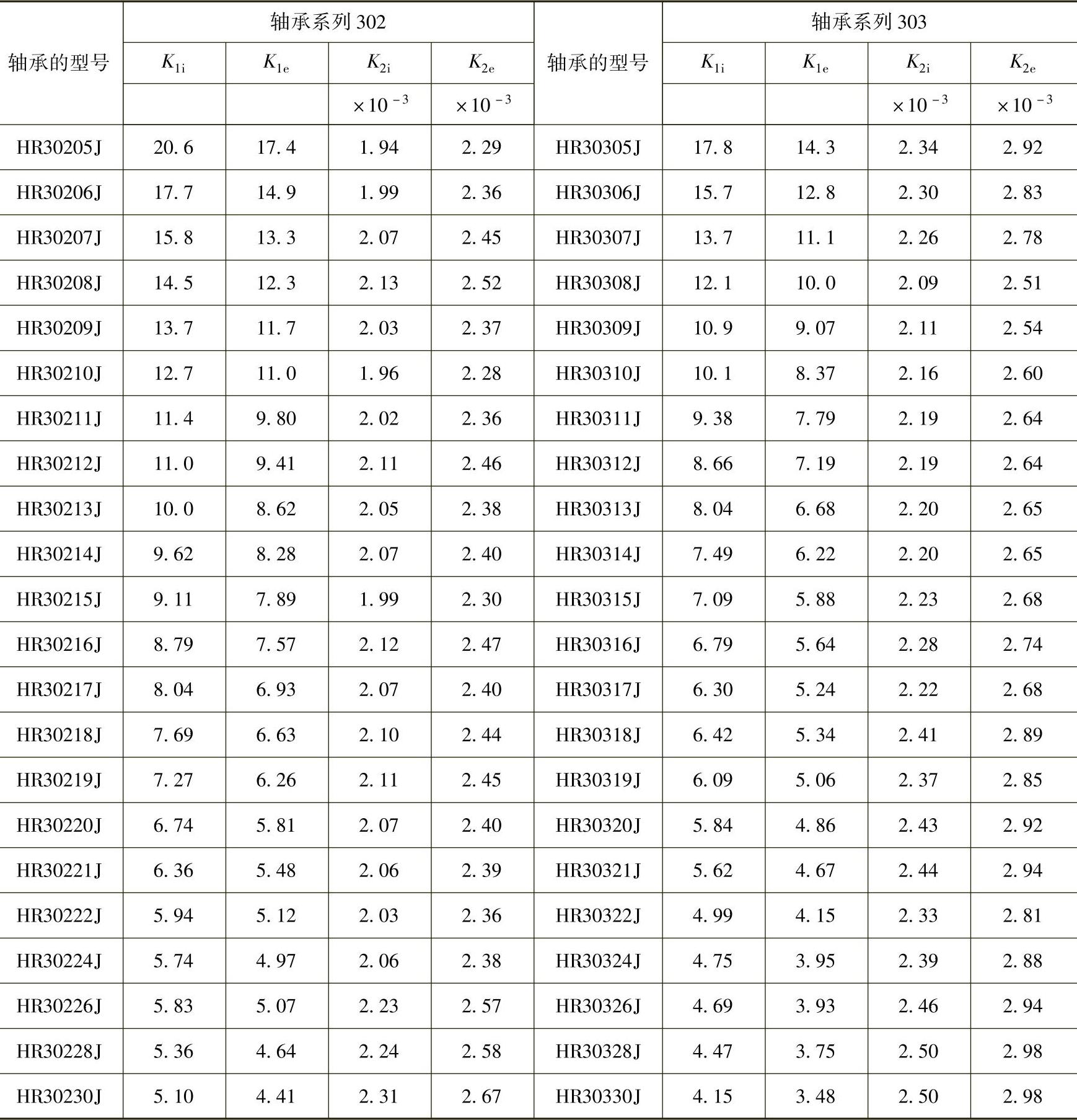
表1.8.6 圆柱滚子轴承的常数K_1i、K_1e、K_2i、K_2e值

表1.8.7 圆柱滚子轴承的常数K_1i、K_1e、K_2i、K_2e值

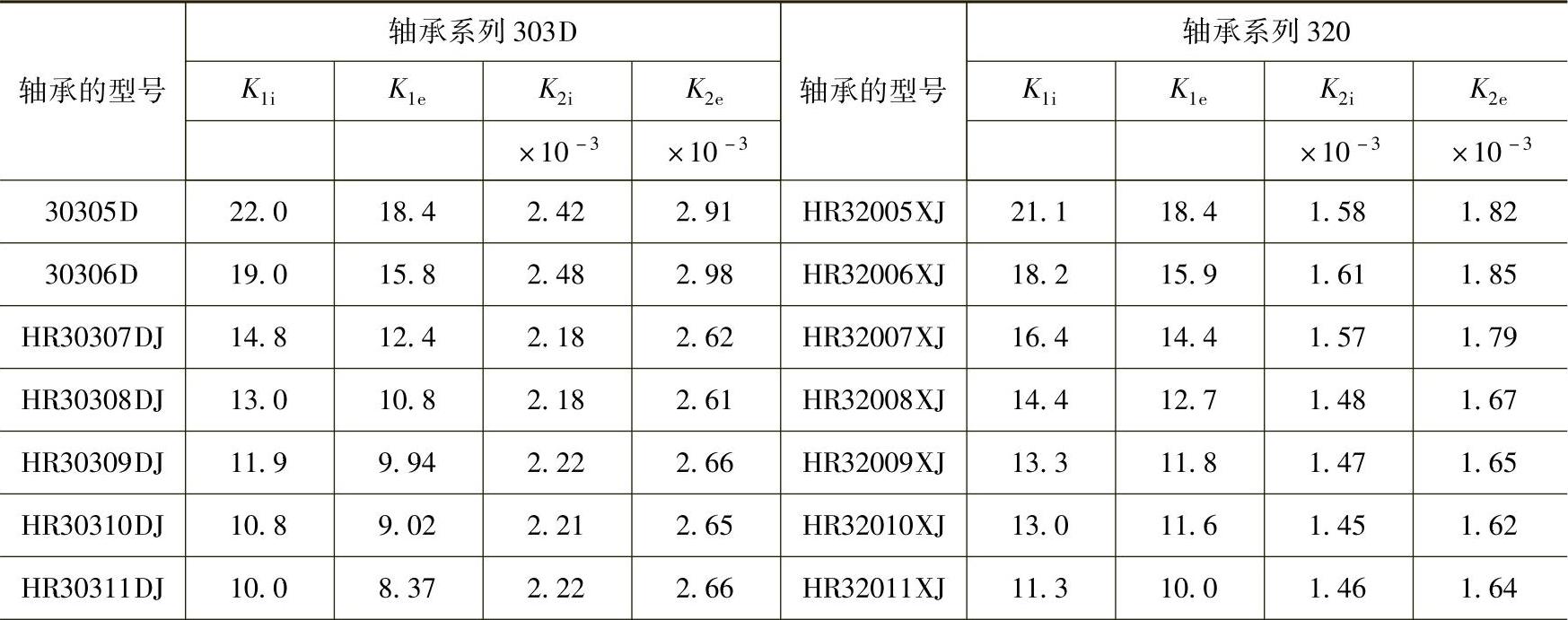
（续）