球轴承中滚动体和轨道圈的接触问题,是一个赫兹理论的典型应用问题,理论和实践结果相当好地进行了对接论证。
一般情况下,内圈滚道较之外圈滚道所承受的接触条件要恶劣一些,载荷压力也大一些,因此讨论集中在内圈上。
如图1.8.1所示,当滚珠与滚道的接触开始承受外力载荷时,原来的点接触就会因载荷而变成弹性圆面接触,系统的间隙由零间隙变成预紧状态的过盈配合,接触轨迹的几何尺寸直接影响滚动轴承的刚度、精密度、噪声和使用寿命等参数。
滚动轴承一旦接受外来载荷,滚珠和轨道的接触区域经弹性变形成椭圆状,令椭圆面所受的最大面压力为Pmax,接触椭圆面长径为2a,短径为2b,根据赫兹方程有
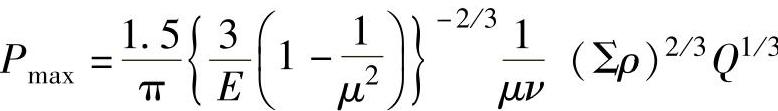
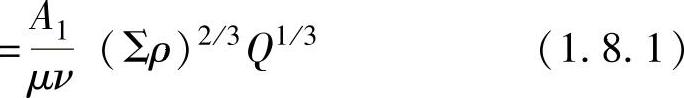
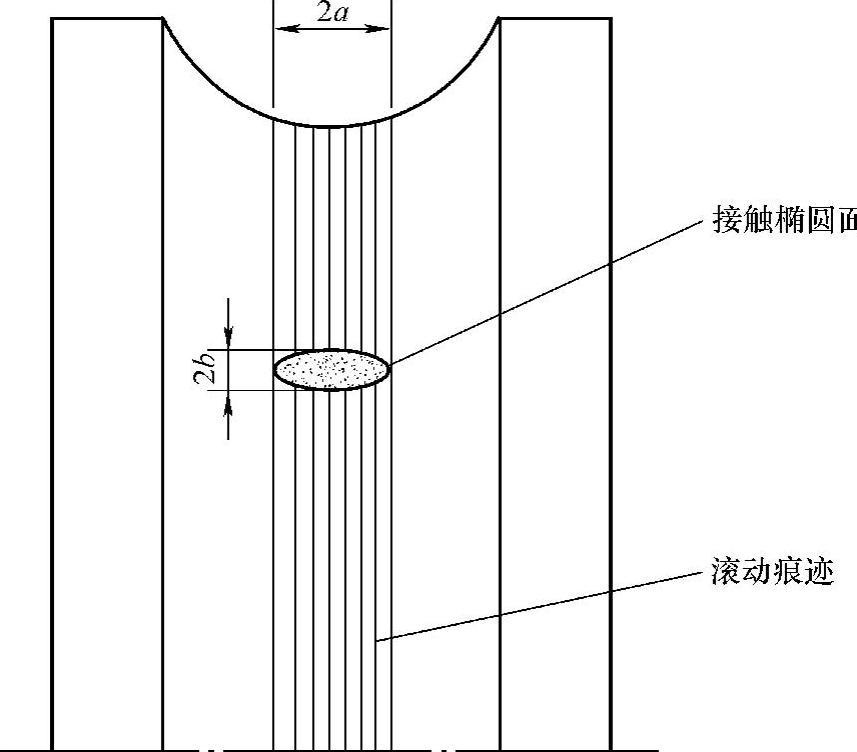
图1.8.1 内圈轨道滚动痕迹(滚动体接触痕迹)
此处,当力单位为N时,取A1=858;当力单位为kgf时,取A1=187。
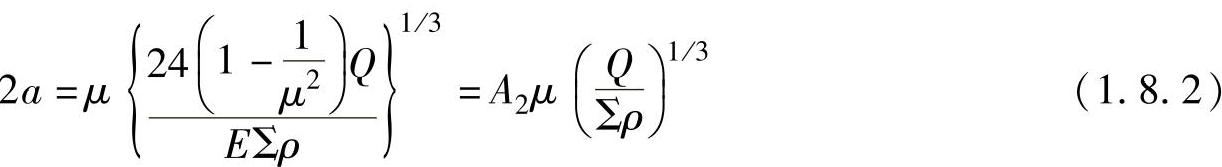
此处,当力单位为N时,取A2=0.0472;当力单位为kgf时,取A2=0.101。

式中 E——纵向弹性系数,材料为钢时,E=208000MPa或E=21200kgf/mm2;
μ——泊松比(对于钢,μ=10/3);
Σρ——主曲率的总和。
径向球轴承为

式中 Dw——滚珠直径(mm);
f——滚道圆弧半径与滚珠直径之比;(https://www.xing528.com)
γ——γ=Dwcosα/Dpw;
α——接触角(°);
Dpw——滚珠的分度圆直径(mm)。μ、ν由式(1.8.5)的cosτ值作为参数,在图1.8.2里查出。

径向载荷Fr加在球轴承上所产生的最大滚动体载荷为Qmax,滚珠数量为Z,在实际运用中,式(1.8.6)表示Fr、Qmax和Z的关系:
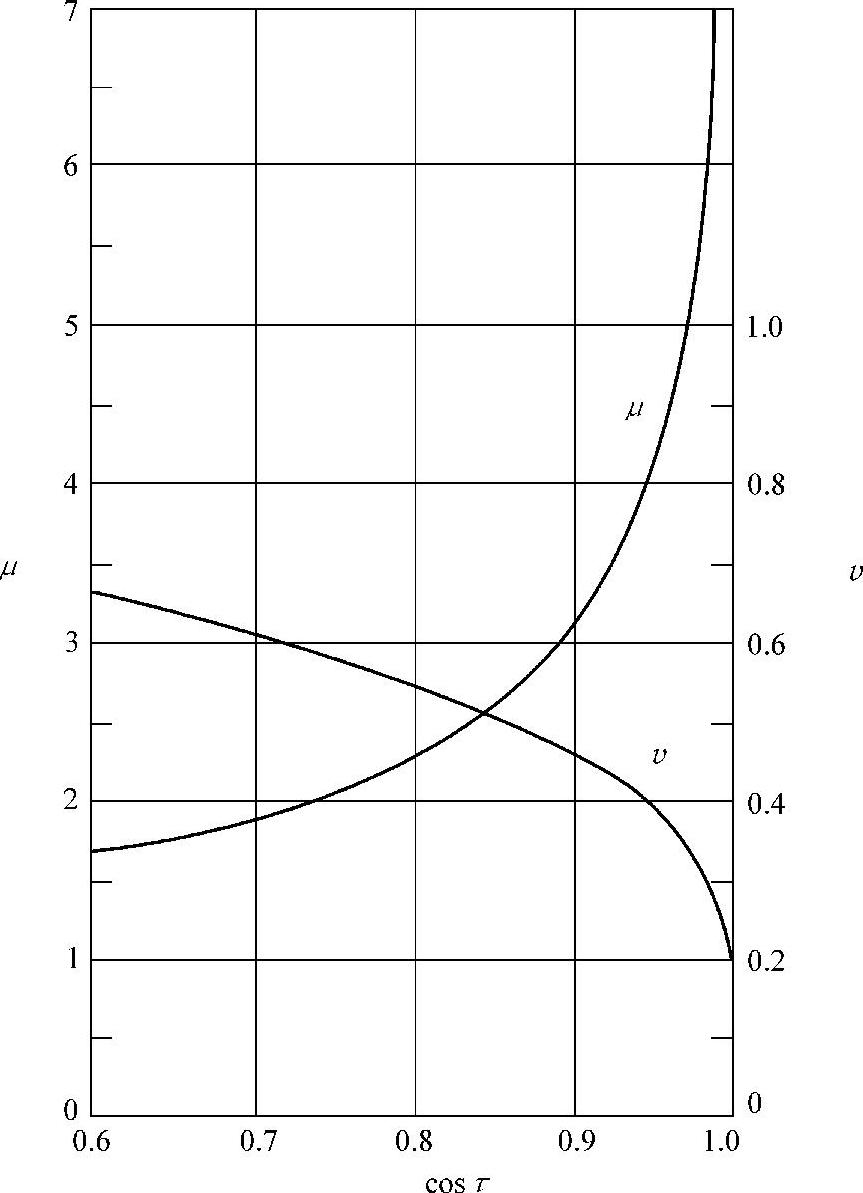
图1.8.2 由cosτ求μ、ν的值

因此,将式(1.8.4)、式(1.8.6)代入式(1.8.1)、式(1.8.2)、式(1.8.3)有

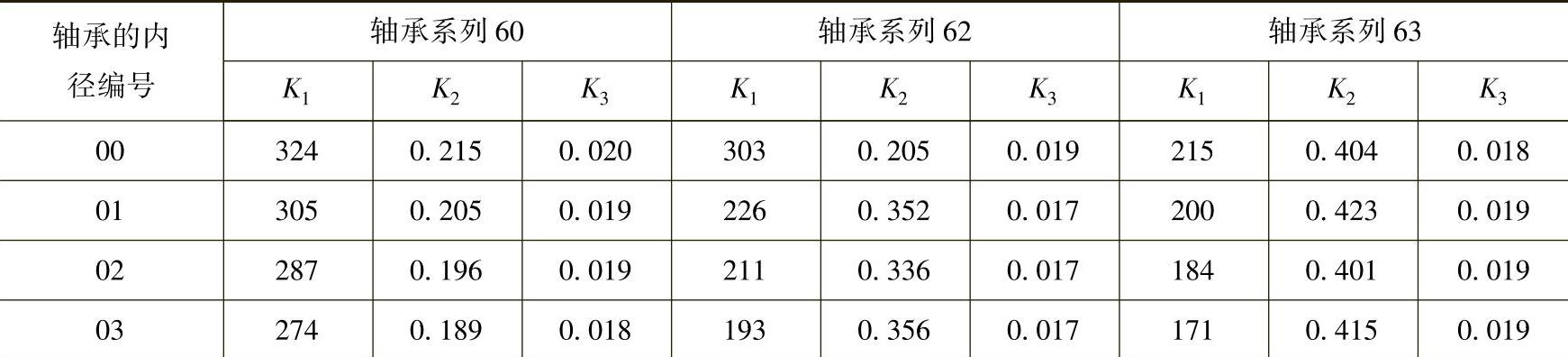
深沟球轴承的常数K1、K2、K3值见表1.8.1。
例 深沟球轴承6210承载载荷为纯径向载荷Fr=3500N(基本额定动载荷的10%),求此时的最大面压和滚珠和内圈外轨道之间的接触面尺寸2a、2b。
表1.8.1 深沟球轴承的常数K1、K2、K3值
(续)
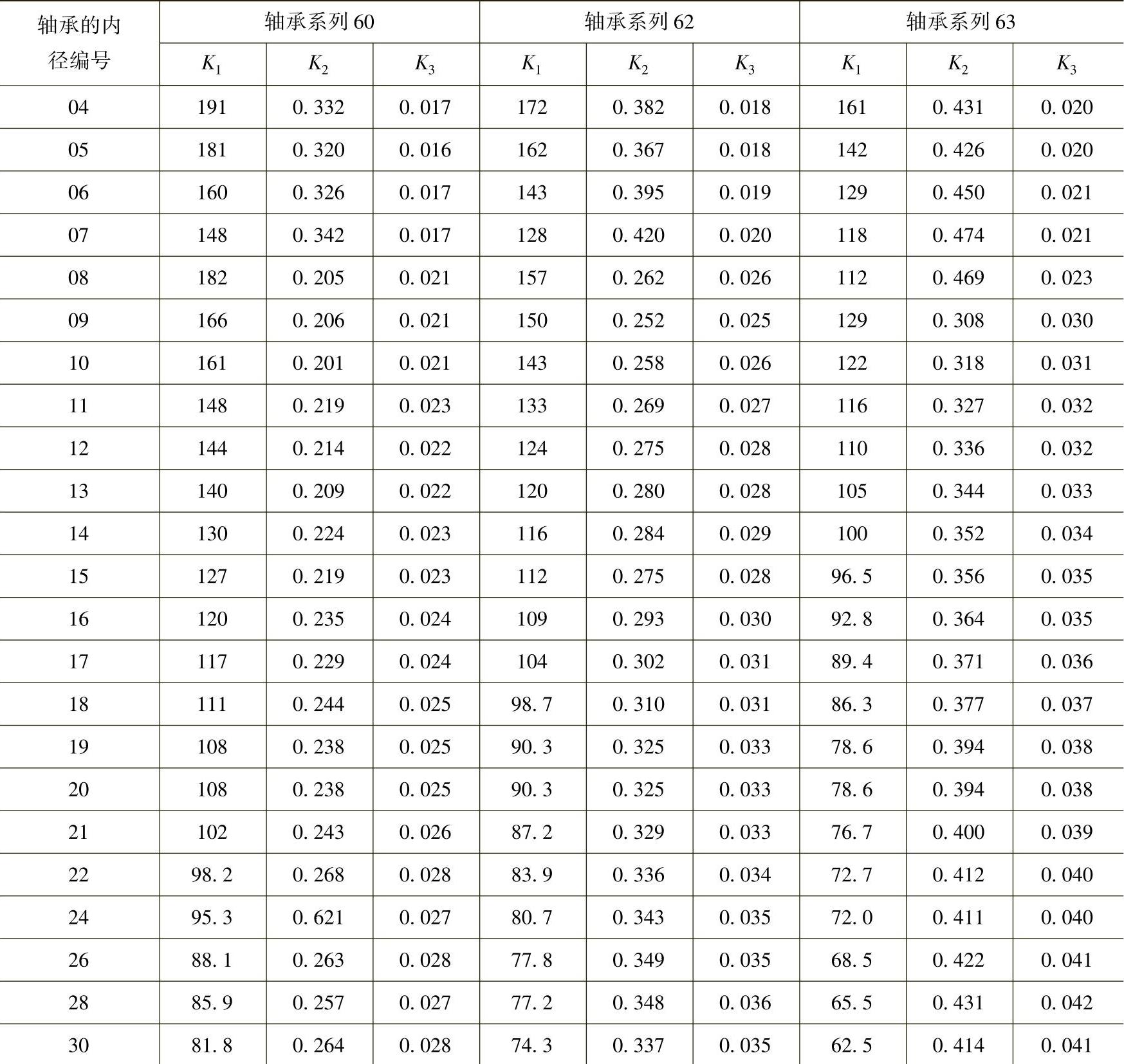
从表1.8.1中查出K1、K2、K3值,有下述计算结果:
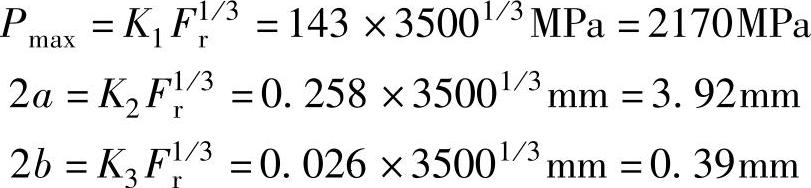
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




