曲面体接触应力分析

（1）坐标系 图1.7.2所示为一曲面体的一部分，它在E点与另外一曲面体相接触，E点称为初始接触点。取曲面在E点的法线为z轴，包括z轴可以有无限多个剖切平面，每个剖切平面与曲面相交，其交线为一条平面曲线，每条平面曲线在E点有一个曲率半径。一般不同剖切平面上的平面曲线在E点的曲率半径是不相等的。这些曲率半径中，有一个最大和最小的曲率半径，称之为主曲率半径，分别用R′和R表示，这两个曲率半径是相互垂直的。平面曲线AEB所在的平面为yz平面，由此得出坐标轴x和y的位置。任何相接触的曲面都可以用这种方法来确定坐标系。由于z轴是法线方向，所以两曲面在E点接触时，z轴是相互重合的，而x₁轴和x₂轴之间、y₁轴和y₂轴之间的夹角用ϕ表示，如图1.7.3所示。

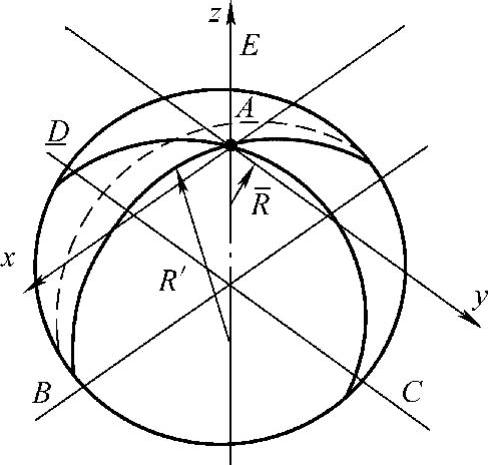
图1.7.2 曲面体的坐标

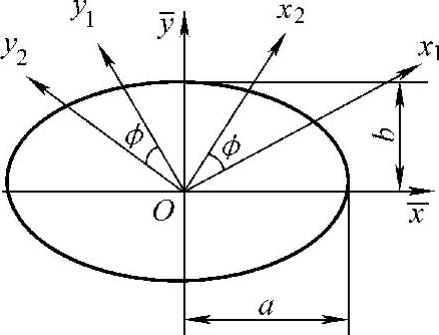
图1.7.3 坐标关系及接触椭圆

（2）接触应力 两曲面接触并压紧，压力P沿z轴作用，在初始接触点的附近，材料发生局部的变形，靠接触点形成一个小的椭圆形平面，椭圆的长半轴a在x轴上，短半轴b在y轴上。椭圆形接触面上各点的单位压力大小与材料的变形量有关，z轴上的变形量大，沿z轴将产生最大单位压力P₀。其余各点的单位压力P是按椭圆球规律分布的。

其方程为

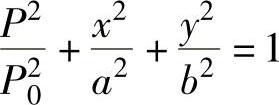
单位压力(www.xing528.com)

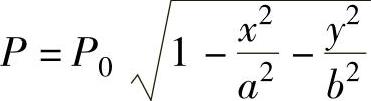
总压力 P_总=∫PdF

∫dF从几何意义上讲等于半椭球的体积，故

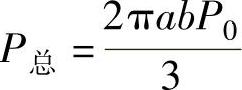
接触面上的最大单位压力P₀称为接触应力σ_H，故

a、b的大小与两接触面的材料和几何形状有关。