(1)机构学上的理想机械与实际机械的不同 机构学上的理想设计与现实中达成的机械有巨大差异,在设计中必须留意这个巨大差异:
1)材料并不是刚体,它随着温度的变化,动与静的负载力影响等会发生变形。
2)现实中的机械构造所组成的元件并不是几何学意义上的理想尺寸和形状,它们具有客观上的尺寸误差、几何偏差及表面粗糙度误差。
3)机械元件在组合装配时,在形成机构约束时,存在着机械干涉和间隙,存在着弹性变形与热变形、电磁变形、重力变形等。
4)在各个约束点与接触部位存在摩擦力,有摩擦损耗,需要润滑,需要对摩擦界面进行优化设计域补偿。
因此,对从力学和热力学意义上并非纯粹几何学意义上的刚体的机械零件来说,如何把它们有序地经过排列组合优化而装配成能够实现高精度和高速度的运动机构,其设计方法必须考究。
(2)运动学的设计和准运动学的设计如图1.6.9a所示,空间内刚体的运动自由度由点接触来进行约束的方法,称为运动学的约束(kinematic constraint)。因为每一个点的接触就可以约束一个自由度,而如果是用5个接触点来约束一个机构的一个自由度,如图1.6.9a所示,这样的机构叫作并进一自由度机构,即直线运动机构。把这样运动的物体的约束简化成最少数量的点接触的设计,称之为运动学的设计(kinematic design)。而相反地,把接触点增加,或者如图1.6.9b所示那样把点接触变成了线接触甚至面接触,物体运动的约束设计成为过剩约束的设计,这种设计可称之为准运动学的设计(pseudo-kinematic design)。运动学的设计从制造上来说比较简单,但是由于点接触的约束之下伴随有局部的弹性变形,只能用在刚度条件要求不高的装置上;而准运动学的设计不管是线接触还是面接触,都远较点接触的刚度高,特别是那种四个面都约束在双V形导轨之中的机构,刚度很高,但是制造的难度特别大。
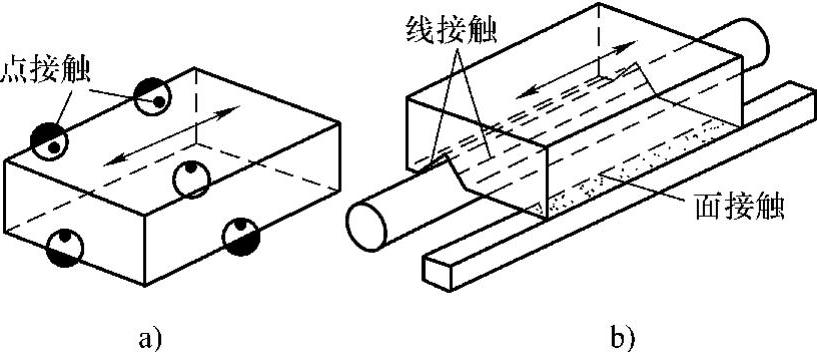
图1.6.9 平行移动一自由度机构的例子(https://www.xing528.com)
a)运动学的设计 b)准运动学的设计
(3)三点支持 作为采用最少数量的点接触来规范约束物体的运动设计实例之一,是机械安装面的三点支持构造。众所周知,几何学上三点可以决定一个平面的位置,机械安装的基准面用三点来支持是最简单而易行的方法。并且,这种构造如图1.6.10a所示,用整个基准面来支持机械的自重显然容易受到变形的影响,而如图1.6.10b所示用三点来支持机械构造体时,可以隔离地基基准面的变形影响,这个方法也常用在机械构造体之间的对接处。
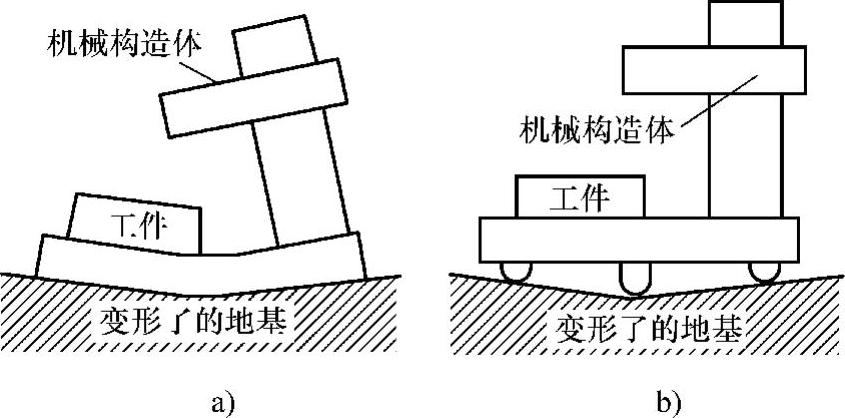
图1.6.10 用三个点支持隔断地基变形
a)机械地基易受变形 b)不易受到地基的影响
(4)误差平均化效果(averageing effect) 按图1.6.9a那样用点接触的方法来约束物体的运动,其结果如图1.6.11a所示,一个轮子(比喻一个接触点的约束)的运动轨迹就完全取决于导轨的凹凸不平了;而如图1.6.11b所示,增加接触点的数量,或者从点延伸为线接触甚至面接触,那么在过剩的接触点的约束处由于弹性变形的发生,不仅提高了接触刚度,而且提高了运动精度,这就是误差平均化效果的原理。这个原理应用在滚动导轨和滚珠丝杠上,通过对导轨或丝杠进行预压紧处理,使之刚度增大的同时,运动精度也得到提高。
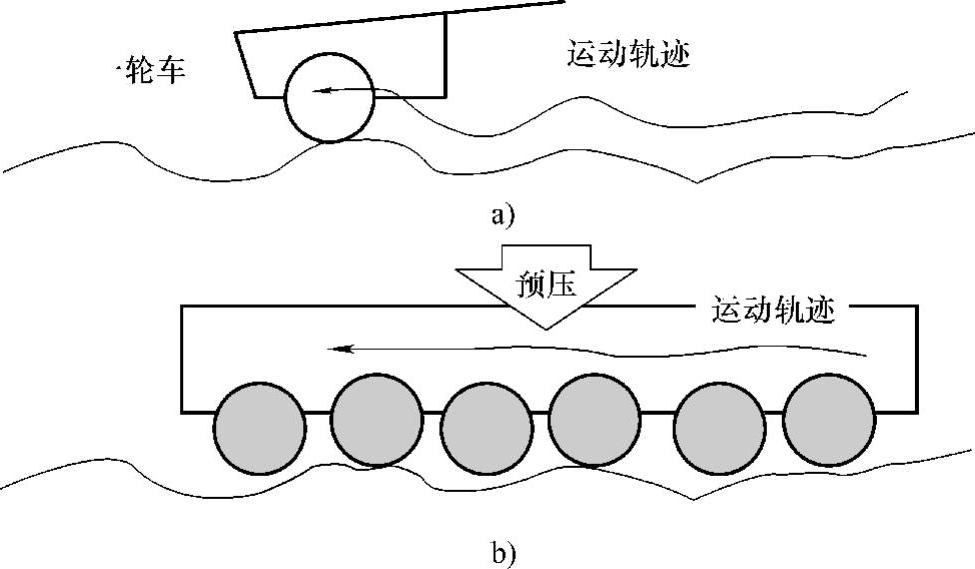
图1.6.11 运动误差的平均化效果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




