感应电动机矢量变换控制优化

1971年德国学者F.Blaschke提出了感应电动机磁场定向型矢量变换控制理论，实现了能找出两个分别决定磁通和电磁转矩的独立控制量，并且求出了这两个控制量与直接测量及控制的定子坐标变量之间的关系式，使得感应电动机的电磁转矩能像直流电动机一样解耦独立控制。因此在感应电动机的动态分析和控制中，坐标系统的选择是关键，采用合适的坐标系统能使问题简化，控制简单，并准确获得良好的动态性能^[3]。

感应电动机矢量变换控制就是将用静止坐标系所表示的电动机矢量变换到磁场定向的坐标轴系，这里包括转子磁场、定子磁场、气隙磁场。三相电流（可以是转子电流或定子电流）经过由三相静止坐标系到两相垂直静止坐标系，再由两相垂直静止坐标系到两相旋转坐标系的变换，并使m轴沿着磁链的方向，则感应电动机就变成了由励磁电流分量i_m和转矩电流分量i_t分开控制的直流电动机。按照直流电动机的控制方法，求得控制量后，再经过坐标反变换，就能控制感应电动机，对感应电动机的控制转为对磁链参照系下的直流电动机的控制。

矢量变换是一组矩阵表达式。矢量变换包括三相静止坐标系到两相静止坐标系的变换（称Clarke变换或3/2变换），两相静止坐标系到两相旋转坐标系的变换（称Park变换），以及直角坐标到极坐标的变换（称K/P变换）。

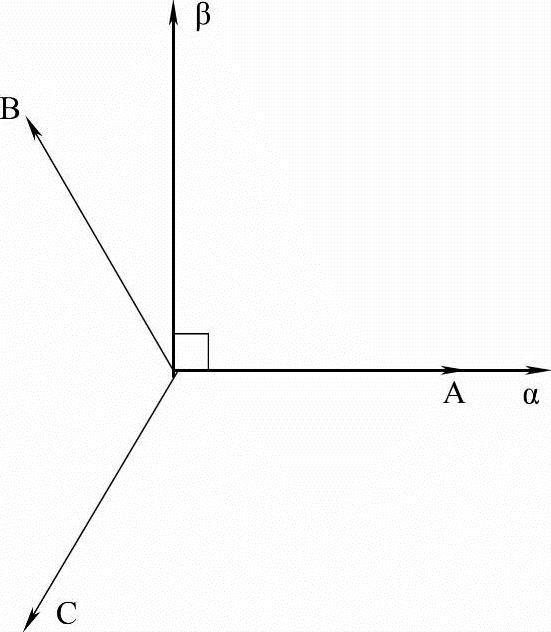
图8-3 三相静止坐标系到两相静止坐标系的变换

图8-3所示为三相静止坐标到两相静止坐标的变换，图中的三相坐标系A-B-C变换到两相坐标系α-β。

从矢量合成的角度推导，一个矢量从一个三相坐标系A-B-C变换到两相坐标系α-β也称为3/2变换，反之为2/3变换。

现以电流矢量的变换来简单说明其变换关系式，矢量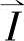在三相坐标系下可表示为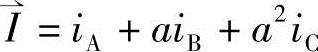，在α，β两相坐标轴系下可表示为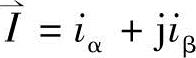。根据坐标变换保持矢量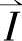不变的原理，在矢量图中，可以得到沿α轴分解的分量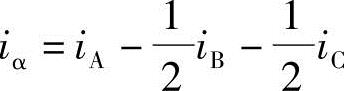，以及沿β轴分解的分量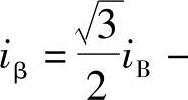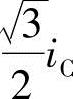。写成矩阵形式为

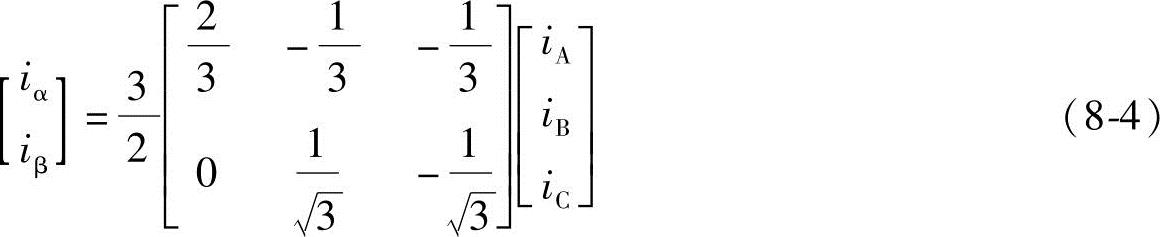
则3/2变换矩阵C_3/2为

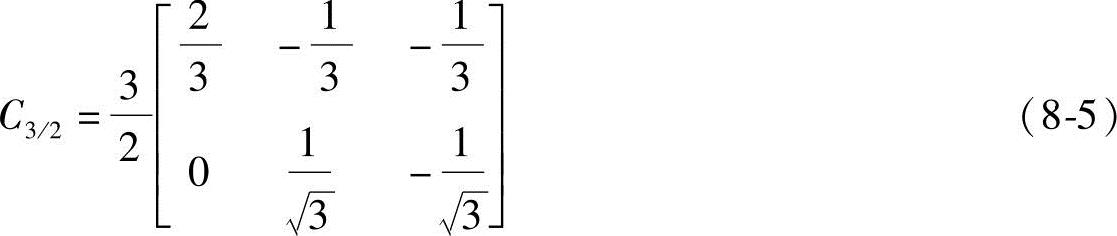
如果三相平衡，即i_A+i_B+i_C=0，则可以推出

则简化后的矩阵形式为

由式（8-7）可以看出，i_α的幅值是i_A幅值的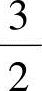倍，这是保证变换前后合成矢量幅值不变的前提，即三相和两相产生的合成电流矢量相同。同理，可以推导出逆变换为

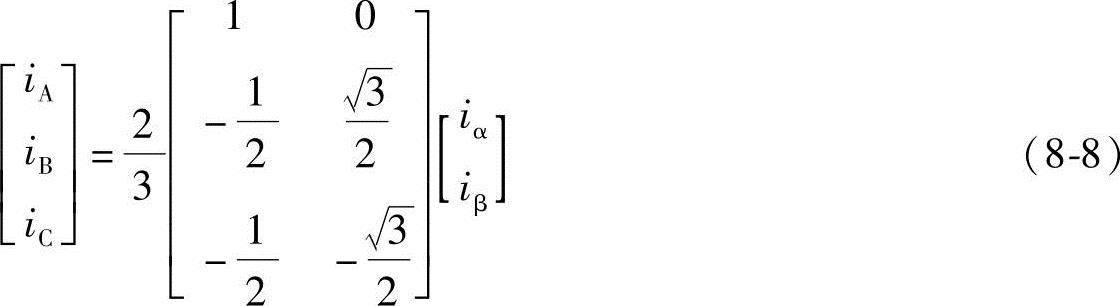
式中，从两相静止α-β坐标系变换到三相静止A-B-C坐标系，2/3变换矩阵C_2/3为

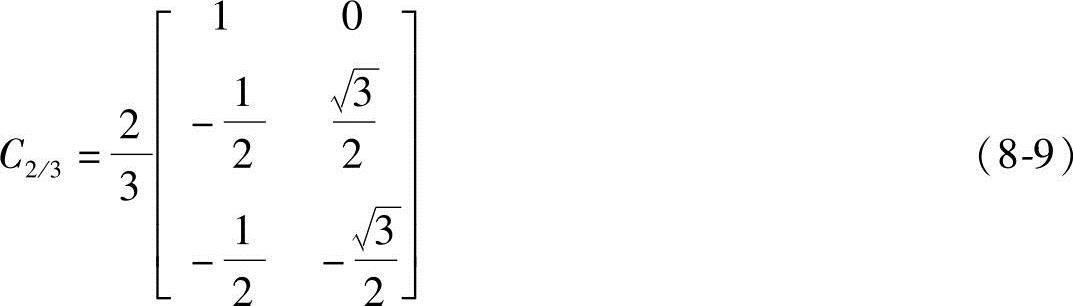
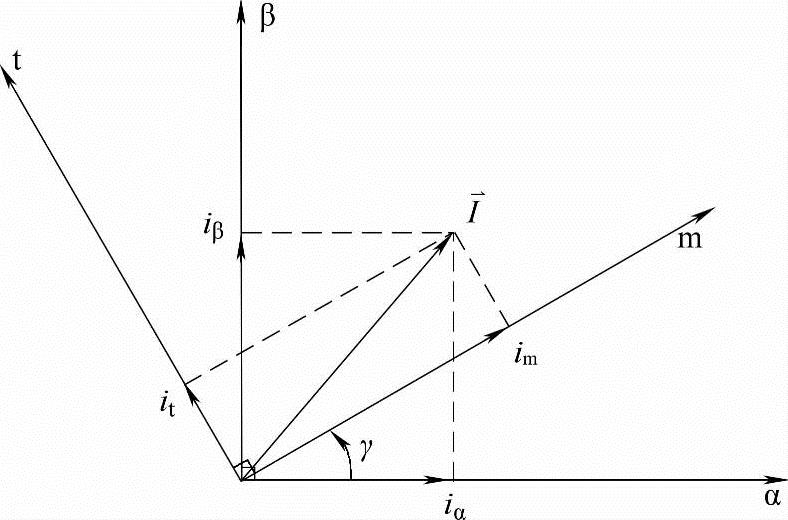
图8-4 m-t轴系与α-β轴系关系图

图8-4所示为两种坐标系，α-β为两相静止坐标系，m-t为两相旋转坐标系。如果让m-t坐标以同步角速度ω_s旋转，则产生的磁动势与α-β坐标系等效。m轴和α轴的夹角γ（亦即m轴和A轴夹角）是一个变量，随负载、转速而变，不同时刻有不同的值。

由此得变换关系式为

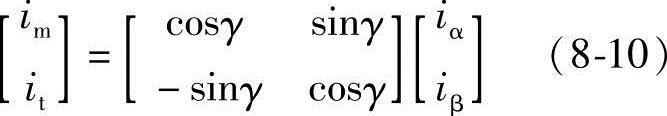
由图8-4可见，从两相静止坐标系α-β到磁链坐标系m-t的夹角即磁链位置角φ_s，α-β坐标系变换到m-t坐标系的变换矩阵为

同理，可以推出反变换矩阵为

如果直接由三相坐标系直接变换到旋转坐标系，则将旋转变换式（8-12）与式（8-5）相乘，得到A-B-C坐标系直接变换到旋转坐标系m-t的变换矩阵

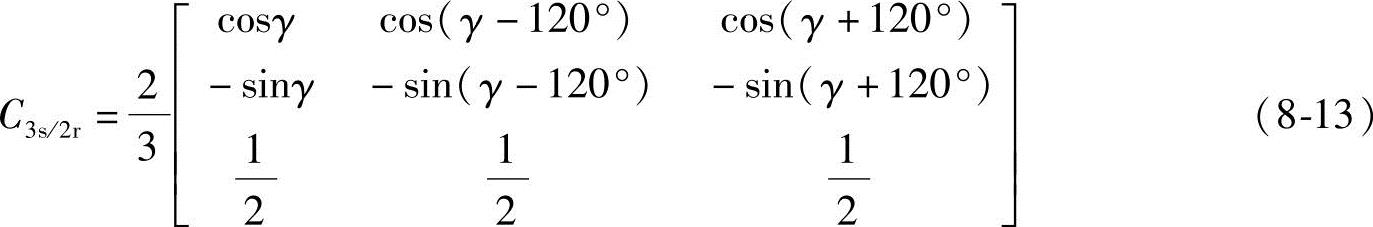
同理求得m-t轴系变换到A-B-C轴系的变换矩阵为

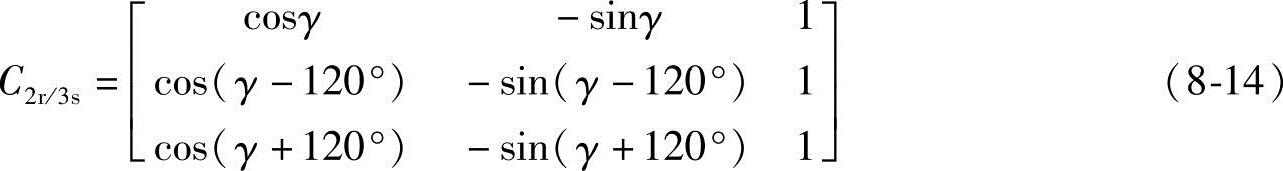
在计算磁动势时，采用极坐标系能简化计算和分析。设合成矢量与m轴的夹角为φ，则直角坐标与极坐标其变换关系式

，由于tanφ幅值变化过大，因此常用公式（8-16）

由于在理论分析和实际运行过程中，双馈交流感应电动机的磁链、电压、电流等物理量都是以其基波形式来进行研究的，并且电动机内部绕组采用了分布、短距、斜槽等措施，其气隙磁场具有很小的谐波，因此将其视为“理想感应电动机”来进行研究和分析，如图8-5所示。“理想绕线式感应电动机”的假定如下^[4]：

1）忽略铁磁饱和、磁滞及涡流等的影响，不计铁心和导线的集肤效应；(www.xing528.com)

2）转子为圆柱形，气隙均匀，忽略定子、转子齿槽的影响，认为定子、转子都有光滑的表面；

3）忽略温度变化对于电动机有关参数的影响；

4）定、转子三相绕组对称，每相绕组均在气隙中产生正弦形分布的磁通密度。

在三相静止坐标系下，异步电动机的定子三相对称绕组A，B，C在空间是固定的，A相绕组的中轴线是该坐标系的参考坐标轴，转子三相对称绕组a，b，c以转子角速度ω_r逆时针旋转，转子a轴和定子A轴夹角为θ。并规定各绕组电压、电流、磁链的正方向符合电动机惯例和右手螺旋定则。这时感应电动机的数学模型由电压方程、磁链方程、转矩方程和运动方程组成^[5]。

（1）三相坐标系下的电压方程。

三相定子电压平衡方程为

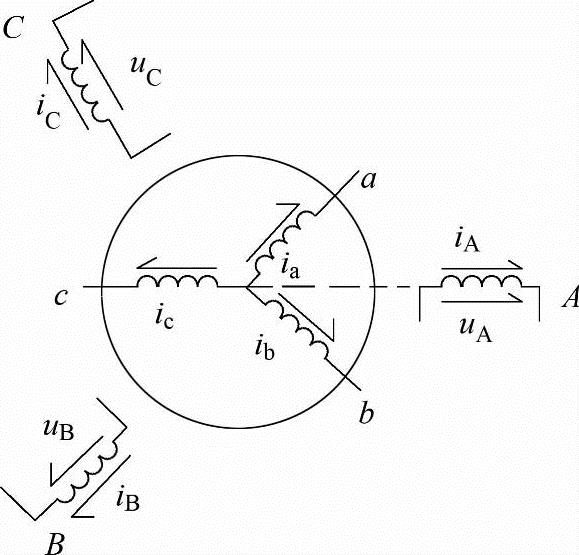
图8-5 绕线式三相感应电动机示意图

相应的三相转子折算到定子侧后的电压方程为

式中，u_A，u_B，u_C，u_a，u_b，u_c分别为定、转子各相电压；i_A，i_B，i_C，i_a，i_b，i_c分别为定、转子各相电流；设R_s，R_r分别为定、转子相电阻，由于定、转子绕组对称，因此R_A=R_B=R_C=R_s，R_a=R_b=R_c=R_r；ψ_A，ψ_B，ψ_C，ψ_a，ψ_b，ψ_c为各绕组磁链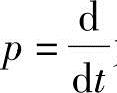；为微分算子。

写成矩阵形式为 [U]=[R][I]+p[ψ]

即

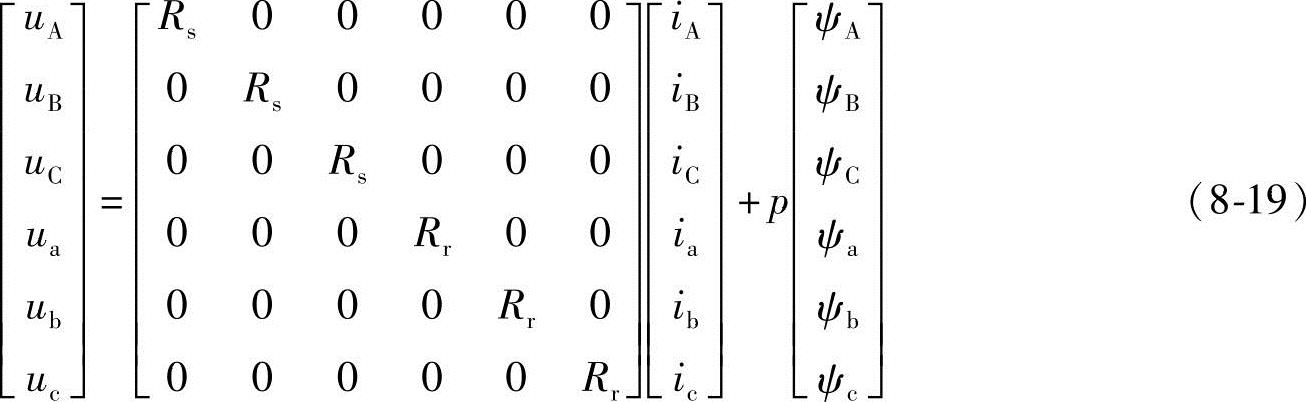
式中，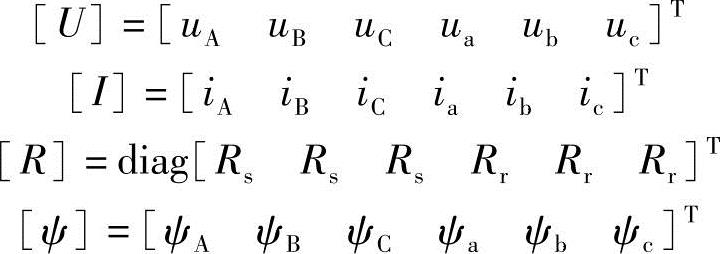

其中对角线元素L_AA，L_BB，L_CC，L_aa，L_bb，L_cc是各有关绕组的自感，其余各项则是绕组间的互感。

（2）磁链方程。

[ψ]=[L][I]

其中每个绕组的磁链是它本身的自感磁链和其他绕组对它的互感磁链之和。

以定子为例，每相绕组的全自感系数包括两部分，一部分是只与该绕阻交链但不穿过气隙的漏感L_sδ，还有一部分是穿过气隙且与其自身绕组相交链的主磁链对应的主电感L_sh，因此定子每相全电感

L_AA=L_BB=L_CC=L_sh+L_sδ

同理，转子每相全电感

L_aa=L_bb=L_cc=L_rh+L_rδ

两相绕组之间只有互感。定子和转子的三相彼此之间位置都是固定的，它们的轴线在空间的相位差是±120°，假定气隙磁通为正弦分布的条件下，互感值为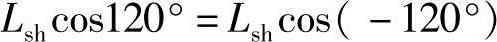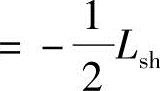，于是

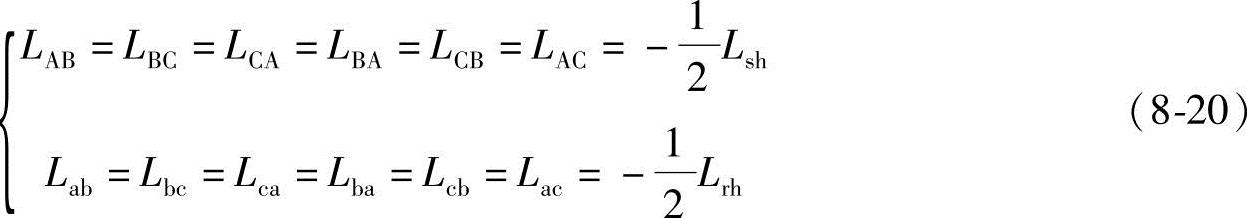
由于定子任一相与转子任一相之间的位置是变化的，因此互感是转子位置角θ的函数

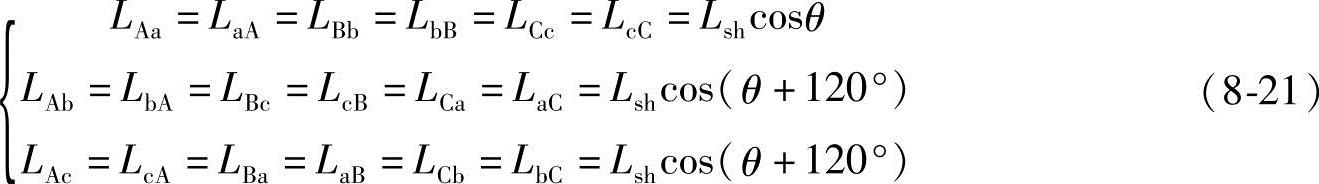
式中，s代表定子侧，r代表转子侧；θ为转子轴和定子轴夹角。

（3）运动方程。

电动机的机械运动方程为

式中，T_e为电动机额定输出转矩；T_L为负载转矩；J为电动机转轴上总的转动惯量；n_p为电动机极对数。

（4）电磁转矩方程。

根据机电能量转换的理论可知，极对数为n_p的感应电动机电磁转矩T_e处理后的表达式^[6]为

T_e=n_pL_h[（i_Ai_a+i_Bi_b+i_Ci_c）sinθ+（i_Ai_b+i_Bi_c+i_Ci_a）sin（θ+120°）+（i_Ai_c+i_Bi_a+i_Ci_b）sin（θ-120°）] （8-23）