感应电动机空间矢量控制技术

任何在空间按正弦形式分布的物理量都可以用空间矢量表示。下面以感应电动机定子绕组为例，感应电动机的定子绕组均采用对称的三相绕组，当三相交流电流i_A，i_B，i_C流入三相绕组后，就形成旋转的绕组磁势。若略去空间谐波磁势，则各相绕组产生的基波磁势可分别用每相磁势空间矢量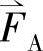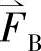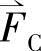，，表示，其长度代表基波磁势的大小，分别与各相电流的瞬时值成正比，其方向代表基波磁势幅值所在的方向，分别处于各相绕组的轴线上^[1]。基波磁势空间矢量如图8-1所示。

在图8-1中，若取轴线A作为实轴Re，虚轴Im领前于实轴Re，则在此电动机剖面的空间复平面内，有下列关系式成立：

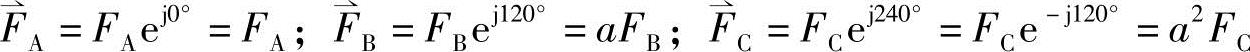
式中，F_A，F_B，F_C分别表示各相基波磁势的幅值。

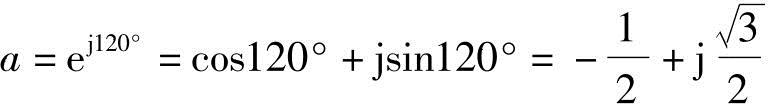
根据矢量合成法则，将各相磁势空间矢量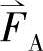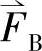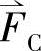，，相加，可得到三相合成磁势空间矢量。取合成磁势的2/3定义为磁势空间综合矢量（简称为定子磁势空间矢量），用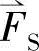表示，则有

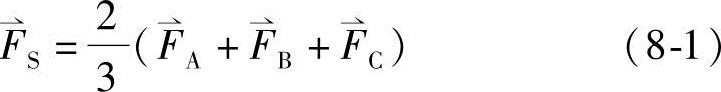
磁势空间矢量可表示为

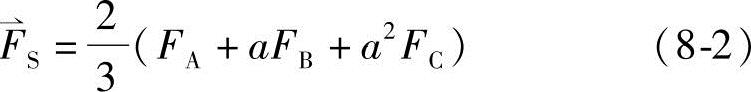
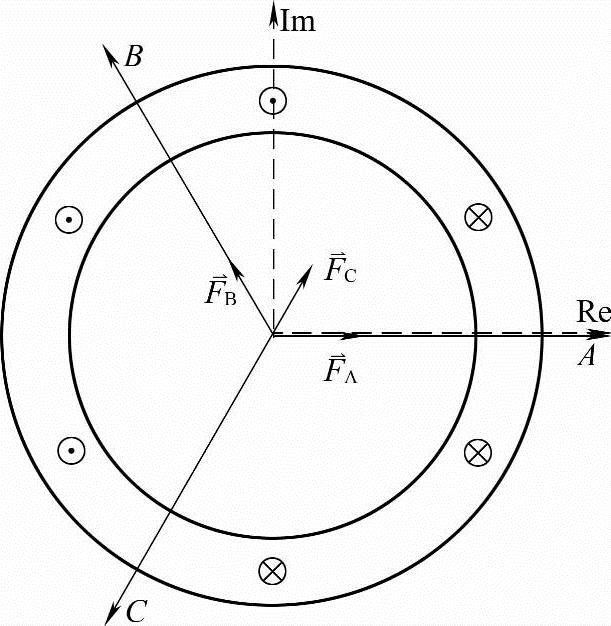
图8-1 基波磁势空间矢量

由于磁势的大小和电流成正比，因此在三相系统中，若各相的相电流瞬时值分别用i_A，i_B，i_C表示，则这三个瞬时值电流构成一个定子电流空间矢量，用I_S表示。(www.xing528.com)

电流空间矢量在复平面上的表示如图8-2所示。一般说来，电流空间矢量的长度和位置都是随时间变化的。

当三相电流没有零序分量（当电动机三相绕组是星形联结而中点不外接时，此条件可以满足），即i_A+i_B+i_C=0时，可以证明，磁势空间矢量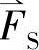在A，B，C三相轴线上的投影正好等于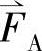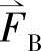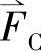，，，且此时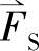和电流i_A，i_B，i_C之间出现了一一对应关系。即任意一组的i_A，i_B，i_C将唯一地确定一个磁势空间矢量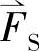，反之亦然。实际上，考虑到三相电流没有零序分量时的约束条件i_A+i_B+i_C=0，一组电流i_A，i_B，i_C只包含两个独立变量，而一个空间矢量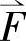也包含着实部的和虚部两个独立变量，所以两者之间有可能一一对应。

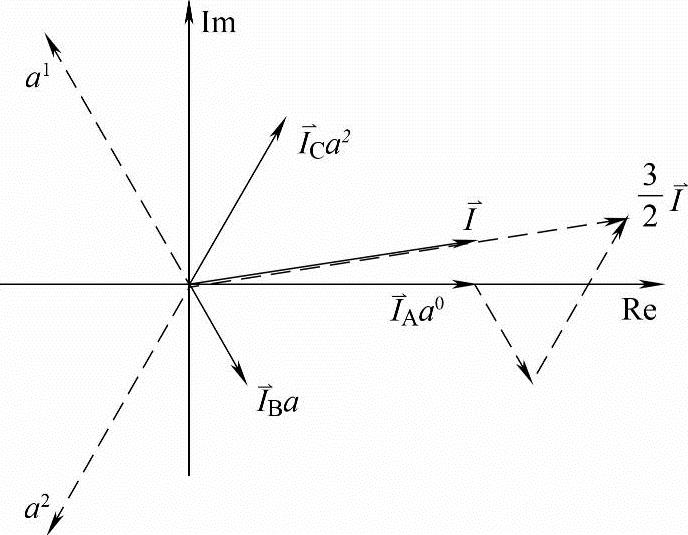
图8-2 电流空间矢量

将三相电动机中各相的物理量综合起来，用空间矢量表达，具有下列优点：

1）电流空间矢量代表三相合成电流，磁链空间矢量代表三相合成磁场，直观且形象化；

2）由某物理量的空间矢量在某一相绕组轴线上的投影，可得到该物理量的瞬时值。所以，根据空间矢量的变化情况，很容易求出各相有关物理量的时间波形图；

3）可以证明，电动机的转矩正比于磁链空间矢量和电流空间矢量的矢积，所以在空间矢量图上能直观地确定电动机转矩的大小和方向；

4）由于引入空间矢量概念时并不要求各相的物理量随时间作正弦变化，因此，变流装置输向电动机绕组的非正弦电流或非正弦电压，也可以用空间矢量加以分析^[2]。