设计模糊控制器：优化方案与实践

模糊控制器输入输出语言变量的选取应该尽量简单，同时又要考虑机器人行驶和避让障碍物的实际情况，较好地反应机器人避障的过程，这里以避障机器人为例，设dr为右侧障碍物距离，dc为前方障碍物距离，dl为左侧障碍物距离；方位传感器测得航向与目标点到机器人连线的夹角为tg。因此模糊控制器的四个输入变量分别是dr，dc，dl和tg；模糊控制器的输出变量有一个，即机器人转向角sa。

模糊语言的确定包括由语法规则生成适当的模糊语言值，根据语义规则确定隶属度函数及模糊变量的论域等。这里使用连续型论域，采用简单线性化处理方法，对每个输入量进行模糊语言描述，如下：

距离输入变量：d={近，远}={near，far}

目标方位输入变量：tg={左大，左中，左小，前，右小，右中，右大}

={lb，lm，ls，zo，rs，rm，rb}

输出转向角变量：sa={左转，左中转，左稍转，直走，右稍转，右中转，右转}；

={tlb，tlm，tls，tz，trs，trm，trb}

模糊分割是指模糊语言对所在论域的划分，决定了模糊控制的精细化程度。模糊分割的越多，控制越精细，但对应控制规则的数目也就越多；若模糊分割太粗，则难以对控制性能进行细致调整。所以，模糊分割的数目并无指导性的方法，主要根据具体情况和经验来划分。例如上面对距离输入变量的划分，通常情况下对距离变量划分为{近，中，远}，但如此一来，模糊规则的数量共有3³×7=189条，较难实现。因此将距离变量简单划分为{近，远}，模糊规则数减少到2³×7=56条。模糊规则数大幅减少，既容易实现，又未过多降低控制精度。

模糊语言值只是一个模糊子集，语言值要通过隶属函数来描述。在论域连续的情况下，隶属度常用函数的形式来进行描述，常见的隶属函数有三角形、梯形、高斯型等。通常，隶属函数的形状越陡，分辨率越高，控制灵敏度也就越高；相反，若隶属函数变化缓慢，则控制特性也平缓，对应的系统稳定性好。因此，在选择隶属度函数时，一般在误差为零的区域附近采用分辨率较高的隶属函数，而在误差较大的区域，可采用分辨率较低的隶属函数，以获得较好的鲁棒性。此外，大多数情况下，隶属函数的选取具有较大的随意性，对同一模糊集不同的人可以选取不同的隶属函数去表述，并无绝对的对错。因此，可以通过改变隶属函数来观察模糊控制器输出的变化。各输入输出变量隶属函数如图7-15、图7-16、图7-17所示。

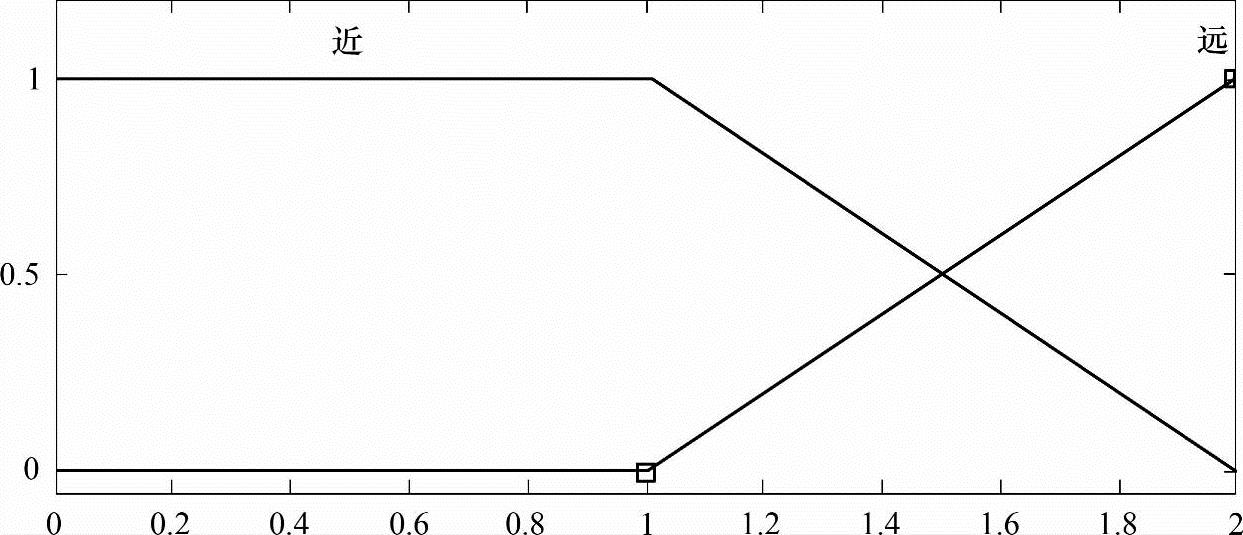
图7-15 dl、dc和dr的隶属函数

模糊规则的建立是模糊控制的核心问题。模糊控制系统是用一系列基于专家知识的语言来描述的，用一系列模糊条件描述的模糊控制规则就构成了模糊控制规则库。根据模糊控制理论，控制规则反映了输入输出变量间的关系。机器人转向的基本原则是：当探测到机器人左/右和前方有障碍物靠近时，机器人应及时转向右/左方。转向角度的大小则视障碍物距离和航向与目标点到机器人连线的夹角而定，障碍物距离越近，转向角越大；夹角越大，转向角越小。根据前面所确定的输入输出集，模糊规则的一般表述形式为“if（条件）then（结果）”。机器人一侧有障碍物是最基本的情况，这里仅以右侧有障碍物的情况来说明。当机器人右侧近距离内有障碍物，而左侧和前方近距离内均无障碍物时。当左右障碍物对称时，根据基本规则，机器人将无法确定行进方向而在两障碍物间来回转向，形成死锁。在这种情况下，目标方位角tg则会决定机器人的转向，这就是局部最优选择。用模糊逻辑表示如下：

如果dc为近，dr为远，dl为远，且目标点在机器人左侧，则机器人左转；if（dr is near）and（dc is near）and（dl is near）and（tg is ls），then（sa is tlb）。(www.xing528.com)

如果dc为近，dl为远，dr为远，且目标点在机器人右侧，则机器人右转。

if（dr is near）and（dc is near）and（dl is near）and（tg is rs），then（sa is trb）。

图7-16 夹角tg的隶属函数

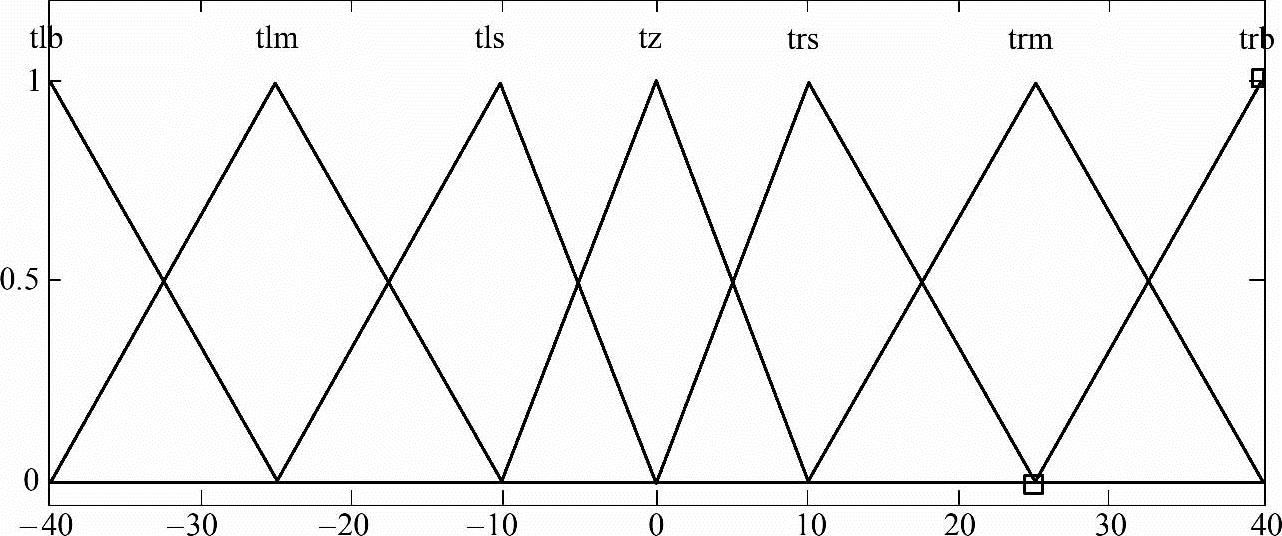
图7-17 输出转向角sa的隶属函数

按照同样的方法，针对不同方位的障碍物和目标方位角，可制定完备的控制规则。这样的规则制定方法是基于控制器行为特征的方式，将动作分为若干的基本行为，对于较复杂的行为，则分由几个较简单的行为依次构成。这样可简化模糊规则的制定，减少模糊规则的条数，避开被控对象特征的建模。模糊控制规则经简化后，放入模糊规则库，供模糊控制器查询。

竞赛智能车多采用两轮驱动，通过对电动机转速与智能车位置的反馈，左、右轮驱动电路主要受PID调节，而对PID控制进行修正则可以使用模糊控制器。智能车运行过程的系统结构图如图7-18所示。

在转向控制算法中，如果仅采用PID控制算法，则为了使机器人行进顺畅，需要在直线运动偏差较小时缓慢调节甚至不调节；在遇到弯道产生大的偏差时，舵机能够迅速动作。这就使得偏差量比例系数P是一个变量，即该参数呈非线性特征，由于P是一个离散的数值，因此将导致转向调节的阶跃式变化，一方面机器人对路径变化反应不灵敏，另一方面也使得控制系统易产生超调及振荡现象。对于追求高车速、短决策周期控制策略的智能机器人来说，通过在PID调节的基础上辅助采用模糊控制算法，可以有效增强系统控制响应速度及对不确定因素的适应性。在寻迹与避障类竞赛中对机器人舵机及电动机控制多采用模糊控制算法。

图7-18 智能车运行过程的系统结构图