微分项优化策略：降低干扰与数据误差

由于微分作用是在相邻的采样周期内进行的，因此它的强弱不仅与微分时间T_D，放大系数K_P有关，而且与采样周期T也有明显关系。当T太小时，两次采样之间被控参数的变化一般也不会太大，因而微分作用较弱。所以通过增加微分时间T_D和放大系数K_P来加强采样周期内的微分作用，这样一来，系统的稳定性及抗干扰能力就会减弱，所以对微分项的改进应该从减少干扰与降低数据误差下手。

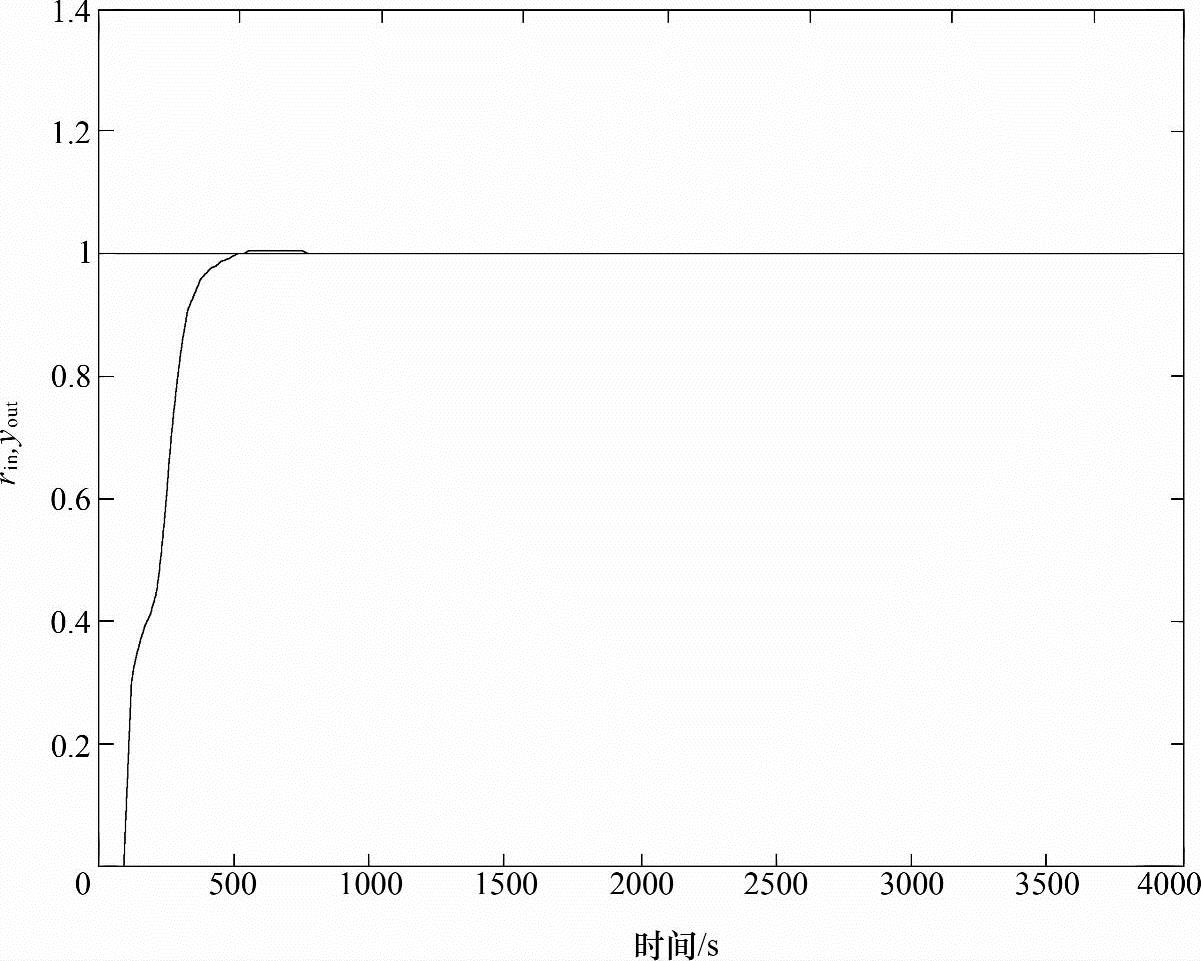
图7-11 采用变速积分控制的阶跃响应曲线

1.偏差平均

偏差平均的公式为

式中，平均项数m取决于被控对象的特性。一般流量信号m取10，压力信号m取5，温度等缓慢变化的信号m取2或1。

2.测量值微分

当控制系统的给定值r（n）发生阶跃变化时，微分动作将导致控制量u（n）的大幅变化，这样不利于生产的稳定操作。因此，在微分项中不考虑给定值r（n），只对测量值y（n）（即被控量）进行微分。考虑到在正反作用下，偏差的计算方法不同，即(www.xing528.com)

e（n）=y（n）-r（n）（正作用） （7-14a）

e（n）=r（n）-y（n）（反作用） （7-14b）

参照式（7-6）中的微分项

Δu_D（n）=K_D[e（n）-2e（n-1）+e（n-2）] （7-15）

改进后的微分项算式为

Δu_D（n）=K_D[y（n）-2y（n-1）+y（n-2）]（正作用） （7-16a）

Δu_D（n）=K_D[r（n）-2r（n-1）+r（n-2）]（反作用） （7-16b）

必须注意，对串级控制的副级控制的副调节器而言，因给定值是主调节器的输出控制量，故上述仅对测量值进行微分的做法并不适用，仍应按原微分项算式（7-15）对偏差进行微分。测量值微分也称微分先行。