分类介绍PID控制算法

1.模拟PID调节器

PID调节器是一种线性调节器，它将给定值r（t）与实际输出值c（t）偏差的比例（P）、积分（I）、微分（D）通过线性组合构成控制量，对被控对象进行控制。PID调节器的微分方程如下：

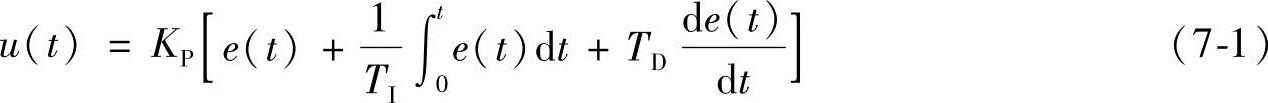
e（t）=r（t）-c（t） （7-2）

PID调节器的传递函数对应如下：

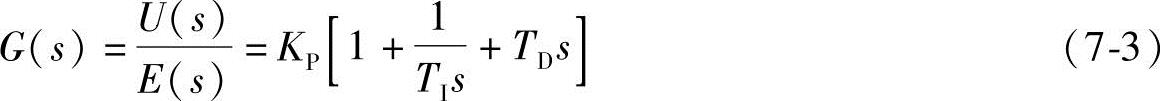
模拟PID控制系统框图如图7-2所示。

图7-2 模拟PID控制系统框图

2.数字PID调节器

为了便于计算机实现PID控制算式，必须把连续函数微分方程改写成为离散的差分方程，模拟PID控制规律的离散化见表7-1。

表7-1 模拟PID算子离散化对照表

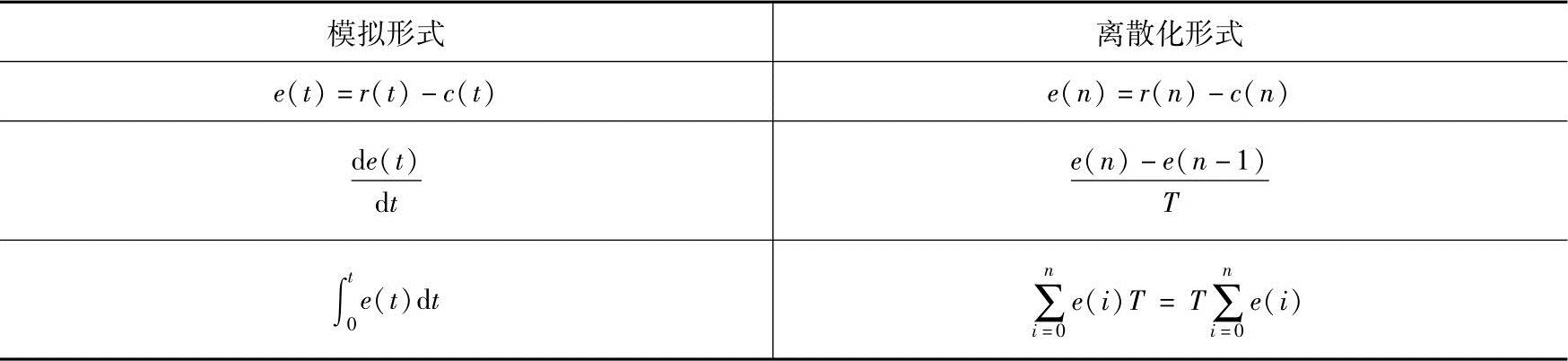
根据式（7-1）结合表7-1可以得出差分方程。

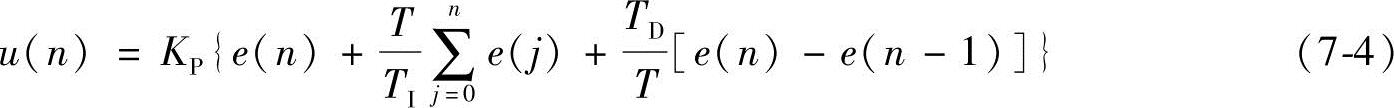
式中，u（n）是第n时刻的系统离散控制量，如果控制周期T比被控对象时间常数K_P小，则该离散控制与连续控制十分接近。由于在模拟PID调节器控制过程中很难实现理想微分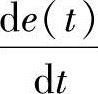，所以通过计算机对差分方程式（7-4）进行近似计算，得到控制参数的方法称为理想微分PID数字控制器。

在计算机控制系统中，数字PID控制算法又分为位置式PID和增量式PID。

（1）位置型PID。模拟PID调节器的调节动作是连续的，任一瞬间的输出控制量u都对应一个被控对象的位置状态，由式（7-4）可知数字PID调节器每一个采样时刻的输出控制量u（n）也与被控对象的位置对应，故称式（7-4）为位置型PID算式（位置式PID）。由于计算机在实现位置型算式的过程中需要不断累加偏差e（j），不仅占用了大量存储单元，而且编程复杂，因此需要对原算式进行改进。

（2）增量型PID。根据式（7-4）不难写出第（n-1）时刻的控制量u（n-1），即

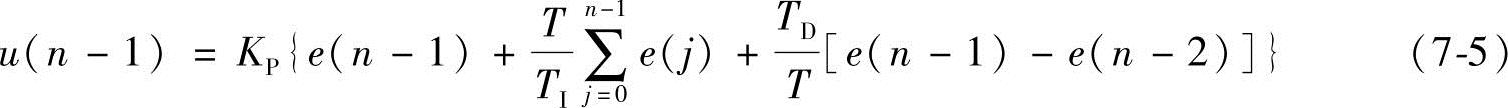
式（7-4）减去式（7-5）后得到n时刻控制量的增量u（n）

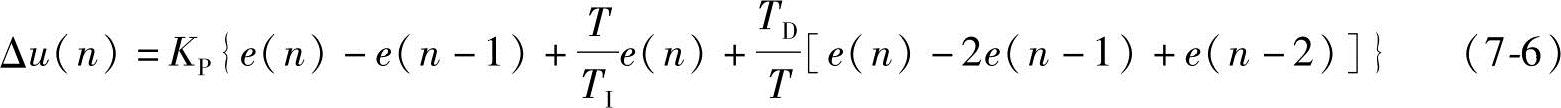
由于式（7-6）中的Δu（n）对应于第n时刻被控对象位置的增量，故称此式为增量算式。因此，n时刻的实际控制量为

u（n）=u（n-1）+Δu（n） (7-7)

式中，u（n-1）为第（n-1）时刻的控制量。(www.xing528.com)

综上所述，计算Δu（n）和u（n）要用到第（n-1），（n-2）时刻的历史数据e（n-1），e（n-2）和u（n-1），这3个历史数据也已在前时刻存于内存储器。通常采用平移法保存这些历史数据。比如，计算完u（n）后，首先将e（n-1）存入e（n-2）单元，然后将e（n）存入e（n-1）单元，以及把u（n）存入u（n-1）单元，如图7-3所示。这样就为下时刻计算机做好准备。

由此可见，采用增量型算式当存在计算误差或精度不足时，对控制量计算的影响很小；另外，增量式易于实现PID调节器手动到自动的无冲击切换。位置型PID与增量型PID控制算法的流程如图7-4所示。

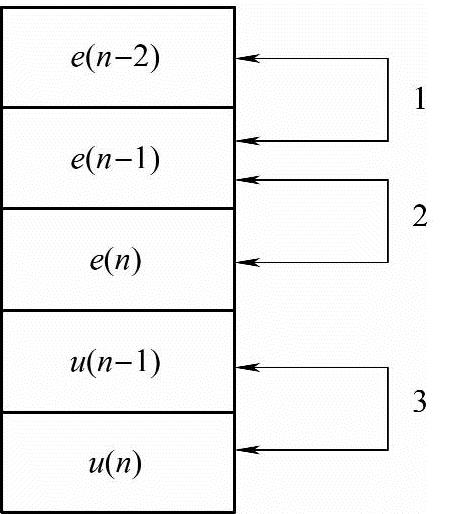
图7-3 增量式保存数据方法

3.不完全微分PID

将微分环节引入智能车的方向和速度控制，能明显改善系统的动态性能，但同时也会使系统对于外界干扰及信号突变特别敏感，影响系统的稳定性。为了克服上述缺点，本文在PID算法中加入了一阶惯性环节。不完全微分PID算法结构如图7-5所示。

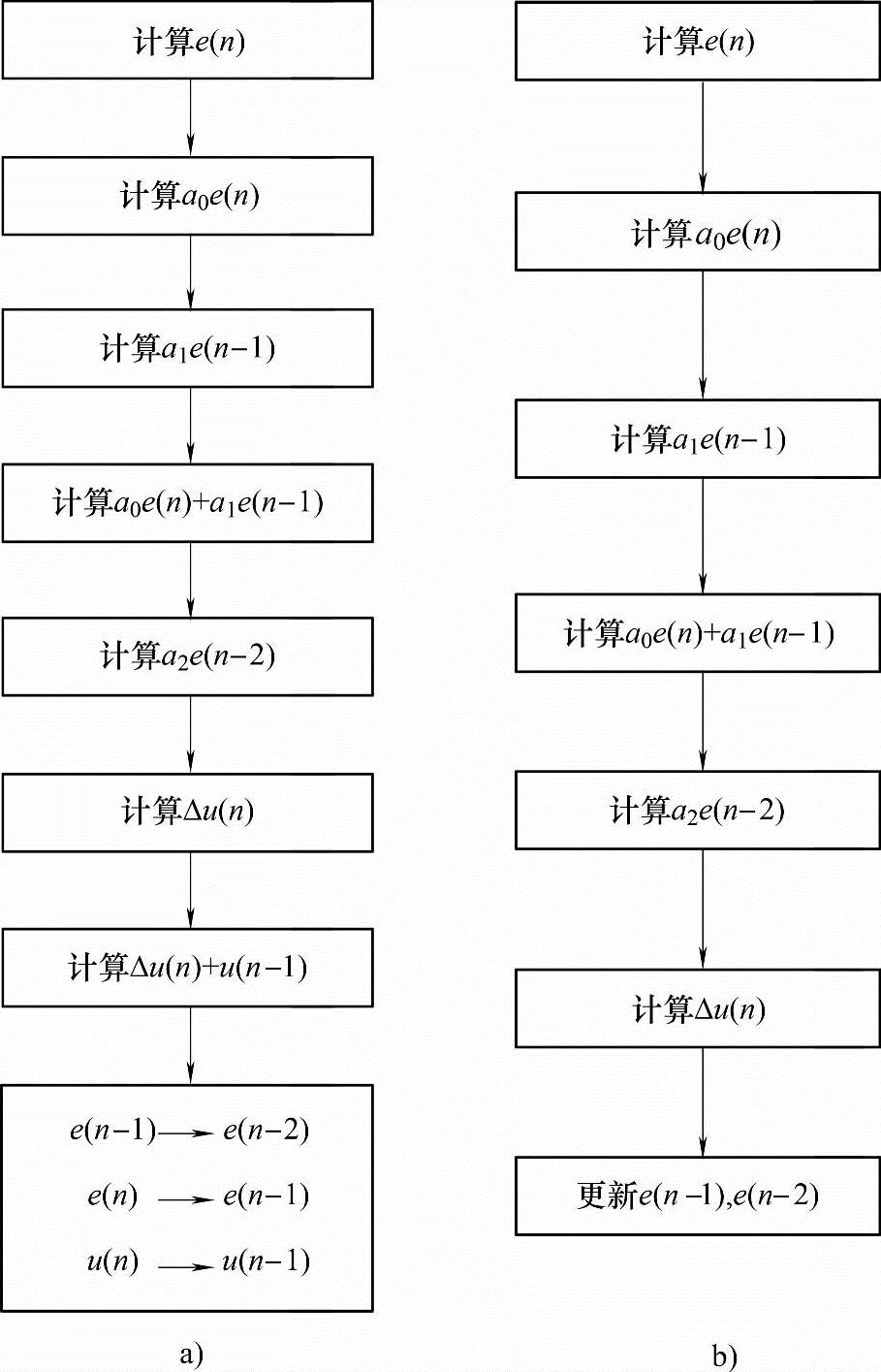
图7-4 位置型PID与增量型PID控制算法的程序流程图

a）位置型PID b）增量型PID

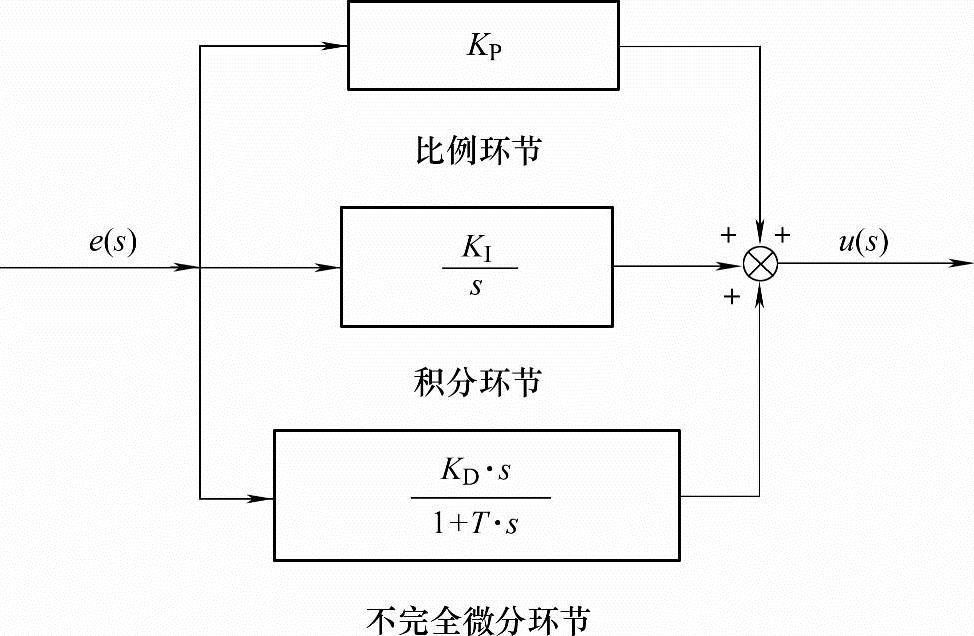
图7-5 不完全微分PID算法结构图

由于普通数字PID调节器的微分作用只在第一个周期内起作用，而不能按照偏差变化的趋势在整个调节过程中起作用，因此第一个周期内的微分作用很强，对于时间常数较大的系统，其调节作用很小，不能达到超前控制误差的目的，容易产生溢出。为了克服上述缺点，通常情况下，为了避免纯微分运算的出现，可以在微分项上加一个一阶惯性环节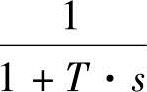，此时可以得到系统的传递函数为

由拉普拉斯变换的微分定理可将频域部分方程转化为时域微分方程并离散化，可求得算式为

u_D（k）=K_D·（1-α）·[e（k）-e（k-1）]+α·u_D（k-1） （7-9）

式中，α为系统时间常数与一阶惯性环节时间常数决定的一个常数。分析式（7-9）可知，引入不完全微分后，微分输出在第一个采样周期有所减小，此后又按照一定比例衰减，由此可见，不完全微分数字PID调节器不但能抑制高频干扰，而且克服了普通数字PID调节器的缺点。不完全微分数字PID调节器输出的微分作用能在各个周期内按照偏差的变化趋势均匀地输出，真正起到了微分的作用，改善了系统的性能。由于在第一个采样周期内不完全微分数字调节器的输出比完全微分数字调节器的输出幅度小得多，有效克服了智能机器人在复杂环境下受到的偏差干扰给速度控制带来的不良影响，因此不完全微分数字PID调节器具有比较理想的调节性能。图7-6所示为不完全微分PID算法的程序流程图。

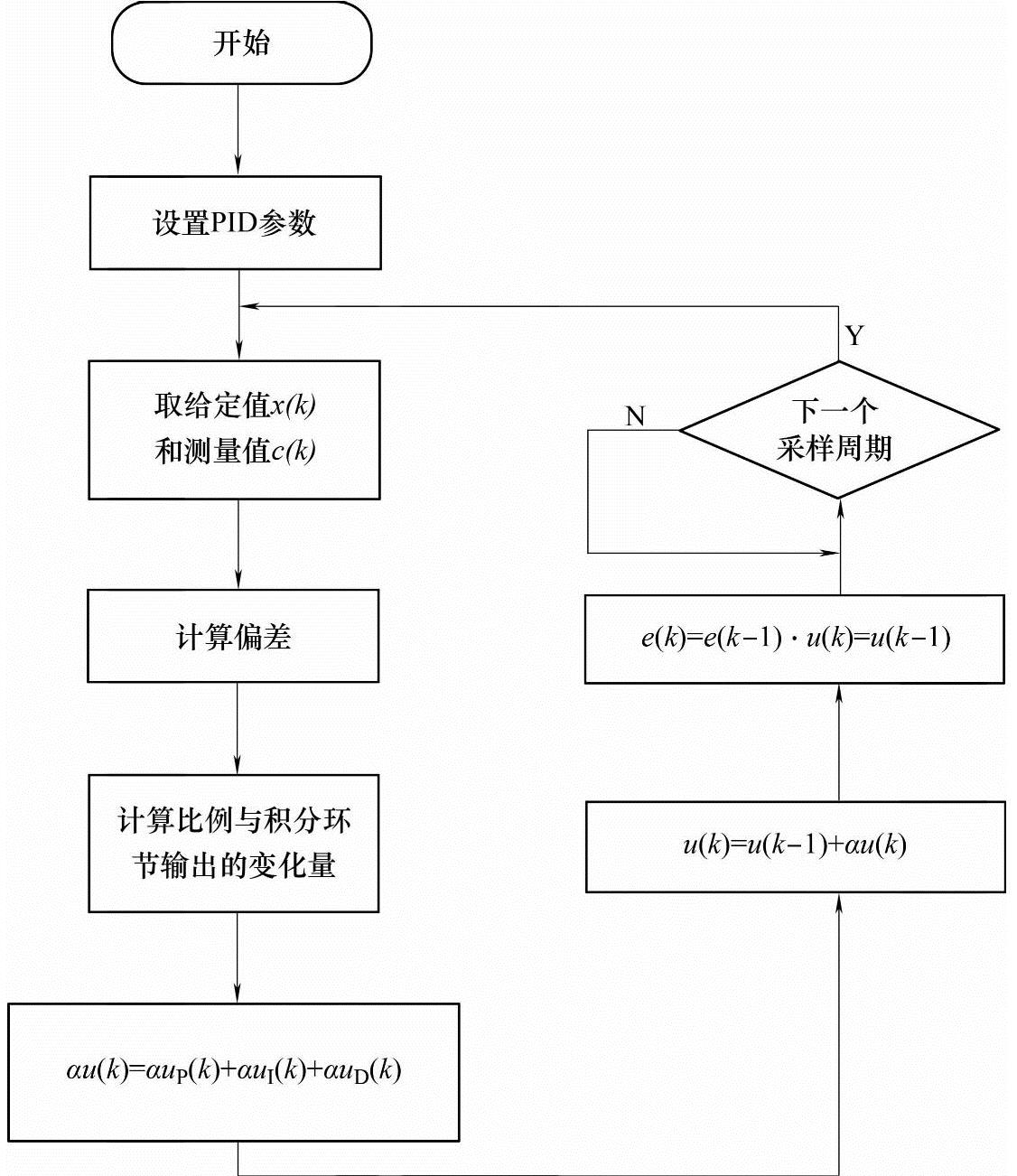
图7-6 不完全微分PID算法的程序流程图

4.微分先行PID

微分先行是把对偏差的微分改为对被控量的微分，这样在给定值变化时输出不会产生大幅度变化。而且由于被控量一般不会突变，因此即使给定值已发生改变，被控量也是缓慢变化的，从而不致引起微分项的突变。微分项的输出增量为

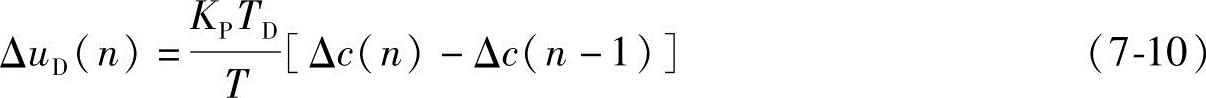
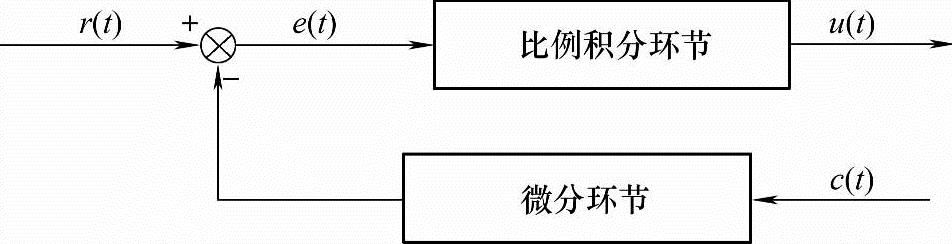
图7-7 微分先行PID控制的结构图

由于竞赛的智能车在场地行驶过程中经常会遇到变速、转弯、爬坡等情况，因此竞赛机器人的速度设定值和方向设定值都会频繁地发生变化，导致控制系统产生振荡影响稳定性。为了消除设定值频繁变化造成的系统振荡，我们在竞赛机器人的速度控制与方向控制上引入了微分先行PID算法，该算法只对输出量（机器人的速度测量值与舵机偏转量）进行微分。这样使得设定值的变化并不会影响到输出量，而被控量的变化相对比较缓和，这就很好地避免了设定值频繁变化给控制系统造成的振荡，有效改善了系统的动态性能。图7-7所示为微分先行PID控制的结构图。