经典流形学习方法探究

在介绍流形学习方法之前，需要强调的是流形学习的几个基本前提和条件，也就是对高维数据的几点要求。①当高维观测空间中两个样本点之间足够近时，它们之间的距离才与低维流形结构上的距离近似相同，称之为局部同胚假设；②高维数据点的数量要足够多，能够密集地覆盖整个流形结构，否则会出现空洞，影响距离计算结果。上述条件保证了观测数据可以近似地表达流形的基本形状，确保了流形学习算法的有效性。

自从2000年以后，流形学习被认为是属于非线性降维的一个分支。然而，由于非线性流形学习算法具有计算量大的缺点，因此，如何将非线性的算法进行线性化转换已经成为流形学习中的一个重要方向。下面将从非线性算法和线性算法两个方面进行介绍。

1.非线性算法

假设从高维空间RH中采集了N个高维向量xi，通过非线性流形学习算法降维到低维的内嵌子空间RL(L＜H)中，得到低维坐标yi。下面介绍几种常用的非线性流形学习算法是如何实现高维向量xi从RH到RL的坐标转换的。

(1)ISOMAP。

该方法是Tenenbaum等人于2000年在著名的Science上提出的，其核心思想是通过距离保持映射，计算高维观测空间中的向量在低维内嵌流形子空间中的坐标值。主要包括三个步骤:构造邻接图、计算测地线距离、内嵌子空间映射。本书在第三章中3.3节对这三个步骤有具体的说明。

ISOMAP算法以观测向量两两之间的距离矩阵为输入，在非线性降维的同时，还保留了经典维数约减算法的主要优点。假设不同类型的多媒体数据集分布在一个内嵌的非线性流形子空间上，可以更好地发现数据集间的非线性结构。Tenenbaum等人已经证实:使用ISOMAP算法来约减维数，不仅能比线性的特征降维方法PCA捕捉到更多有意义的结构性信息，而且当约减到相同维数的情况下，残差也比用PCA的要少。ISOMAP算法在人脸识别、手势识别、图像检索等领域取得了较好的应用成果。

由于ISOMAP算法没有定义高维观测空间到低维嵌入的流形子空间的映射，因此，对于新数据就不能直接投影到流形子空间中。并且，当数据集达不到一定的数量，或者存在过多的噪声时，就难以覆盖真实的流形结构。目前，许多流形学习研究针对这些问题进行了深入的探索。

(2)LLE(Locally Linear Embedding)。

该方法是由Roweis和Saul于2000年在Science上提出的，其基本思想是将高维观测空间中的向量映射到低维嵌入空间的同时，保持局部领域间的相互关系。主要包括下列几个步骤:

步骤1　计算邻域样本:对高维观测空间RH中的每个样本点xi，计算其邻域点Φ(xi)，可以直接采用RH中的欧氏距离，规定与xi的距离小于某一阈值的点为邻域点，或者是以xi为球心，半径在某一阈值范围内的球状邻域。

步骤2　计算重构权值:用邻域点线性重构xi，为xi的每个邻域点Φ(xi)赋予权值wij，并且，使重构误差最小化。重构误差定义为

且重构权值wij满足两个约束条件:当xj不属于xi的邻域时wij＝0；xi邻域内所有点的权值之和为1，即:∑wij＝1。求解权值wij的过程就是求解带约束的最小二乘问题。

步骤3　求解xi在低维空间RL中的坐标yi:LLE算法在求解低维坐标时，最大限度地保留xi在高维观测空间中的邻域，以及线性重构xi所需的权重系数wij。定义低维空间RL的代价误差为

式中，wij的值已知，需要优化L维坐标系下的yi，使得误差最小。对于任何一个样本点xi，wij具有旋转、尺度和全局变换的无关性，因此，对于坐标yi的求解可以转换成一定约束条件下，稀疏矩阵的特征根计算问题。

可见，LLE算法不需要像ISOMAP算法那样计算成对的距离矩阵，并且，流形子空间中样本向量的求解转化成了稀疏矩阵的特征根求解问题，因此，降低了计算量。该算法的特点在于流形子空间的计算过程中，保持了高维空间中近邻样本点间的权重值。然而，对于数据库之外的新数据，就难利用原有的权值来完成流形映射，这也是目前流形学习中的一个共性问题。

(3)Laplacian Eigenmap。

与LLE方法类似，Laplacian Eigenmap也是通过求解矩阵的特征向量，来计算流形子空间坐标。主要包括以下几个步骤:

步骤1　构造邻接图:根据样本点xi和xj之间的欧氏距离d(i，j)，如果样本点xj位于以xi为圆心以常参数r为半径的圆周范围内，则在xi和xj之间建立一条边，其权重值为d(i，j)。(www.xing528.com)

步骤2　基于图谱理论，构造流形嵌入子空间的误差方程为

式中，wij＝exp(-d(i，j)2/t)，t∈R

步骤3　定义约束条件yT Uy＝1，其中U为对角阵，且Uii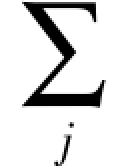＝wij，以及防止流形结构中数据集收缩到某一点的约束:yTUI＝0

步骤4　在上述两个约束条件下，求解Lp＝λUp的最小特征向量，其中L＝U-W。是一个Laplacian矩阵，即:对称的半正定矩阵。已有文献证明，最小化误差方程可以对应于求得的若干个最小特征向量，以此作为流形的最优嵌入。

2.线性算法

非线性的流形学习方法在计算流形嵌入空间的时候，大多是以训练集中所有样本点的邻域关系为基础，而对于训练集之外的新数据，很难实现流形子空间中的坐标定位，难以实现增量学习。并且，非线性方法的计算量较大，这都阻碍了非线性流形学习方法的进一步应用。另外，线性的流形学习方法具有计算量小的特点，并且，训练过程中得到的子空间基向量可以实现新数据的引入和定位。

目前，大多数的线性流形学习方法都是在非线性方法的基础上变形得到的，其主要思想是采用线性映射Y＝AX，以AX代替Y进行矩阵的特征值计算。下面以LPP(Locality Preserving Projection，局部保持映射)方法为例，进行详细分析和介绍。

LPP方法是以Laplacian Eigenmaps方法为基础，进行线性化后得到的，最早是在2003年由Xiaofei He提出的。该方法主要是用输出的线性映射关系，来取代Laplacian Eigenmaps方法中的非线性映射关系，以完成高维观测空间中的特征向量到低维流形子空间的线性变换。LPP方法找到了高维空间中隐藏的流形几何特性，并且在线性的条件下，尽可能地保持了Laplacian Eigenmaps方法中用到的局部几何特性。下面是LPP方法的形式化描述。

假设X＝{x1，…，xi，…，xn}，xi∈RH表示维数为H的高维观测特征向量，A为变换矩阵，通过线性变换Y＝AX，使得观测数据集X从RH映射到低维RL空间，用表示Y＝{y1，…，yi，…，yn}，yi∈RL表示RL空间中的样本点。变换矩阵A的计算过程如下:

步骤1　建立邻接图:对于样本点xi∈X，都作为图中的顶点，然后，以欧氏距离为依据，找到xi的k近邻，在xi和近邻样本点之间建立一条边；

步骤2　计算边的权值:w(i，j)＝exp(-‖xi-xj‖2/σ)，其中σ为实参数；

步骤3　求解Laplacian矩阵的特征向量:类似于Laplacian Eigenmaps方法，可以得到形如Lp＝λUp(其中L＝U-W为Laplacian矩阵)的等式:XLXTa＝λXUXTa，其中U为对角阵，且对角线上的元素值为Uii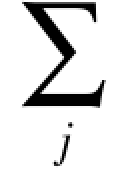＝wji，求解该式的最小特征值，及其对应的特征向量；

步骤4　设步骤三中得到的解为{a1，…，ak}，那么，相应的子空间嵌入映射为:yi＝ATxi，其中，A＝[a1，…，aL]T是L×K维的矩阵。

3.流形学习方法小结

前面介绍的三种非线性流形学习算法都是以局部几何特性为基础的，并假定流形结构是嵌入在高维观测空间中的连续几何结构，将降维过程转换成一定误差条件下的特征根求解问题，不同的是几种方法选用了不同的降维策略。

ISOMAP方法通过计算测地线距离，得到所有样本点数据集的距离矩阵，然后，运用经典的MDS算法挖掘低维的非线性流形结构，因此，这种方法在实现降维的同时，保持了数据集的距离信息，是一种基于局部线性理论的全局几何结构保持映射。LLE方法通过计算样本点邻域，将整个数据空间划分为许多相互交叠的邻域，并在此基础上，用样本点的邻域来重构该样本点。而Laplacian Eigenmap方法则是构造样本点邻域图，并给图中的边赋予适当的权值，于是在图谱理论的基础上，求解一定约束条件下使得嵌入误差最小的流形结构。

总之，各种流形学习方法旨在发现数据集中潜在的内部特性，将其用于高维数据的降维、可视化等各个方面。流形学习方法的核心思想主要是，在降维过程中保持高维观测空间中样本点的局部几何结构，通过线性或者非线性的映射策略计算低维空间中的样本点坐标。近年来，监督式学习、张量学习等概念也被引入到流形学习算法中。