流形学习与流形理论

流形是拓扑学中的概念，最早可追溯到1854年，定义为一个局部范围内处处都是欧几里得的拓扑空间，即:每个点的局部都同胚于d维空间Rd。从数学上来讲，同胚的定义可以描述如下:设X，Y是两个拓扑空间，f:X→Y是一个连续映射，如果f有逆映射，而且逆映射也是连续的，那么f就称为一个同胚映射，且拓扑空间X与Y同胚。

图11-1就是几个同胚拓扑的例子，几个不同大小的凸多面体表面都是同胚的。实际上，几何对象在进行同胚变换时，很多性质都会随之改变，如:角度、距离等，也有一些性质保持不变，而拓扑学正是要研究这些不变性，这一点也为流形学习提供了重要的理论依据。

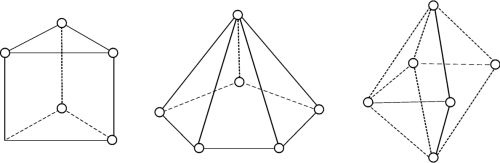
图11-1　几种表面同胚的凸多面体示例(www.xing528.com)

根据上述流形的定义可知，Rd空间本身就是一个流形，各种曲面都是流形，且局部同胚于R2。相对于流形的概念而言，流形学习是一个广泛的概念，它融合了流形和机器学习等多领域的知识，其主要目的是从高维数据集中，寻找出不能直接观测到的结构信息，即找出低维的本征描述，并给出从高维空间到低维流形的映射，找到数据间的内在联系，完成特征提取或者数据挖掘等任务。

2000年，著名的Science上发表了两篇关于如何对高维数据分析的新理论，提出了两种不同的非线性方法:ISOMAP和LLE，揭示了高维空间中隐含的内在低维结构，认为对高维数据的学习可以理解为对内嵌低维流形结构的学习。同年，Science还发表了一篇题为《人脑感知的流形方式》(Manifold Ways of Perception)的文章，在认知层面上进行了深入推测，探索了记忆存储的连续形式和感知流形的关联，暗示着流形学习可能是人类认知中一种自然的行为方式。在随后的几年中，利用流形的特性进行数据降维的研究就成为热门的研究话题，流形学习方法也被应用到各个领域，尤其是会产生高维数据的一些应用中，如:多媒体数据分析、生物特征识别、金融数据分析等等。

如果直接将多媒体数据中提取得到的高维特征向量，输入计算机进行特征分析，将会由于维数过高而失去特征原有的代表性意义，产生“维数灾难”的问题。因此，需要进行维数约减。高维数据的降维是指通过线性或者非线性的映射方法，将高维观测空间中的样本投影到一个低维的子空间中，以找出隐含在高维观测空间中的有意义的低维结构。从一般意义上来讲，数据降维主要有四个目的:去掉噪声、降低存储量、提取识别性高的特征以及实现高维数据的低维可视化。

经典的线性特征降维方法实现简单有效，并且，可以发现线性空间中的真实数据结构，如:PCA和ICA等等。然而，很多情况下，高维数据呈现出非线性的结构。近年来，研究者们提出了很多非线性的降维方法，如:非线性的流形学习方法、神经网络方法、遗传算法等等。