图像颜色信息熵：一种一维颜色特征

颜色特征是图像内容分析与检索中最基础、最可靠、使用最广泛的视觉特征，对图像中物体的大小、方向不敏感，具有较好的稳定性。各种颜色特征计算方法均是基于特定的颜色空间，图像检索研究中主要采用的颜色空间有:RGB(Red，Green，Blue)颜色空间、HSV(Hue，Saturation，Value)颜色空间、LUV颜色空间和LAB颜色空间。

RGB颜色空间是图像处理中最常用的三维空间模型，每个空间维度分别代表像素点的Red，Green，Blue颜色值。现有的图像采集设备最初采集到的图像信息是RGB值，并且，图像显示设备通常也使用RGB值，其他的颜色空间模型都是从RGB空间转换得到。然而，从RGB值中很难知道所代表的颜色属性，不符合人们对颜色的感知心理，两种颜色之间的视觉差异不能采用RGB颜色空间中两点之间的几何距离来度量，这种不直观性正是该空间模式的主要缺点。

HSV空间就是一种符合人眼视觉特性的颜色模型，该空间描述的三种视觉特征是色调(Hue)、饱和度(Saturation)和亮度(Value)。其中，色调反映了光的颜色，光是一种电磁波，其颜色由波长决定，人眼对光谱中间部分的光波最为敏感；饱和度指颜色的深浅程度；亮度则是人眼感受到光的明暗程度。

一般数字图像的显示均是基于RGB颜色空间模型，因此，要实现RGB空间到HSV空间的转换，也就是将图像的R，G，B值转换为H，S，V值的过程，如下式所示:

需要说明的是，在计算H，S，V的值之前，需将上式中的R，G，B值归一化到[0，1]区间。

1.颜色直方图

颜色直方图(Color Histogram)在许多图像检索系统中被广泛采用，反映了图像的一种全局性特征，也就是说不是将图像分成若干个子区域单独处理，而是统一地考虑图像的所有区域。颜色直方图计算了不同的颜色在整幅图像中所占的比例，而不关心各种颜色所处的空间位置关系，因此，对图像中物体的大小、方向不敏感。例如:图3-1(b)中灰度图像的颜色直方图如图3-3所示。

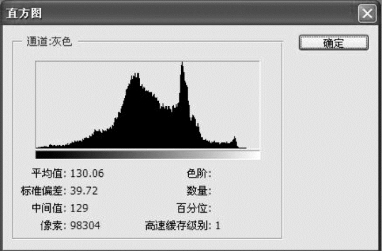
图3-3　颜色直方图示例

例如:一幅640×480像素的24位RGB格式彩色图像，R，G，B值分别用一个字节来存储，设该图像对象命名为sample，则颜色直方图的计算可以采用图3-4中的伪码表示:

图3-4　计算颜色直方图的伪码

在这个例子中，共有2563种可能的R，G，B颜色组合，图3-4中的算法计算了整幅图像中各种颜色值所对应的像素个数，共计640×480＝307200个像素。进一步地，为了使颜色直方图与图像的大小无关，可以将颜色直方图归一化，使得其和为1，就可以有效地消除图像的大小信息。例如:图3-4的算法中640×480分辨率的图像对应的颜色直方图中总像素为307200，而一幅320×240的图像对应颜色直方图的像素总和为76800，通过除以图像中所有像素的总和，进行归一化，就可以消除这种区别。

除了上述方法之外，还可以将颜色空间划分为若干个小的颜色区间，计算图像在每个颜色区间中的像素个数，这种过程称为颜色量化，每个小的颜色区间也称为颜色直方图的柄(Bin)。其他的颜色量化方法还有向量量化、聚类方法、神经网络，等等。

2.颜色矩(https://www.xing528.com)

图像中任何颜色的分布均可以用它的矩来表示。颜色矩(Color Moment)是一种简单有效的颜色特征表达方法。颜色分布信息通常集中在低阶矩中，因此，图像的颜色特征一般采用一阶矩(Mean)、二阶矩(Variance)、三阶矩(Skewness)表示。其数学表示形式分别为

式中，Pij表示第i个颜色通道中灰度为j的像素的出现概率；N表示灰度级数。颜色矩与其他颜色特征相比非常简洁，但是，对于图像检索而言，以颜色矩为基础的图像检索效率比使用颜色直方图要低，主要是因为低阶矩的分辨率稍弱。为弥补这一不足，在实际的图像检索应用中，可以先采用颜色矩缩小搜索范围，再结合其他颜色特征进行检索，以提高检索效率。

3.颜色聚合向量

上述两种颜色特征都无法表达图像中颜色分布的空间位置信息，为此，提出了称为颜色聚合向量(Color Coherence Vector)的特征计算方法，将颜色直方图中每个颜色柄所统计的像素划分为两个部分:聚合像素和非聚合像素。其中，聚合像素是指在某个颜色柄中，占据的区域面积大于给定阈值的像素点，否则为非聚合像素。

假设αi与βi分别表示颜色直方图中第i个(i∈(1，…，n)的整数)颜色柄中聚合像素和非聚合像素的个数，则颜色聚合向量可以用下式表达:

如果将上式变换为＜(α1+β1)，(α2+β2)，…，(αn+βn)>，则可以还原得到该图像的颜色直方图。这种方法考虑了图像中颜色的空间分部信息，是对颜色直方图方法的优化，因此，在采用相同的相似度计算方法的条件下，以颜色聚合向量为图像表达方式可以得到比直方图更好的检索效率。

4.颜色相关图

假设I表示一幅图像，Ic(i)表示图像I中颜色为c(i)的像素集合，则颜色相关图(Color Correlogram)可用下列公式计算:

可见，颜色相关图考虑了图像中像素点间的颜色关系，与颜色聚合向量类似，颜色相关图也反映了颜色分布的空间位置信息。不同的是，颜色相关图还反映了不同颜色的空间相关性，以及某种特定颜色的像素在整幅图像中所占的比例。

5.其他颜色特征

除了上述几种颜色特征之外，还有其他的特征计算方法，如:颜色熵、颜色集等与颜色直方图相关的特征。其中，颜色熵的概念结合了颜色直方图和信息熵，用图像颜色的信息熵来表示其颜色特征，这种特征是一维的。假设图像的颜色直方图经过归一化后表示为(x1，x2，…，xn)，每个维度上的值hi可以看做不同颜色的像素出现的概率密度函数，那么，结合信息熵理论，图像的信息熵可以用下列公式表示:

颜色集特征也是在颜色直方图的基础上得到的，主要包括下列几个步骤:①将RGB颜色空间转换为视觉均衡的空间模式，如:HSV空间；②将颜色空间量化成若干个柄；③在此基础上，采用自动分割算法将图像划分为若干个区域，且每个区域用量化后颜色空间的某一颜色分量进行索引；④得到整幅图像的二进制颜色索引集。这种方法可以进一步结合二分查找树方法加快检索速度，尤其适合大规模的图像数据集。

颜色特征的提取一直是图像特征分析中的基础性研究和热点话题，除了上述传统的颜色特征提取方法之外，一直有研究者们关注新的特征提取和优化方法。例如:改进CSH(Color Shape Histogram)方法，计算了不同颜色在不同图像区域的统计特征；还有研究者受到地理学中区域人口分布统计方法的启发，对环形颜色直方图进行归一化处理，提取出的特征具有尺度不变性；还可以结合小波分析方法计算图像的颜色特征，等等。