语义相似度的度量方法

在CBIR系统中，两幅图像是否相似的判断依据主要是图像的特征是否相似。例如:用户提交一幅图像作为查询样例，系统则从图像数据库中找出与查询样例在视觉特征上相似的图像，并按照相似度大小排序输出。因此，在上述特征提取、降维和索引算法确定之后，相似度计算模型的选择对检索效率有着很大的影响。

由于视觉特征通常可以表示成向量的形式，因此，常用的相似度计算模型大多是基于向量空间模型，即:将图像特征表示成向量空间中的样本点，通过计算两点间的距离来估算两幅图像之间的相似度。常用的相似度计算方法有距离法、统计学方法，以及一些非几何相似性计算方法。

1.欧几里得距离

欧几里得距离(Euclidean Distance)，又称为欧氏距离，是一种应用非常普遍的基于向量空间的距离计算方法，通常用于各分量之间正交或无关的图像特征的距离计算。设X，Y均为n维的图像特征向量，则X，Y之间的欧氏距离定义如下:

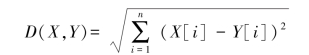
若各个分量的特征不是相同权重时，还需要进行归一化，如下式所示:

2.马氏距离

马氏距离(Mahalanobis Distance)是一种计算复杂权重的欧氏距离，适用于特征向量的各个分量之间具有相关性，或具有不同权重的情况，其数学表达式为

式中，C为特征向量的协方差矩阵，显然，如果C为恒等矩阵，则马氏距离公式则演变为欧氏距离。当特征向量X，Y的各个分量之间没有相关性，则只需要计算各个分量之间的方差ci，此时，马氏距离还可以进一步简化为下式所示:

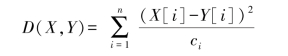
3.直方图的交和二次式距离

直方图的交(Histogram Intersection)和二次式(Quadratic form)距离是计算颜色直方图之间相似度的常用方法。颜色直方图是在许多CBIR系统中被广泛应用的一种颜色特征，描述了不同的颜色在图像像素中所占的比例，不含颜色的空间分布信息。在不同的颜色空间和坐标系下，可以使用不同的颜色直方图。RGB(Red，Green，Blue)颜色空间是一种最常用的颜色空间，大部分的数字图像都是采用这种空间表达。后来，有人提出了HSV(Hue，Saturation，Value)颜色空间、LUV颜色空间和LAB颜色空间，这几种空间表达更加符合人们对颜色的主观认识。(www.xing528.com)

直方图的交是指在两个颜色直方图中，计算每个颜色柄中共有的像素数量。设X*，Y*是两个含有n个颜色柄的颜色直方图，则它们之间的相交距离为

对上式进行标准化操作，除以其中一个颜色直方图中所有像素的总数，将值域范围限制在[0，1]区间内，可以得到

相对于传统的颜色直方图的相交方法，二次式距离在基于颜色直方图的图像检索系统中，显得更为有效，主要是因为这种方法考虑了不同颜色之间存在的相似度。颜色直方图X*，Y*之间的二次式距离计算公式如下:

式中，A＝[aij]为颜色相似度矩阵，元素aij表示颜色直方图中颜色柄i和颜色柄j之间的相似度。通常，矩阵A＝[aij]可以直接从色彩心理学研究中得到。

4.基于流形学习的测地线距离

测地线距离(Geodesic Distance)是在最近几年，对流形学习(Manifold Learning)的研究中提出的一种新型计算模型。2000年，全球瞩目的Science上刊登了关于流形学习的科研论文，掀起了流形学习的热潮。流形学习是一个广泛的概念，自从2000年以后，流形学习被认为是属于非线性降维的一个分支。

假设样本数据均匀采样于一个高维欧氏空间中的内嵌低维流形，流形学习就是从高维的样本点中恢复低维流形结构，即:找到高维欧氏空间中的低维流形，并求出相应的映射模型。可以说，这种方法是从观测到现象中寻找内在本质，找到数据的内在规律。

经过多年的研究和探索，在各个领域中提出了大量的流形学习算法和理论，其中很多方法都是以图模型为基础的，可以称为图嵌入方法。图嵌入方法将数据库中的每个样本看成图结构中的顶点，将彼此为近邻的顶点相互连接，然后采用SDE(Spectral Decomposition Estimation)技术进行嵌入，典型的算法有ISOMAP，Laplacian Eigenmap，LLE等。其中，ISOMAP算法首先构造邻接图；然后，将两点之间最短路径上的权重之和作为测地线距离(Geodesic Distance)，得到距离矩阵；接着采用MDS(Multi-Dimensional Scaling)算法将距离矩阵变为内积矩阵，从而利于谱方法进行嵌入，得到低维的流形子空间。

如图2-3所示，用特征向量表示的图像样本点分布在一个高维的欧氏空间中，任意两个样本点A和B之间的欧氏距离可以用D1表示，而测地线距离D2则是沿着样本所在的流形结构从点A到点B的一条最短路径的长度。

图2-3　测地线距离和欧氏距离示意图