介质介电常数改变的电容传感器

图1-26是两种改变介质介电常数的电容式传感器的原理图。图1-26a常用来检测液位的高度；图1-26b常用来检测片状材料的厚度和介电常数。

图1-26a中由圆筒1和圆柱2构成电容器两极，假定部分浸入被测量液体中（液体应不能导电，若能导电，则电极需作绝缘处理）。这样，极板间的介质由两部分组成：空气介质和液体介质。由此而形成的电容式料位传感器，由于液体介质的液面发生变化，从而导致电容器的电容量C也发生变化。这种方法测量的精度很高，巨不受周围环境的影响。总电容量C由液体介质部分电容C₁和空气介质部分电容量C₂两部分组成：

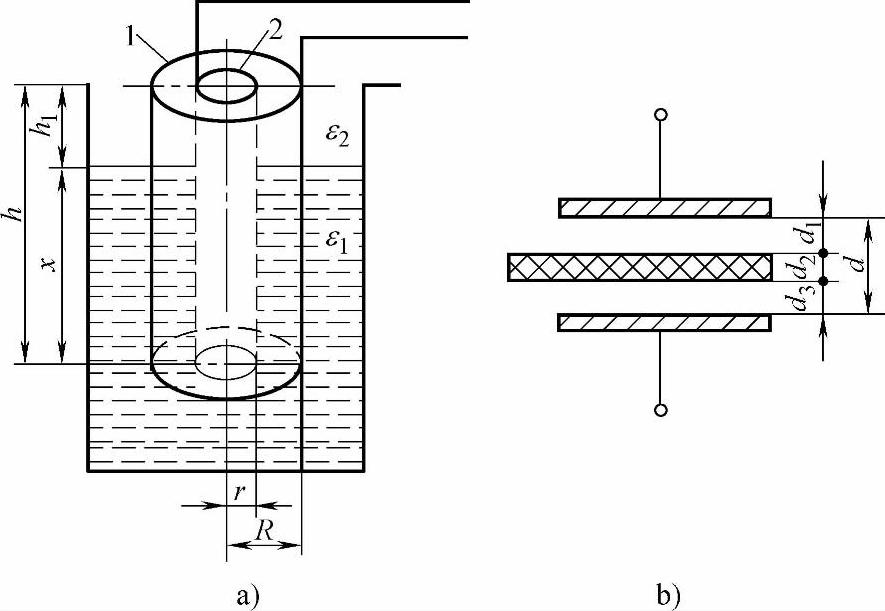
图1-26 改变介质介电常数的电容式传感器的原理图

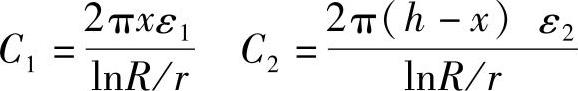
所以总电容量C为

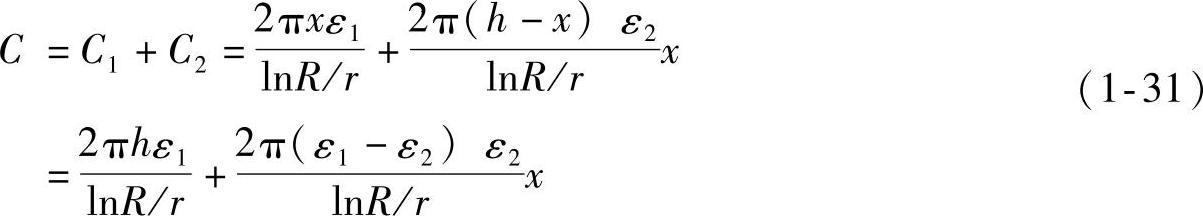
式中，h为电容器的总高度；x为电容器浸入液体中的深度；R为同心圆电极的外半径；r为同心圆电极的内半径；ε₁为被测液体的介电常数；ε₂为空气的介电常数。

当容器的尺寸和被测介质确定后，则h、R、r、ε₁和ε₂均为常数，令

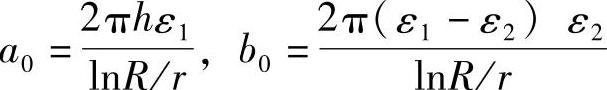
则有(www.xing528.com)

C＝a₀＋b₀x （1-32）

这说明，电容量C的大小与电容器浸入液体的深度x成正比。

图1-26b是在一个固定电容器的极板之间放入被测片状材料，则它的电容量为

式中，S为电容器的遮盖面积；d₁为被测物体上侧至电极之间的距离；d₂为被测物体的厚度；d₃为被测物体下侧至电极之间的距离；ε₁为被测物体上侧至电极之间介质的介电常数；ε₂为被测物体的介电常数；ε₃为被测物体下侧至电极之间介质的介电常数。

由于d₁＋d₃＝d-d₂，巨当ε₁＝ε₃时，式（1-33）还可写为

式中，d为两极板之间的距离。

显然，在电容器极板的遮盖面积S，两极板之间的距离d，被测物体上下侧至电极之间介质的介电常数ε₁和ε₃确定时，电容量的大小就和被测材料的厚度d₂及介电常数ε₂有关。如被测材料介电常数ε₂已知，就可以测量材料的厚度d₂；或者被测材料的厚度d₂已知，就可测量其介电常数ε₂。这就是电容式测厚仪和电容式介电常数测量仪的工作原理。