误差元素检测与建模的介绍

在双主轴车床的几何和热误差元素检测中，使用两种检测仪器：激光测量系统和位移传感器测量系统。使用激光测量系统检测与机床工作台位置有关的误差元素和垂直度误差。使用位移传感器测量系统检测与机床工作台位置无关的误差元素，如主轴热漂移误差和原点热漂移误差。使用温度传感器测量机床各关键点温度。测得数据后，对误差元素进行建模。

1.温度传感器的布置

如图7-25所示，36个电阻温度计（Resistance Temperature Detector，RTD）式温度传感器被安装在机床上检测温度场，图中的传感器号及对应的位置名称见表7-2。

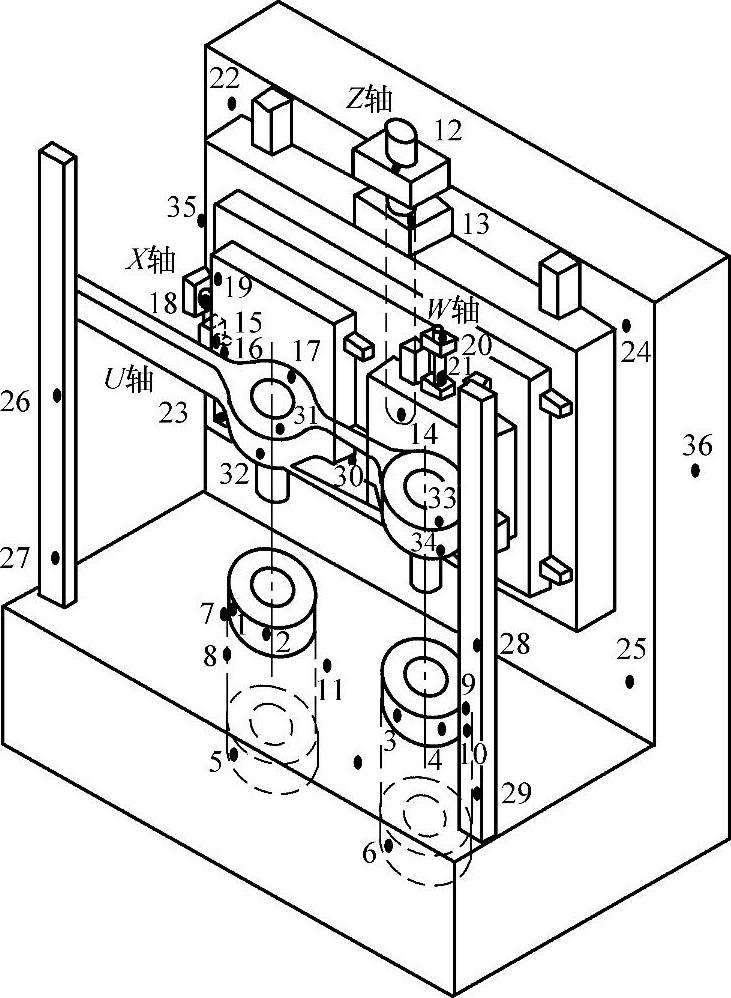
图7-25 温度传感器在机床上的布置

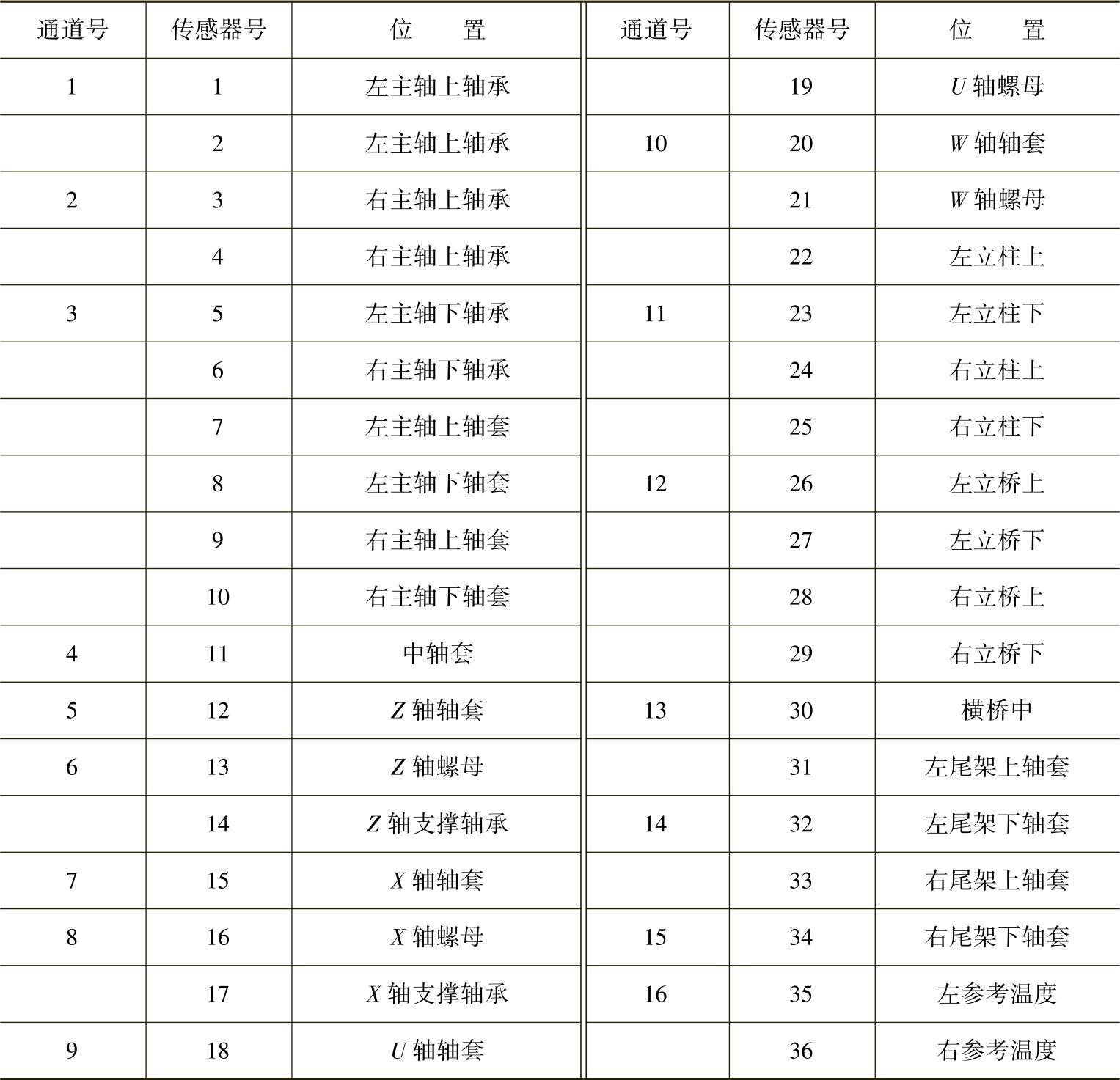
机床关键温度点的选择。首先由主因素策略及模糊聚类，得到了与热误差关系比较大的温度点（见表7-2的传感器号及图7-26中对应的传感器布置位置）：#1、#3、#5、#6、#11、#12、#13、#15、#16、#18、#20、#23、#25、#26、#28、#30、#32、#34、#35和#36，共20个，排除了16个与热误差相关系数比较小的温度点。然后由互不相关策略及模糊聚类，得到#6与#5等类、#25与#23等类、#28与#26等类、#36与#35等类，共4对温度之间相关性强的“同胞兄弟”。在等类温度点中选择一个代表时，考虑到中工作台（X轴工作台）的运动丝杠在机床左边（机床左边温度略敏感于右边）及传感器安装方便（集中布线），故采用“统一从左选”的原则，排除了#6、#25、#28和#36。另外，在关键温度点的选择中，还分析了机床结构及热变形模态。最后仅16个传感器被用于建模而连接到A/D板。表7-2列出了从36个传感器中选出关键的16个连接到A/D板的各通道。最终用于建模的16个温度传感器的布置如图7-26所示（16个温度传感器对应表7-2的16个通道）。

表7-2 A/D板通道与温度传感器连接关系

2.与机床工作台位置坐标有关误差元素的检测和建模

这里讨论主要影响机床加工精度的误差元素。与机床工作台位置坐标有关的误差元素的检测可使用激光测量仪。

（1）X轴误差元素的检测及建模 与机床X轴工作台位置有关的误差元素有线性位移误差δ_xx、直线度误差δ_zx和转角误差e_yx。

1）线性位移（定位）误差δ_xx。在表7-3所列的热循环条件下测量机床线性位移误差δ_xx，持续时间为7h，每20min测量一次。

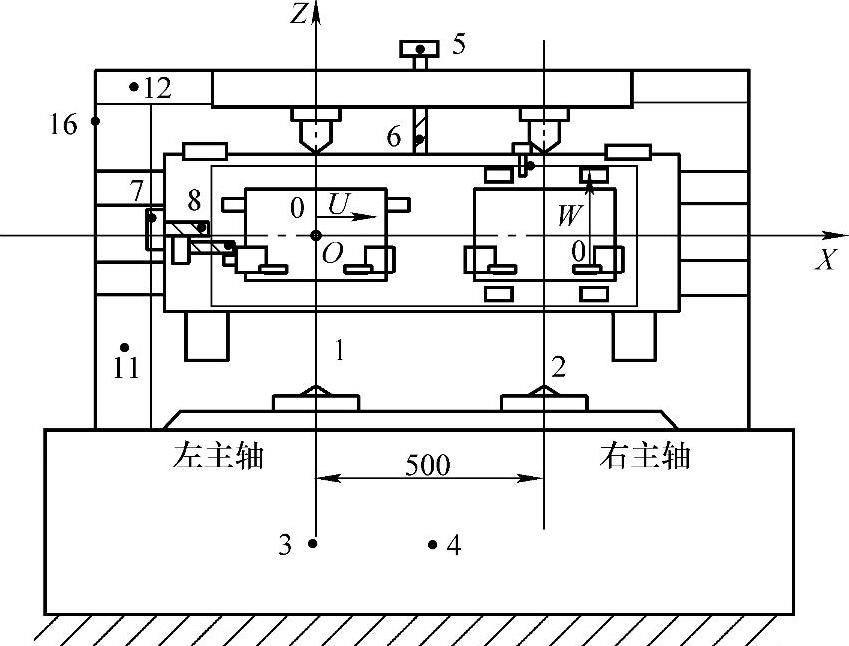
图7-26 用于建模的温度传感器在机床上的位置

注：其他传感器位置参见图7-25。

表7-3 X轴线性位移误差测量中热循环条件

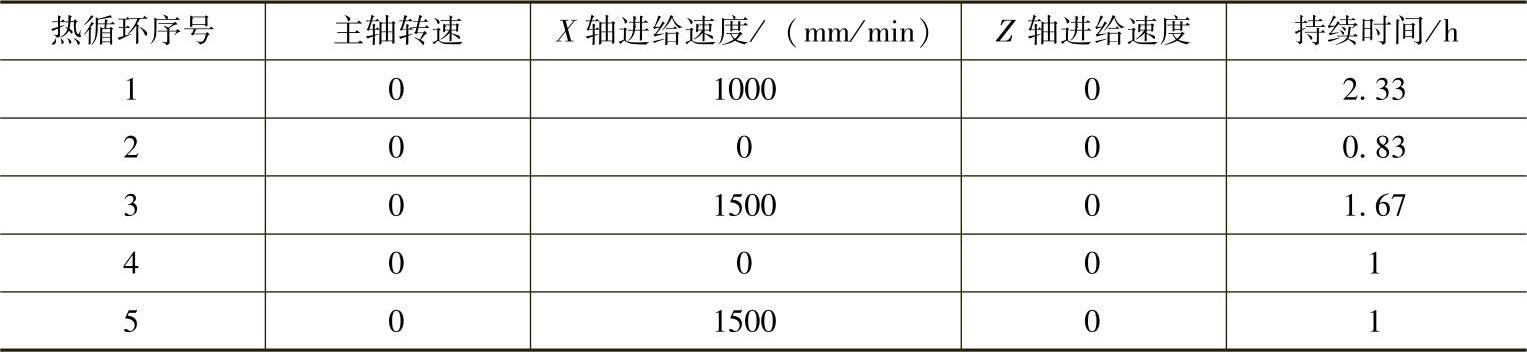
图7-27所示为测量结果（图中仅列出了部分结果）。

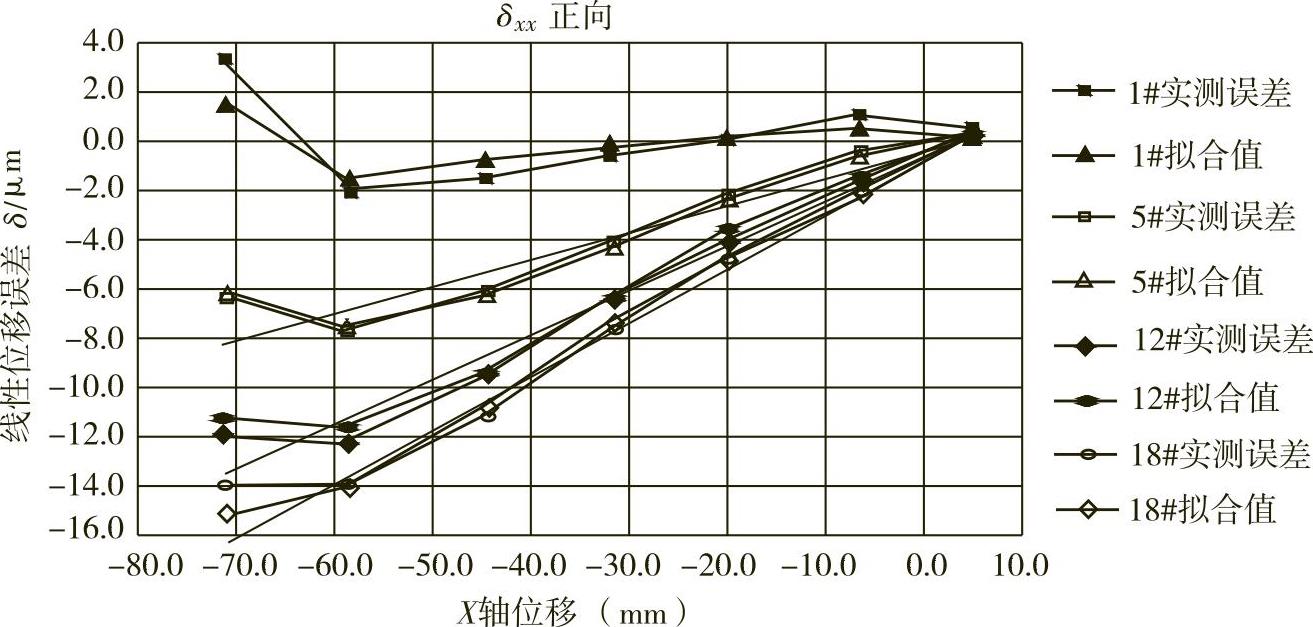
图7-27 X轴线性位移误差δ_xx

从图7-27可知，随着机床受热温度的升高，误差曲线形状变化不大，但曲线斜率有变化。因此，这种误差元素可分离成如下两部分：

δ_xx（x，T）=δ_xxG（x）+δ_xxT（T）·x

式中 δ_xxG（x）——X轴线性位移误差元素的几何部分，它只和位置x有关；

δ_xxT（T）——X轴线性位移误差元素的热部分，它只和温度T有关。

X轴线性位移误差几何部分和热部分的分离如图7-28所示。其中，图7-28a所示为几何部分，在机床冷态时测得。根据误差元素建模理论，用位置x的多项式拟合几何误差δ_xxG（x），可得几何误差模型：

δ_xxG（x）=1.1192×10^-6x⁴+8.9455×10^-5x³+9.0575×

10^-4x²_-6.2218×10^-3x+2.9717×10^-1

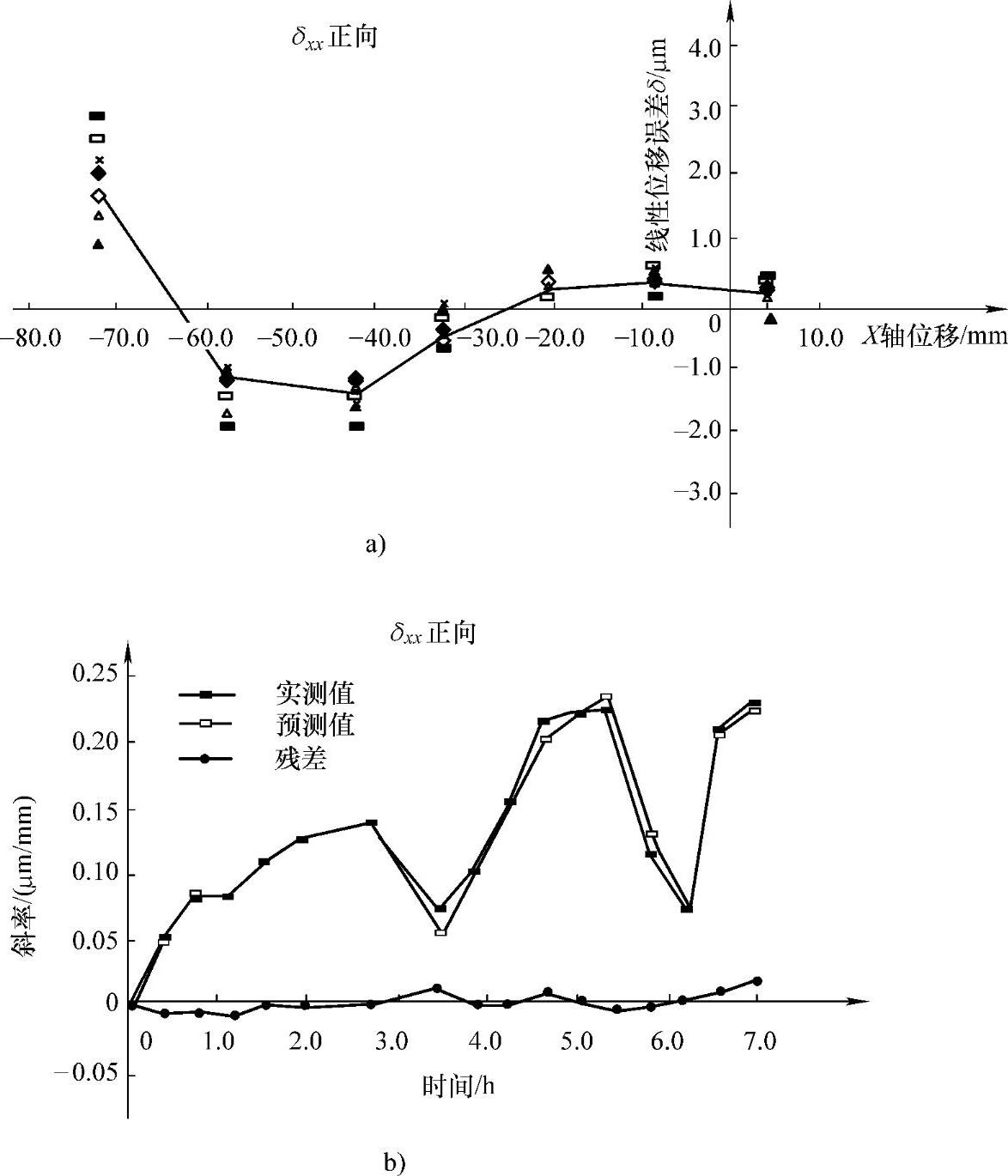
图7-28 X轴线性位移误差的分离

a）几何误差部分建模 b）热误差部分建模

图7-28b所示为热部分，其横坐标为时间t（与机床温度有关），纵坐标为机床不同温度下测得的各线性位移误差曲线的拟合线的斜率。根据与温度和位置坐标都有关的复合误差建模理论，每一次测得的一组误差数据可根据最小二乘法进行直线拟合得一斜率。随着时间的变化或机床温度的上升，拟合直线越来越倾斜，即拟合直线的斜率随着时间或机床温度的变化而变化。经相关计算和分析，对此斜率变化影响最大的温度因素为丝杠温度T₇和螺母温度T₈。故预测值用机床上X轴丝杠相对环境温度的差或变化量ΔT₇（ΔT₇=T₇-T₁₆）和X轴螺母相对环境温度的差ΔT₈（ΔT₈=T₈-T₁₆）线性拟合而成：

δ_xxT（T）=-2.7523×10^-2-4.9600×10^-3ΔT₇+3.3601×10^-2ΔT₈

从图7-28b可见，拟合精度较高，残差仅约0.01μm/mm。

最后再综合几何误差和热误差，则X轴线性位移误差数学模型为

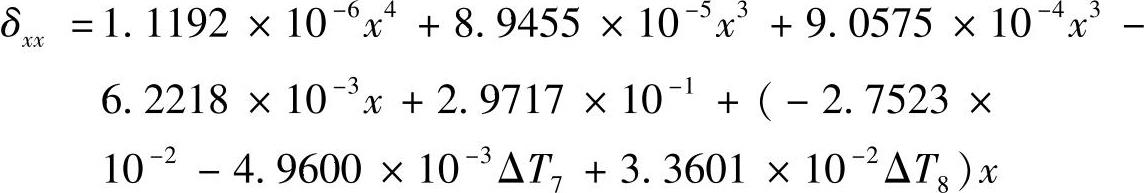
从图7-28可知，X轴线性位移误差数学模型的拟合或预测情况非常好。

2）直线度误差δ_zx。首先在机床冷态下测量直线度误差δ_zx，然后每加热机床1h检测一次。此误差在热循环中变化极小，因此可仅用几何误差数学模型描述它。重复测量三次获得数据后，根据几何误差元素建模理论，可得直线度误差的数学模型为

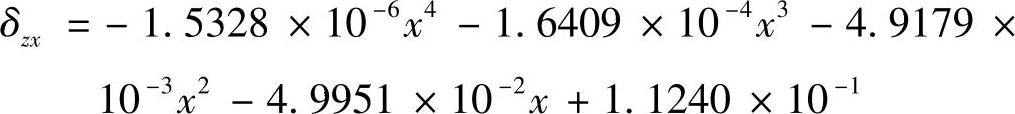
图7-29所示为X轴直线度误差的测量和拟合结果，可见直线度误差数学模型的建模精度较高，最大拟合残差小于0.3μm。

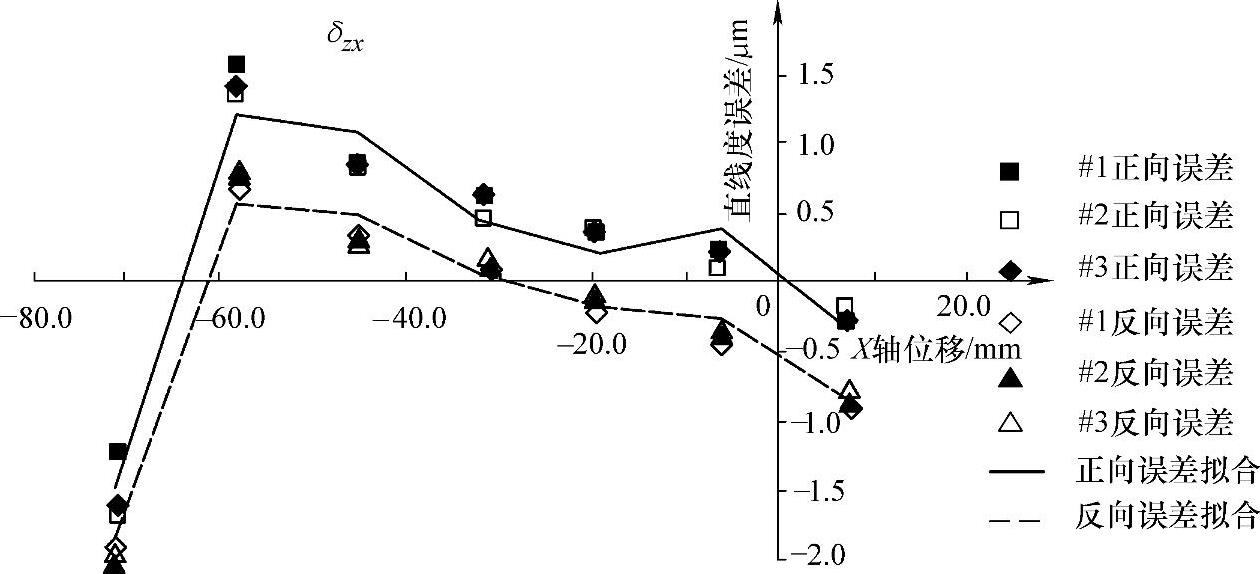
图7-29 X轴直线度误差

3）转角误差ε_yx。同理，机床转角误差ε_yx不随机床热状态的变化而变化（或变化极小），因此也可仅用几何误差数学模型描述。根据误差元素建模理论，可得转角误差的数学模型：

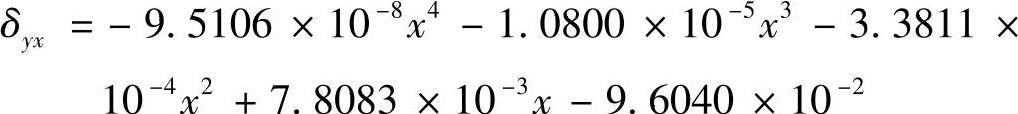
图7-30所示为X轴转角误差的测量和拟合结果。从图7-30可以看出，转角误差数学模型可精确拟合机床转角误差。

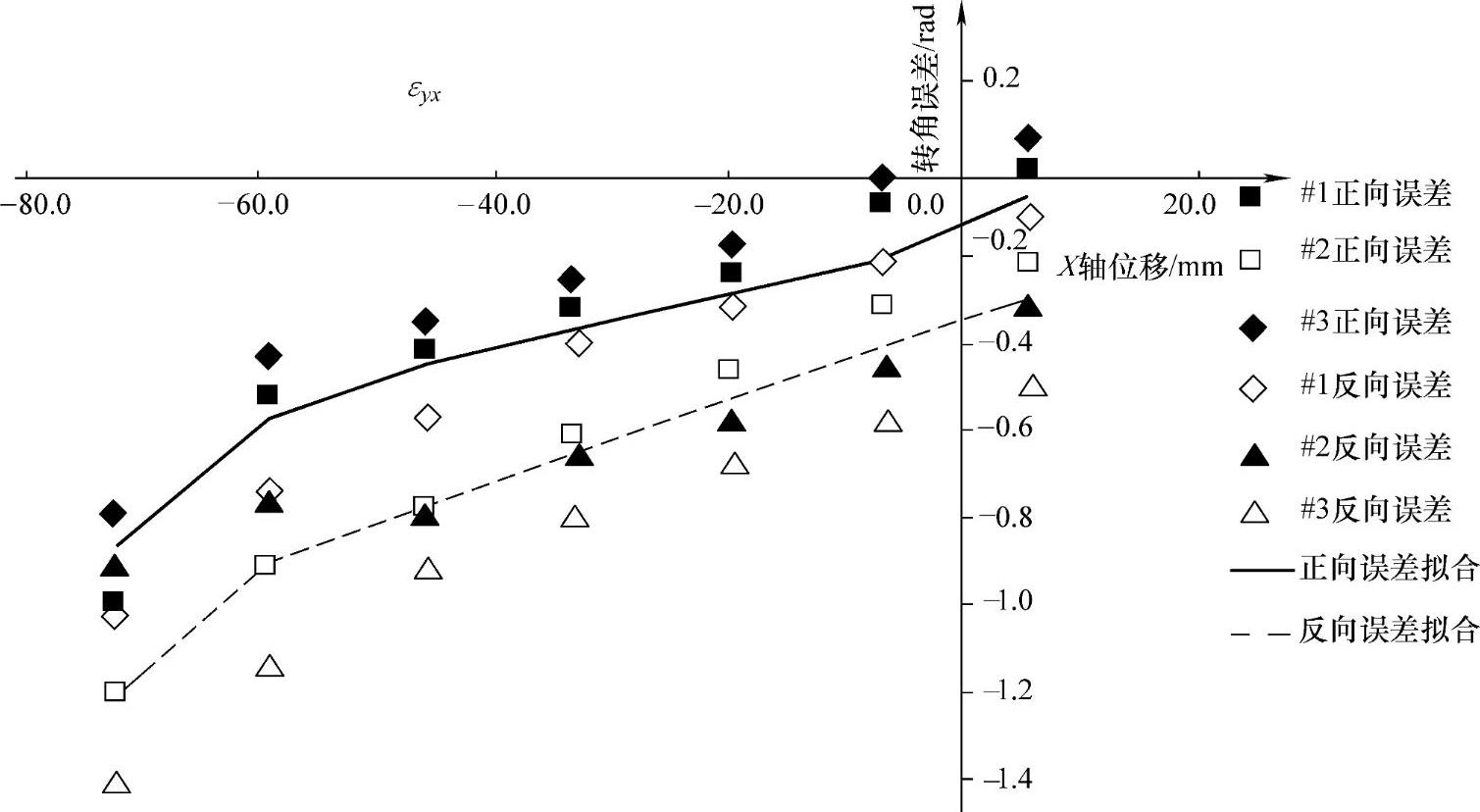
图7-30 X轴转角误差

（2）Z轴误差元素的检测及建模Z轴误差元素的检测、建模方法和X轴误差元素相同。

1）线性位移误差δ_zz

测量Z轴线性位移误差δ_zz时的热循环条件见表7-4，持续时间为6.33h，每20min测量一次。图7-31所示为测定结果（图中仅列部分结果）。

表7-4 Z轴线性位移误差测量中热循环条件

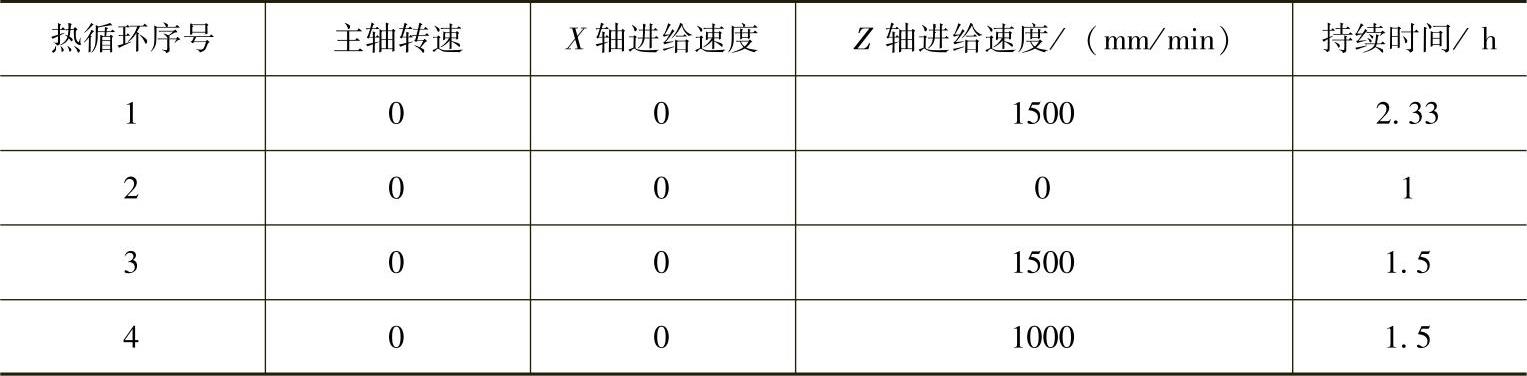
从图7-31可得，随着机床受热温度的升高，误差曲线形状变化不大，而曲线斜率有变化。因此，可将误差元素分离成如下两部分：

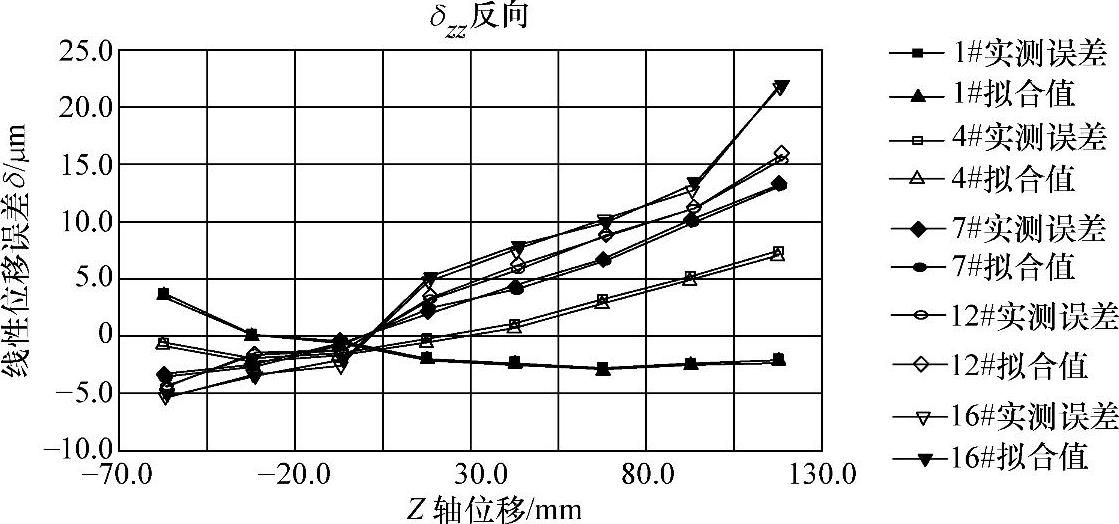
图7-31 Z轴线性位移误差δ_zz

δ_zz（z，T）=δ_zzG（z）+δ_zzT（T）·z

式中 δ_zzG（z）——Z轴线性位移误差元素的几何部分，它只和位置z有关；

δ_zzT（T）——Z轴线性位移误差元素的热部分，它只和温度T有关。

Z轴线性位移误差几何部分和热部分的分离如图7-32所示。其中，图7-32a所示为几何部分，在机床冷态时测得，由几何误差元素建模理论可得几何误差模型：

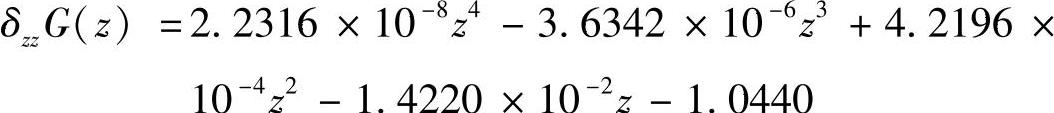
图7-32b所示为热部分，其横坐标为时间t（与机床温度有关）。同理，经相关计算和分析，对此斜率变化影响最大的温度因素为左主轴轴承T₅、右主轴轴承T₆和Z轴螺母T₁₃。故预测值用机床上左主轴轴承相对环境温度的差ΔT₅（ΔT₅=T₅-T₁₆）、右主轴轴承相对环境温度的差ΔT₆（ΔT₆=T₆-T₁₆）和Z轴螺母相对环境温度的差ΔT₁₃（ΔT₁₃=T₁₃-T₁₆）线性拟合而成：

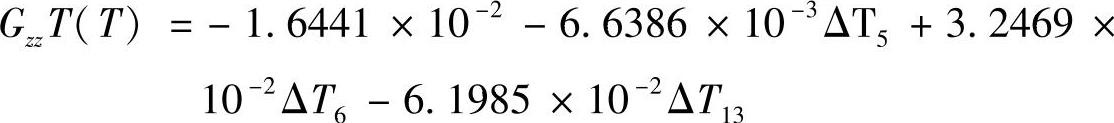
综合几何误差和热误差，则Z轴线性位移误差数学模型为(www.xing528.com)

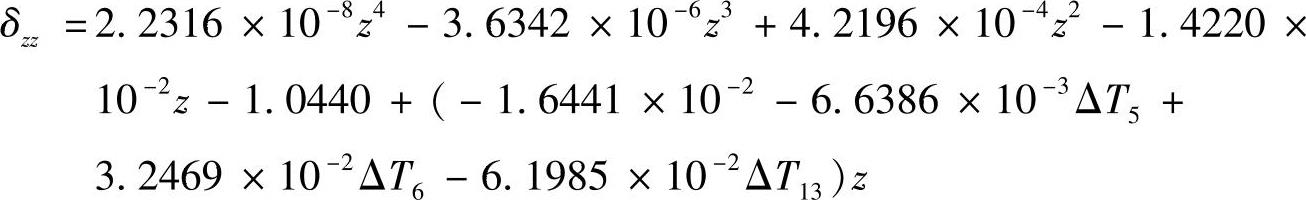
2）直线度误差δ_xz。同理，可知Z轴直线度误差在热循环中变化极小，因此仅用几何模型描述可得直线度误差的数学模型为

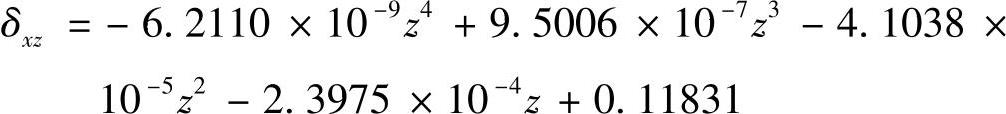
从图7-33可见，直线度误差数学模型有较高的拟合或建模精度。

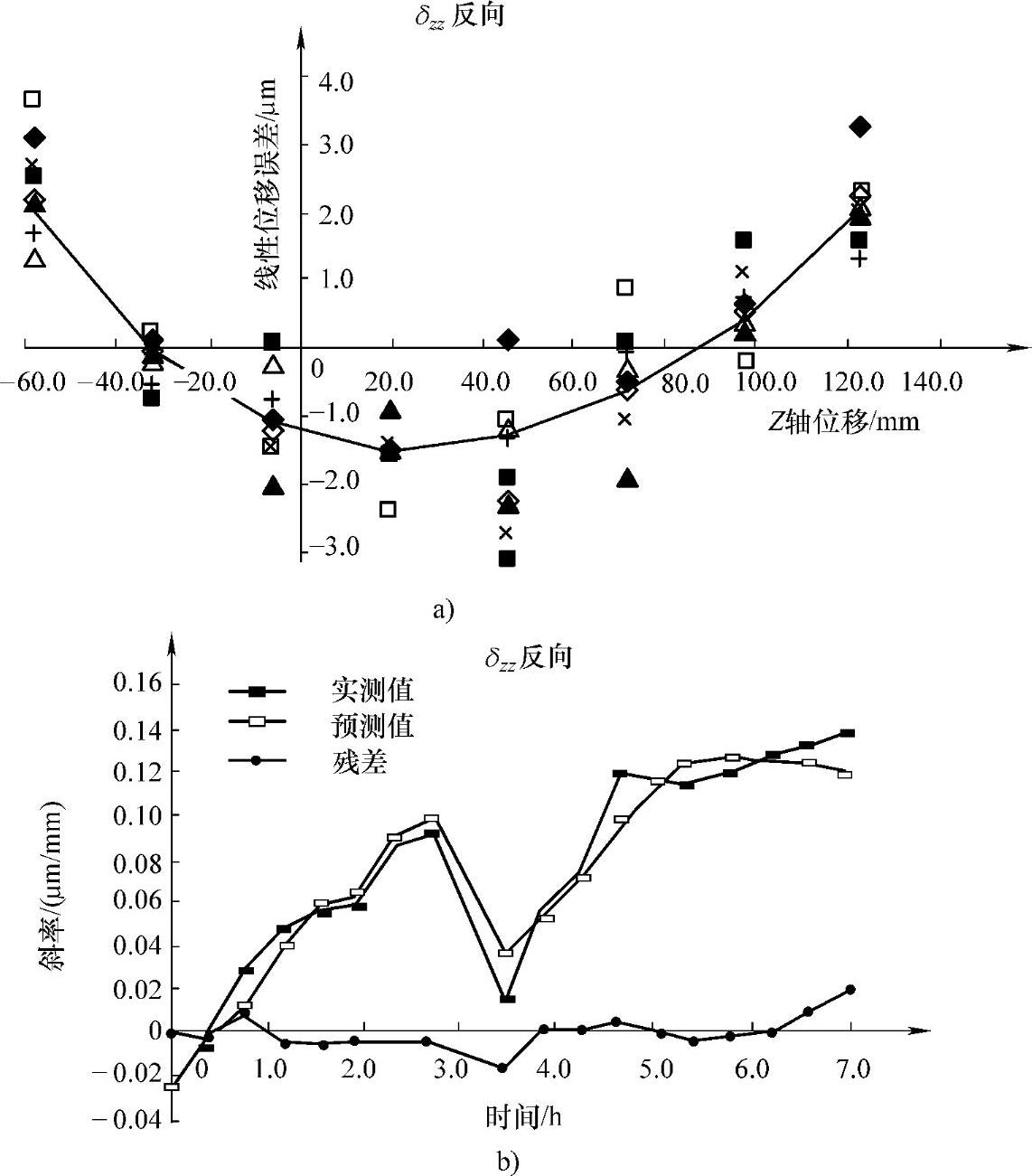
图7-32 Z轴线性位移误差分离

a）几何误差部分建模 b）热误差部分建模

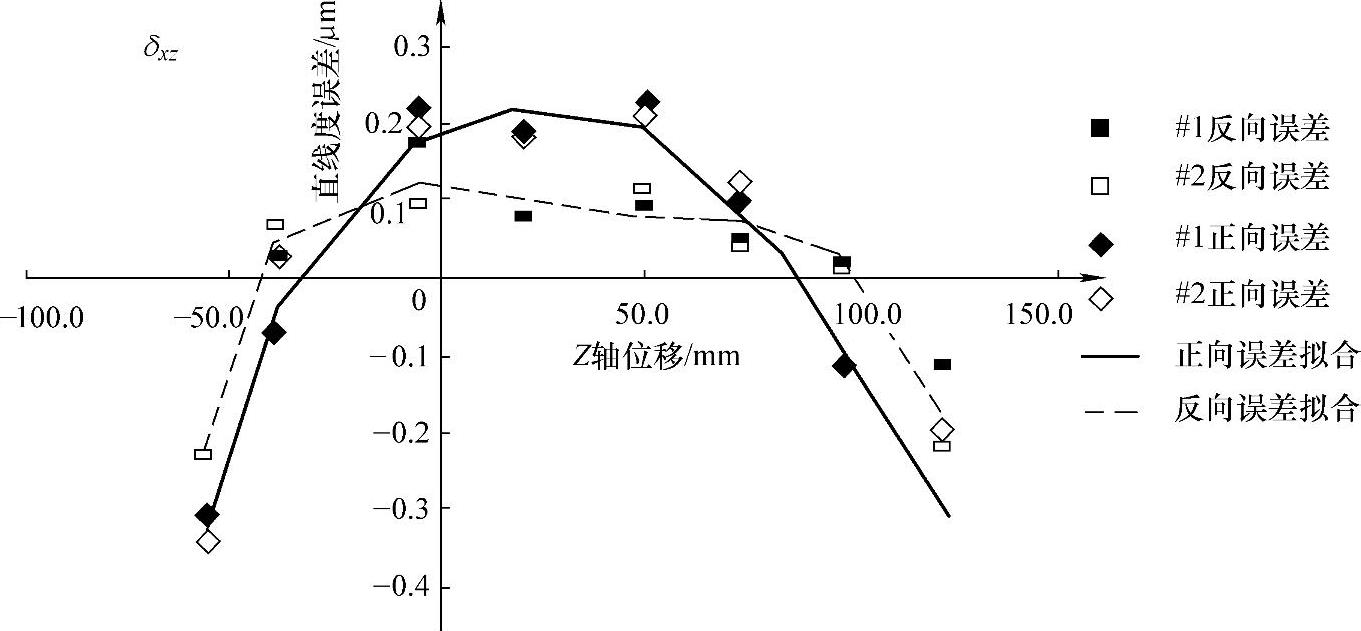
图7-33 Z轴直线度误差

3）转角误差e_yz。图7-34所示为Z轴转角误差测量、建模结果，Z轴转角误差的数学模型为

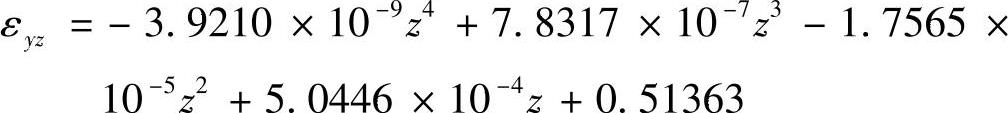
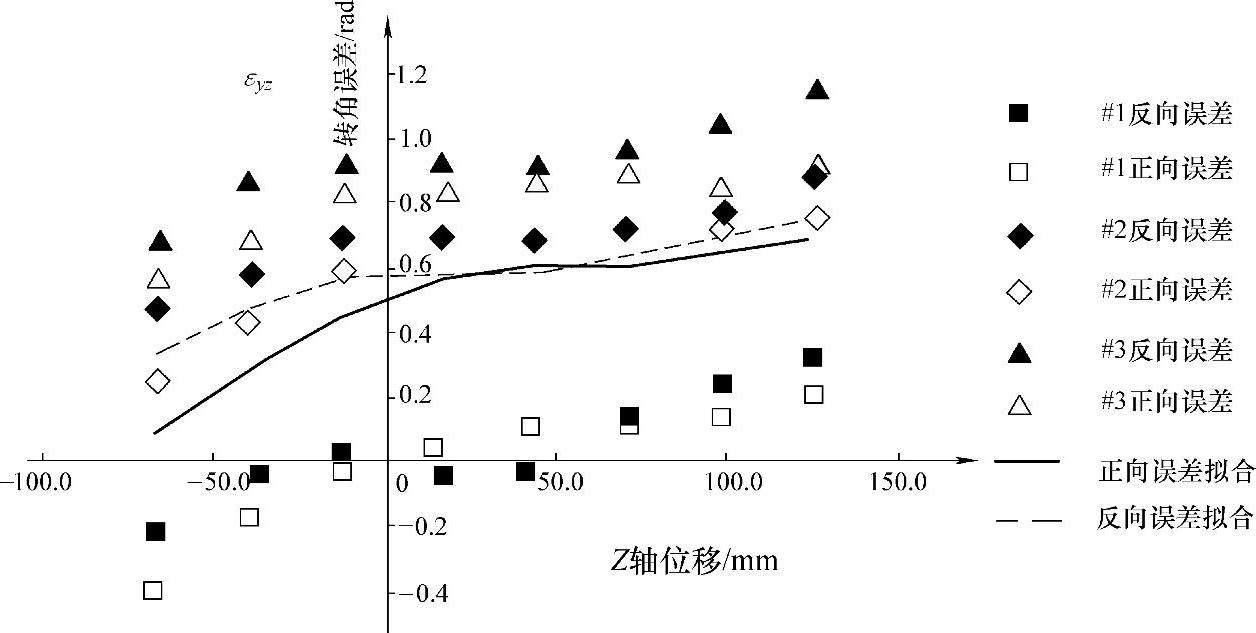
图7-34 Z轴转角误差

（3）其他误差 其他主要影响机床精度的误差元素还有U和W轴的误差元素。由于U、W轴的行程很短，故仅考虑其线性位移（定位）误差。

1）U轴线性位移误差元素δ_xu。U轴线性位移误差元素测量、建模结果如图7-35所示。同理，U轴线性位移误差不随机床温度的变化而变化（或变化极小），因此可以忽略机床温度的影响，而仅建立与坐标位置有关的几何误差数学模型：

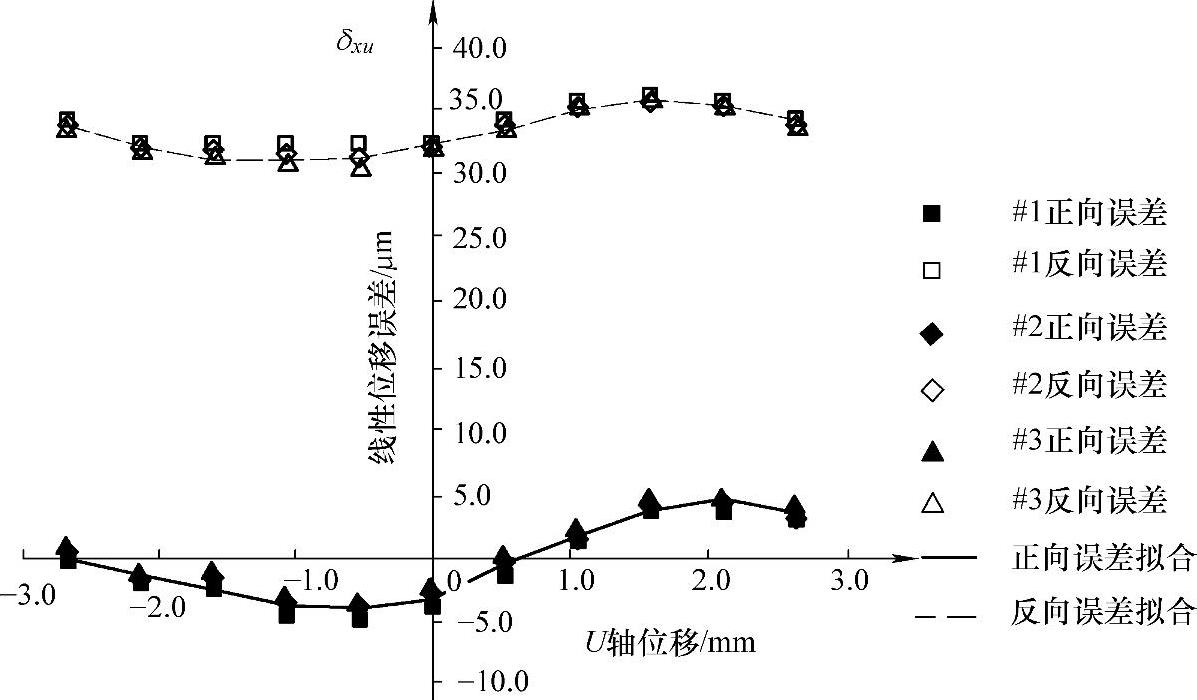
图7-35 U轴线性位移误差

δ_xu=-0.15227u⁴-0.4847u³+1.7931u²+3.8209u-3.1138

2）W轴线性位移误差元素δ_zw。图7-36所示为W轴线性位移误差元素测量、建模结果，同理可得误差数学模型：

δ_zw=3.8688×10^-2w⁴+0.1431w³-0.21723w²-1.2665w-0.81288

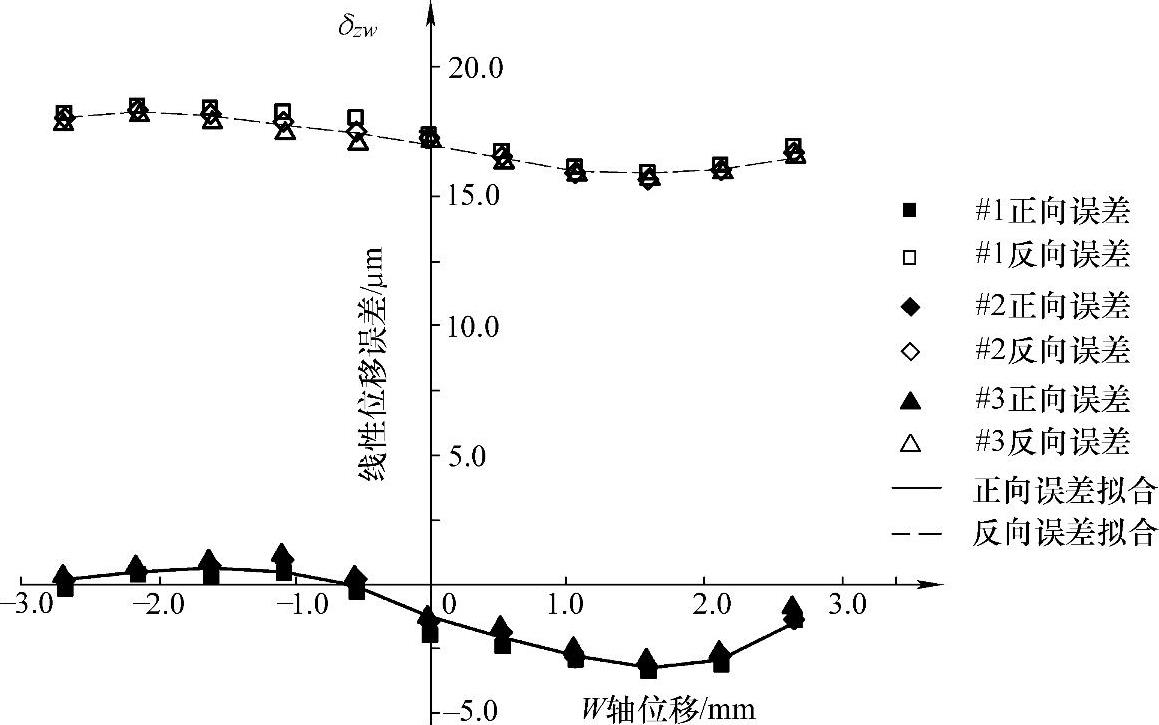
图7-36 W轴线性位移误差

3.与机床工作台位置坐标无关的误差元素检测和建模

（1）垂直度误差S_xz在用激光测量仪检测X轴与Z轴之间的垂直度误差S_xz过程中得知机床温度变化对其影响不大，大约为-25arcsec。

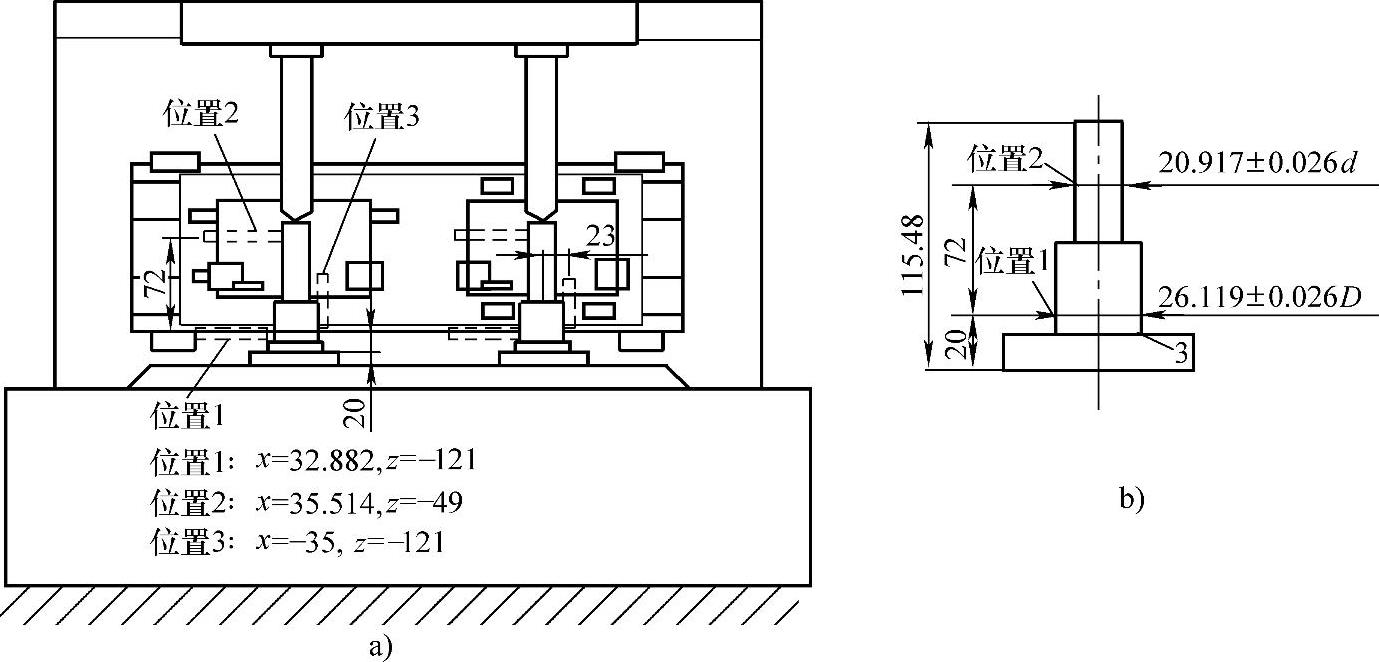
图7-37 电容传感器测热漂移误差

（2）主轴热漂移误差 如图7-37所示，用位移传感器测量系统测量热漂移误差。传感器基座固定在左右两刀架上。图7-37a中的x、z数据表示控制屏幕显示的三个坐标位置。在位置1上测量X方向的热漂移误差，在位置3上测量Z方向的热漂移误差。工件（或测量样件）的尺寸关系如图7-37b所示。

考虑到测量由热变形造成的主轴和Z轴的平行度误差，在位置2上再进行X方向的热漂移误差测量。比较位置1和位置2的读数可计算出平行度误差，即：

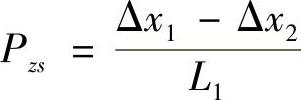
式中P_zs——平行度误差（μrad）；

L₁——位置1与位置2间的距离，本系统设定为72mm。

左、右位置1的读数相当于Δ_sulx或Δ_swrx，左、右位置3的读数相当于Δ_sulz或Δ_swrz。位置1、3的读数表达了机床主轴在X、Z方向的热漂移误差，位置2的读数表达了机床尾架在X方向的热漂移误差。

在表7-5所列的条件下使机床受热升温，间隔一定的时间用电容传感器测量系统测量热漂移误差。测量工况分三种：空切削（机床模拟切削加工循环但不切削工件）、工作台单运动、主轴单运动。另外，考虑到实际应用中的切削情况，在最小二乘拟合建模中除了三种测量工况下获得的数据外还增添了一组机床在生产实际切削加工中获取的工件（见图7-37b）径向尺寸数据（尺寸敏感的X方向）。

表7-5 热漂移误差的检测

1）左主轴在X方向的热漂移误差（位置1）测量和建模。左主轴在X方向的热漂移误差（见图7-37中位置1）测量和建模结果如图7-38所示。经相关性分析等可得左主轴在X方向的热漂移误差与左主轴上轴承T₁、中轴套T₄、X轴螺母T₈、左立柱下T₁₁、左立桥上T₁₂、横桥中T₁₃、左尾架下轴承T₁₄等温度有比较大的关系，建模时采用各温度与环境温度T₁₆的差，应用最小二乘等建模方法可得左主轴在X方向的热漂移误差的数学模型：

Δ₁₁=2.4ΔT₁+1.9ΔT₄+4.3ΔT₈-8.8ΔT₁₁+7.3ΔT₁₂-4.8ΔT₁₃-0.5ΔT₁₄

2）左尾架在X方向的热漂移误差（位置2）测量和建模。左尾架在X方向的热漂移误差（见图7-37中位置2）测量和建模结果如图7-39所示，经相关性分析，左尾架X方向的热漂移误差与左主轴上轴承T₁、X轴螺母T₈、左立桥上T₁₂、横桥中T₁₃、左尾架下轴承T₁₄等温度有比较大的关系，同理可得左尾架在X方向的热漂移误差的数学模型：

Δ₁₂=-3.2-0.4ΔT₁-4.3ΔT₈+6.7ΔT₁₂-6.4ΔT₁₃+6.2ΔT₁₄

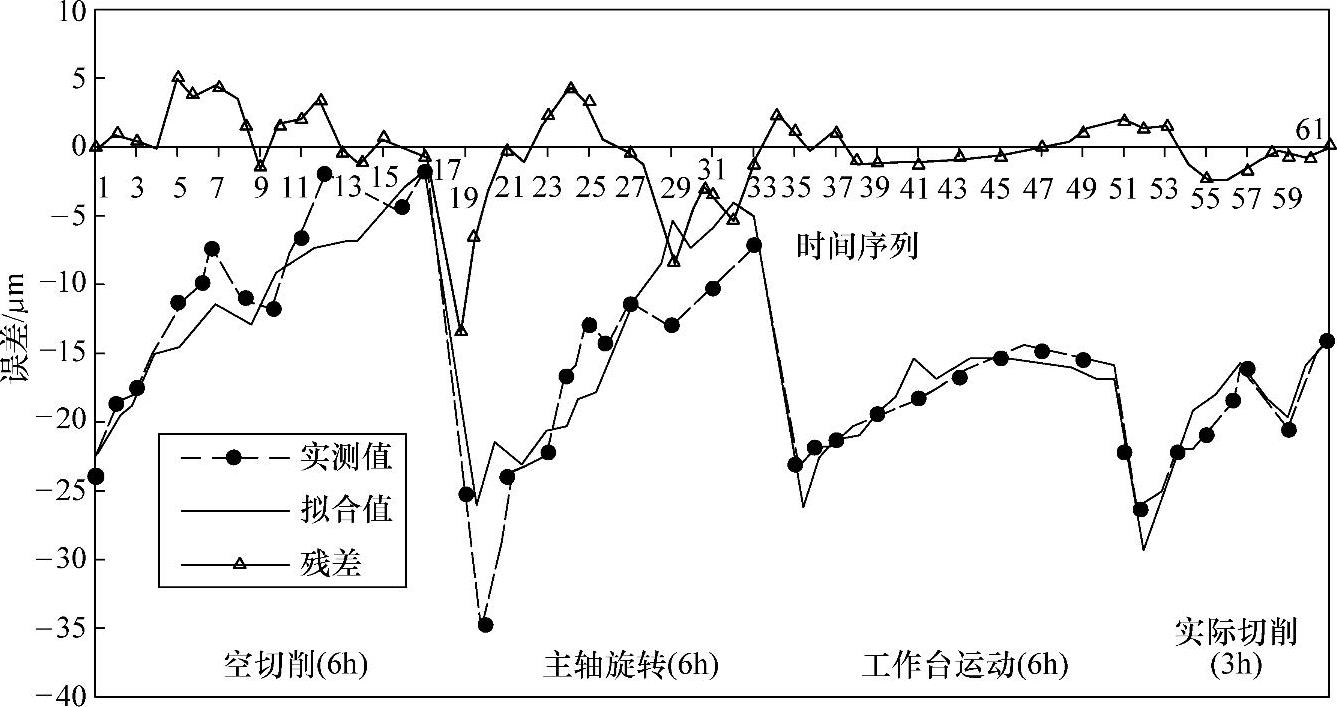
图7-38 左主轴在X方向的热漂移误差

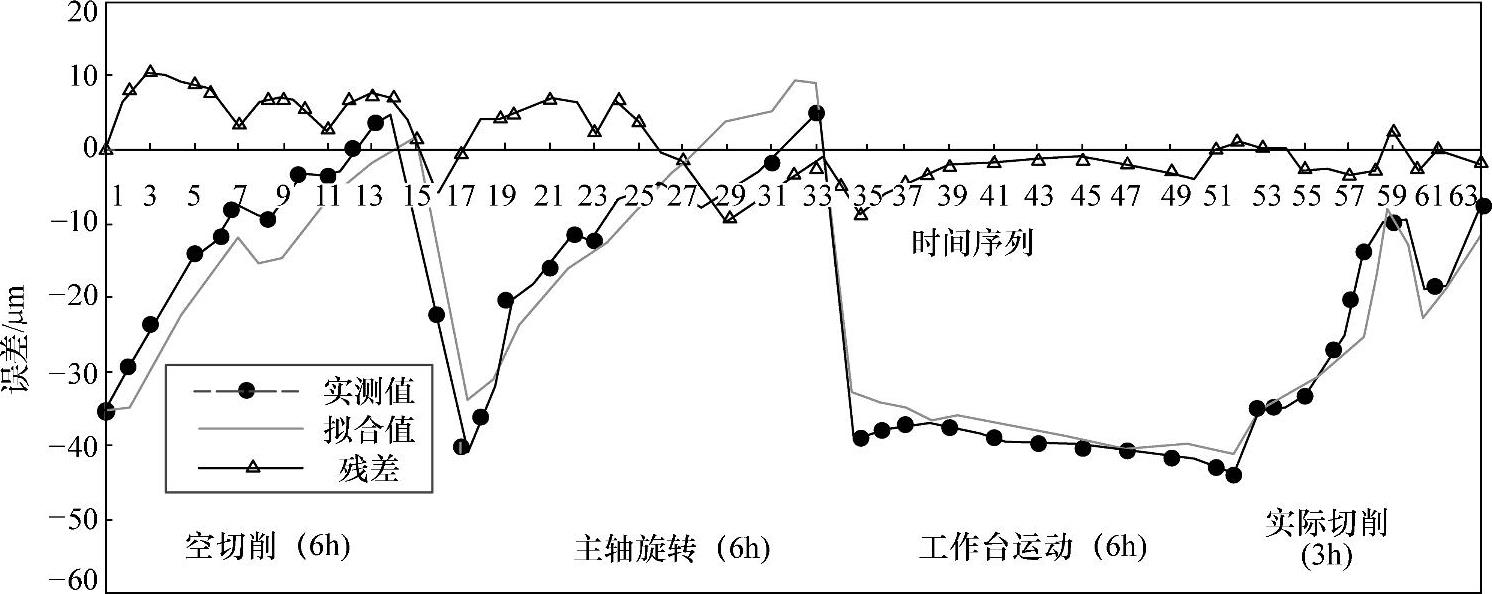
图7-39 左尾架在X方向的热漂移误差

3）左主轴在Z方向的热漂移误差（位置3）测量和建模。左主轴在Z方向的热漂移误差（见图7-37中位置3）测量和建模结果如图7-40所示，经相关性分析，左主轴Z方向的热漂移误差与左主轴上轴承T₁、左主轴下轴承T₃、中轴套T₄、Z轴轴套T₅、Z轴螺母T₆、横桥中T₁₃等温度有比较大的关系，同理可得左主轴在Z方向的热漂移误差的数学模型：

Δ₁₃=-13.5+4.8ΔT₁+3.0ΔT₃+4.2ΔT₄-3.6ΔT₅+5.4ΔT₆-9.7ΔT₁₃

4）右主轴在X方向的热漂移误差（位置1）测量和建模。右主轴在X方向的热漂移误差（见图7-37中位置1）测量和建模结果如图7-41所示，经相关性分析，右主轴X方向的热漂移误差与右主轴上轴承T₂、中轴套T₄、X轴螺母T₈、左立桥上T₁₂、横桥中T₁₃、右尾架下轴套T₁₅等温度有比较大的关系，同理可得右主轴在X方向的热漂移误差的数学模型：

Δr₁=0.3ΔT₂-0.6ΔT₄-2.0ΔT₈-0.7ΔT₁₂+0.4ΔT₁₃-0.5ΔT₁₅

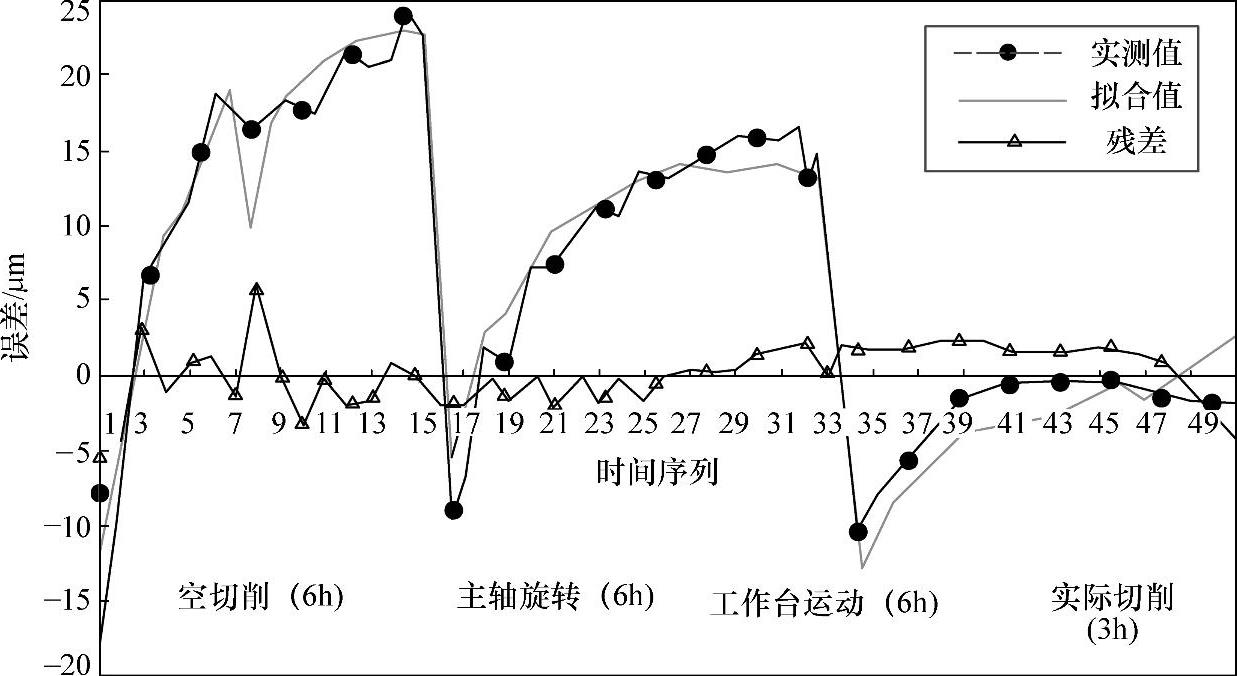
图7-40 左主轴在Z方向的热漂移误差

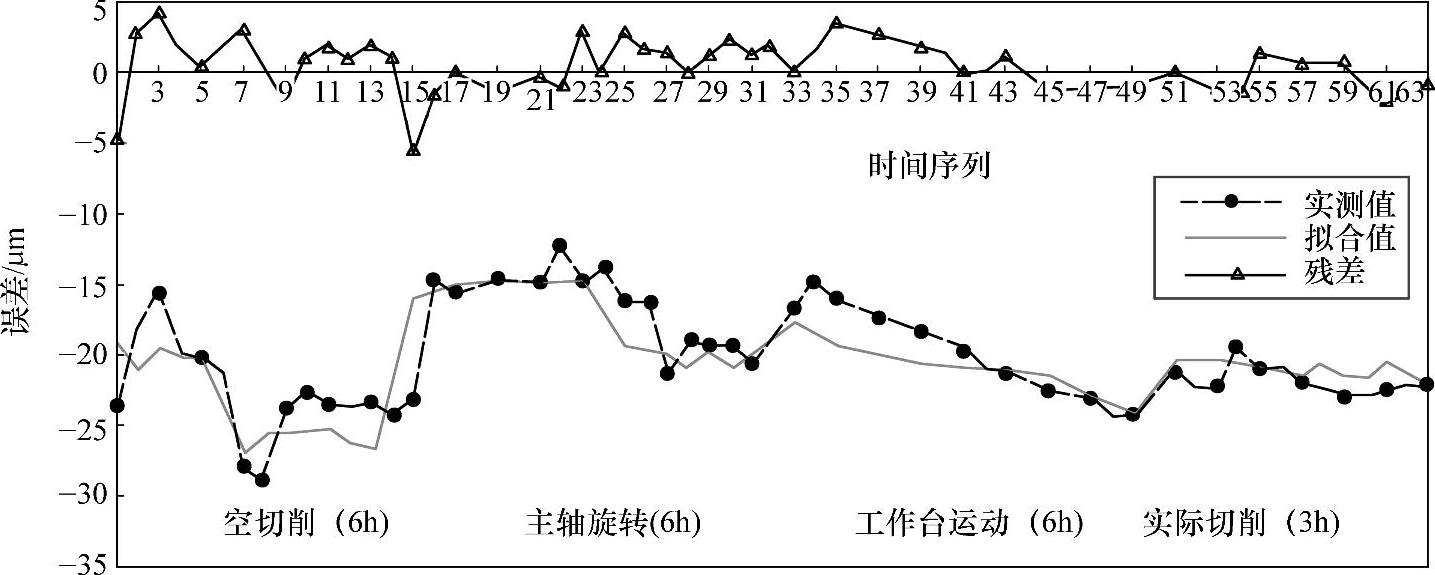
图7-41 右主轴在X方向的热漂移误差

5）右尾架在X方向的热漂移误差（位置2）测量和建模。右尾架在X方向的热漂移误差（见图7-37中位置2）测量和建模结果如图7-42所示，经相关性分析，右尾架X方向的热漂移误差与右主轴上轴承T₂、中轴套T₄、X轴螺母T₈、左立柱下T₁₁、横桥中T₁₃、右尾架下轴套T₁₅等温度有比较大的关系，同理可得右尾架在X方向的热漂移误差的数学模型式如下：

Δr₂=14.1+9.5ΔT₂-8.2ΔT₄-6.9ΔT₈+5.3ΔT₁₁+0.5ΔT₁₃-1.9ΔT₁₅

6）右主轴在Z方向的热漂移误差（位置3）测量和建模。右主轴在Z方向的热漂移误差（见图7-37中位置3）测量和建模结果如图7-43所示，经相关性分析，右主轴Z方向的热漂移误差与右主轴上轴承T₂、左主轴下轴承T₃、左尾架下轴承T₁₄、Z轴轴套T₅、Z轴螺母T₆、W轴轴套T₁₀左立柱下T₁₁等温度有比较大的关系，同理可得右主轴在Z方向的热漂移误差的数学模型：

Δr₃=-2.5-8.4ΔT₂+2.5ΔT₃-4.1ΔT₅+7.5ΔT₆+3.3ΔT₁₀-1.0ΔT₁₁+9.7ΔT₁₄

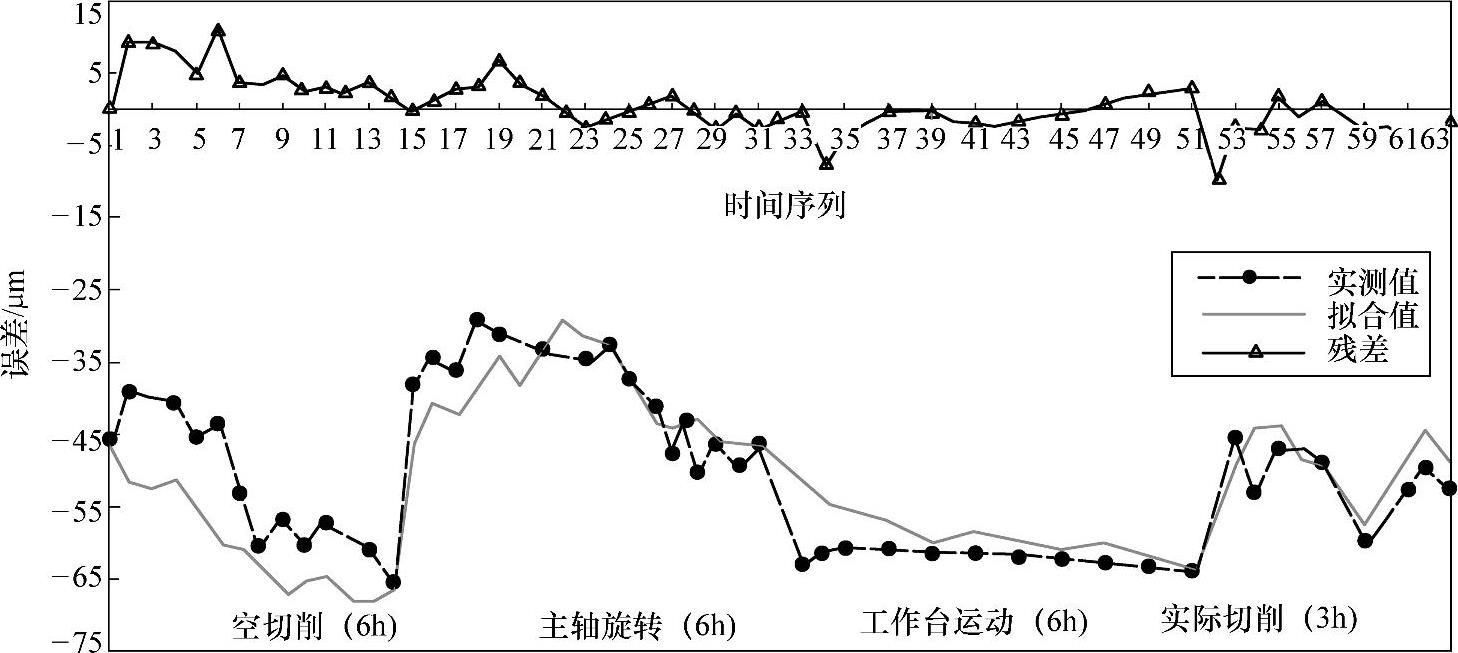
图7-42 右尾架在X方向的热漂移误差

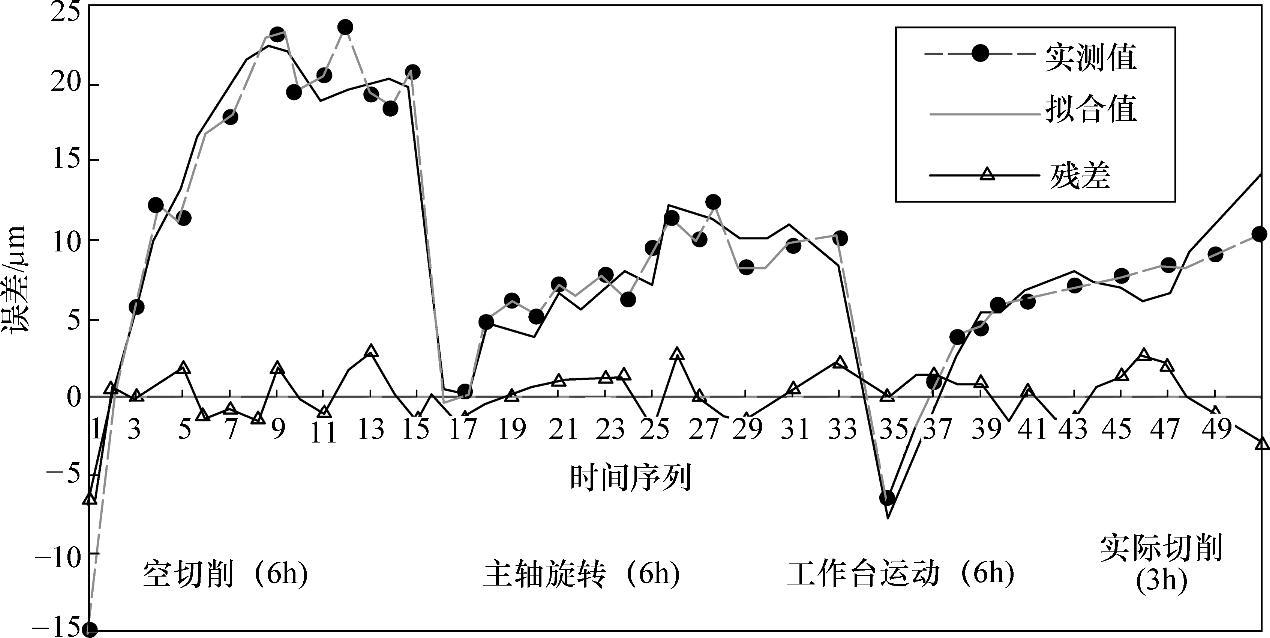
图7-43 右主轴在Z方向的热漂移误差

由图7-38～图7-43可以看出，机床热漂移误差数学模型的拟合精度较好。另外，从应用方便考虑，误差数学模型形式也比较简单，如果需更高的建模精度可选其他一些数学形式或模型。