数学模型综合误差优化

1.设立坐标系和变换矩阵

所设转化坐标系如图7-23所示。根据空间平面坐标系变化公式，考虑到机床角度误差变化很小，得出各变化矩阵。

1）参考坐标系A设在机床床身上，ZA轴平行于大工作台运动轨迹（直线度误差δ_xz）的中心线，XA轴位于Z轴和X轴组成的平面上。

2）坐标系L设在左主轴上，随左主轴移动而移动，ZL轴平行于左工件中心线（左主轴顶尖和左尾架顶尖的连线），XL轴位于Z轴和X轴组成的平面上，故从坐标系L到坐标系A的变换矩阵为

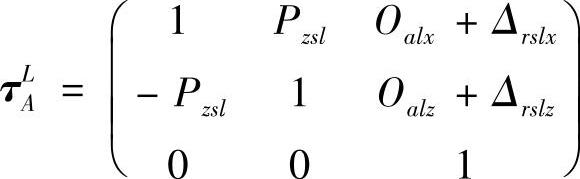
式中 P_zsl——左主轴和ZA轴的平行度误差；

O_alx和Oalz——坐标系A和坐标系L之间X向和Z向的距离。

3）坐标系R设在右主轴上，随右主轴移动而移动，ZR轴平行于右工件中心线（右主轴顶尖和右尾架顶尖的连线），XR轴位于Z轴和X轴组成的平面上，故从坐标系R到坐标系A的变换矩阵为

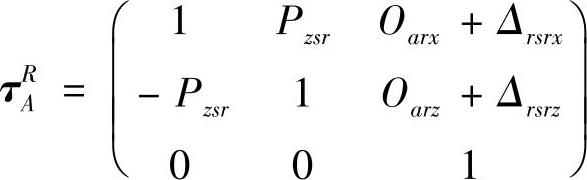
式中 P_zsr——右主轴和ZA轴的平行度误差；

O_arx和O_arz——坐标系A和坐标系R之间X向和Z向的距离。

4）坐标系C设在大工作台（Z轴工作台）上，随大工作台移动而移动，从

坐标系C到坐标系A的变换矩阵为

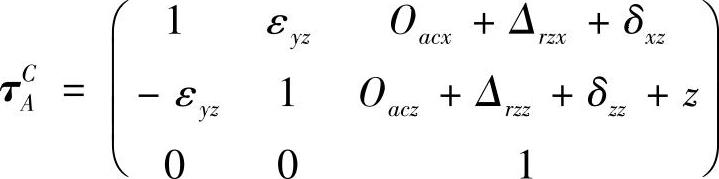
式中 z——大工作台（Z轴工作台）名义位置；

O_acx和Oacz——坐标系A和坐标系C之间X向和Z向的距离；

ε_yz——转角误差；

δ_xz——直线度误差；

δ_zz——大工作台的线性位移误差。

5）坐标系D设在中工作台（X轴工作台）上，随中工作台移动而移动，从坐标系D到坐标系C的变换矩阵为

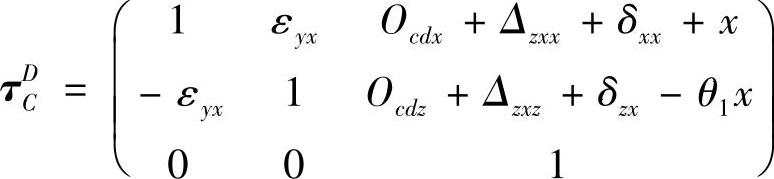
式中 x——中工作台（X轴工作台）名义位置；

O_cdx和O_cdz——坐标系C和坐标系D之间X向和Z向的距离；

θ₁——中工作台直线度误差δ_zx的中心线和XC轴（坐标系C的X轴）角度误差。

由于δ_xz的中心线平行于ZA轴，于是当Z=0时有δ_zx的中心线和ZC轴（坐标系C的Z轴）之间的角度等于-ε_yz（0）。又垂直度误差S_xz定义为二直线度误差δ_zx、δxz的两根中心线之间夹角和直角的差。因此，有

S_xz=θ₁+ε_yz（0）θ₁=S_xz-ε_yz（0）

6）坐标系E设在左小工作台（U轴工作台）上，随左小工作台移动而移动，从坐标系E到坐标系D的变换矩阵为

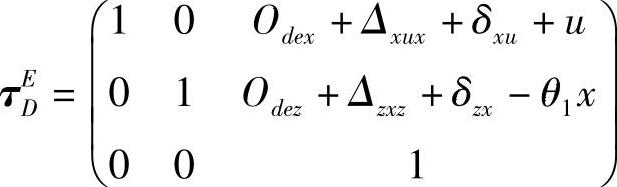
式中 u——左小工作台（U轴工作台）名义位置；

O_dex和O_dez——坐标系D和坐标系E之间X向和Z向的距离。因为U轴的行程比较短（为25mm），故转角误差、直线度和平行度可忽略。

7）坐标系F设在右小工作台（W轴工作台）上，随右小工作台移动而移动，从坐标系F到坐标系D的变换矩阵为

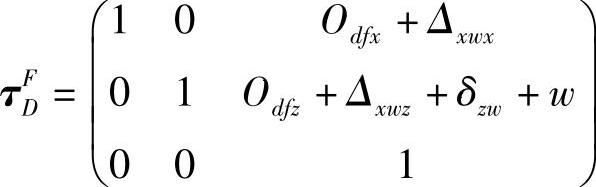
式中w——左小工作台（W轴工作台）名义位置；

O_dfx和O_dfz——坐标系D和坐标系F之间X向和Z向的距离。

因为W轴的行程比较短（为25mm），故转角误差、直线度和平行度忽略。

8）设相对于坐标系E、F（为左右二刀架基座）的左、右二边刀尖的位置分别为

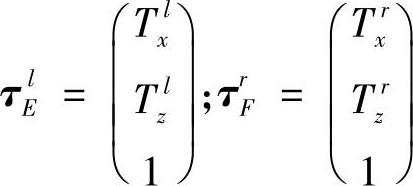
则相对于参考坐标系A的左、右二边刀尖位置为

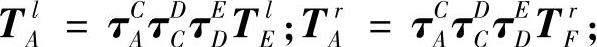
2.误差综合数学模型(www.xing528.com)

通过把左右两刀尖坐标位置从刀架基座坐标系（E、F）变换到工件坐标系（L、R）并设定所有误差为零，则可得左右两刀尖相对于工件的理想坐标位置为

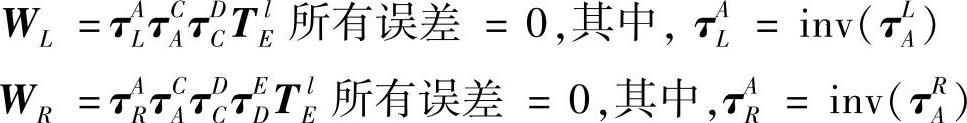
因此可得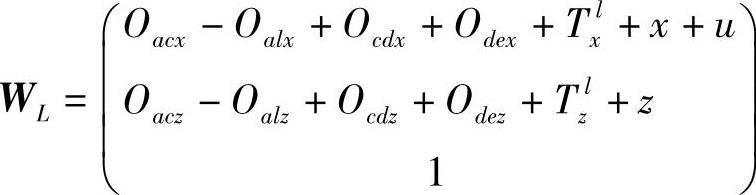

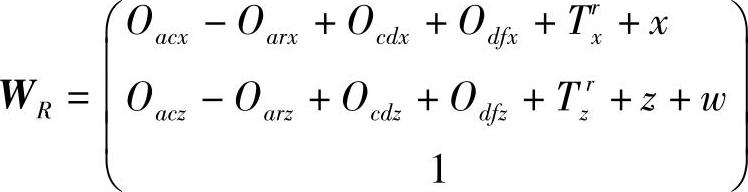
在参考系A中，比较刀尖实际位置和理想位置，则可得误差综合数学模型（或称综合误差）为

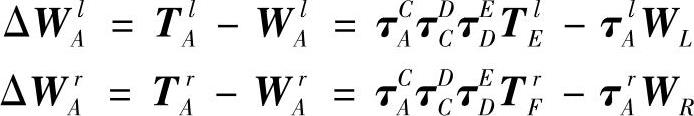
代入各变换矩阵，整理后可得左主轴综合误差和右主轴综合误差。

对于左主轴，X、Z两个方向的综合误差分别为

对于右主轴，X、Z两个方向的综合误差分别为

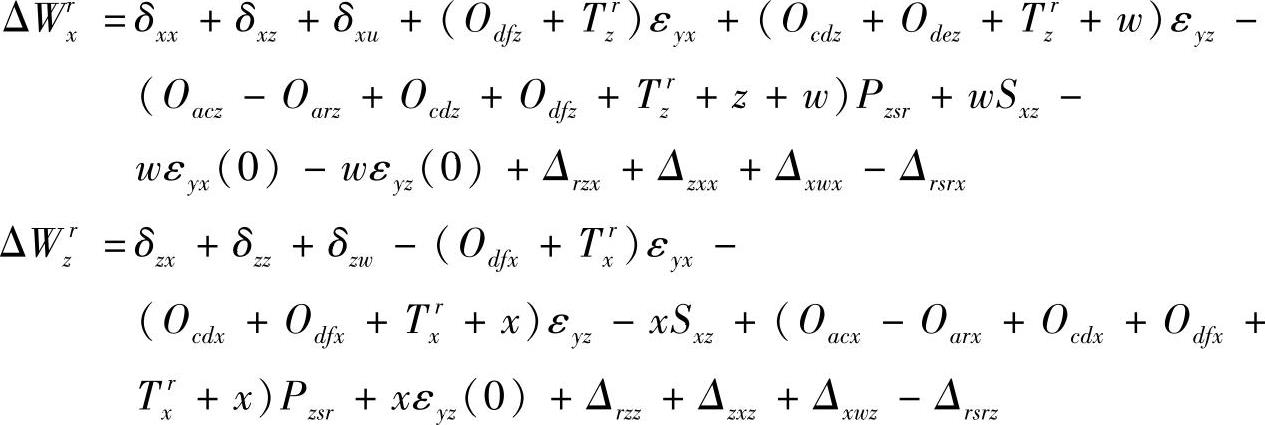
综合误差公式包含了23个误差因子。因为U、W轴行程仅25mm，故其直线度误差、转角误差和平行度误差忽略。

3.几何和热误差综合数学模型的简化

上面已得综合误差公式，但公式中一些常数或系数需通过测量坐标系的设立等来确定。对于本机床，考虑到测量方便及一般加工工件形状尺寸等因素，所设测量坐标系如图7-24所示。

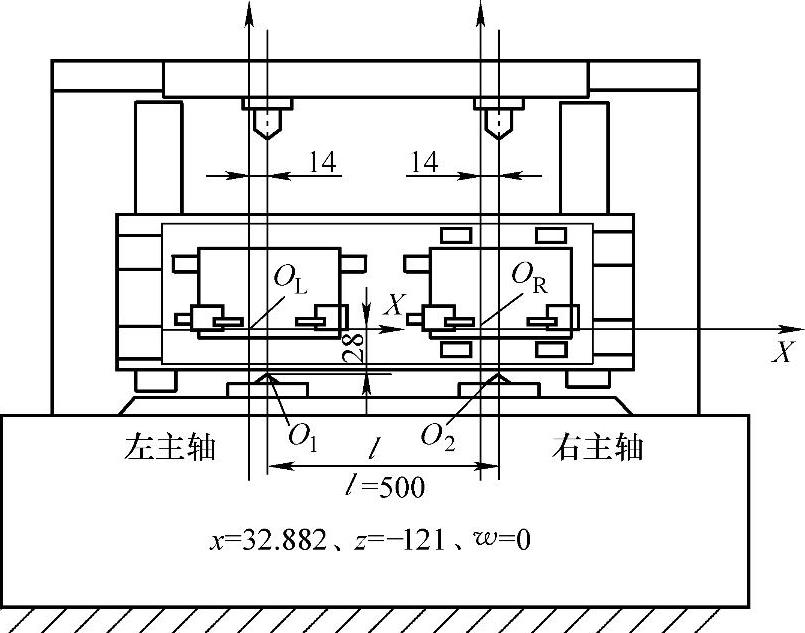
图7-24 测量坐标系

1）坐标说明如下：

①O_L为左主轴坐标系L的原点，距左主轴中心线左14mm、左主轴顶尖（O₁）上28mm。

②O_R为右主轴坐标系R的原点，距右主轴中心线左14mm、右主轴顶尖（O₂）上28mm。

③运动U、W轴工作台至零位（u=w=0），运动X、Z轴工作台至控制器读数x=32.882、z=-121，调整左、右刀尖位置分别与O_L、O_R两点重合。此时位置就是测量系统的零位（当工作台或刀架移动至最上最左时，为机床位置的零位）。

④各坐标原点O_A、O_C、O_D和O_E设置重合于O_L点位置，因此有O_ALX=O_ALZ=OACX=OACZ=OCDX=OCDZ=ODEX=ODEZ=0。

⑤O_F设置重合于O_R点位置，因此有O_ALX=l、O_DFX=l、O_ARZ=O_DFZ=0，其中，L为二主轴之间距离。

把上面选择的常数代入综合数学模型可得

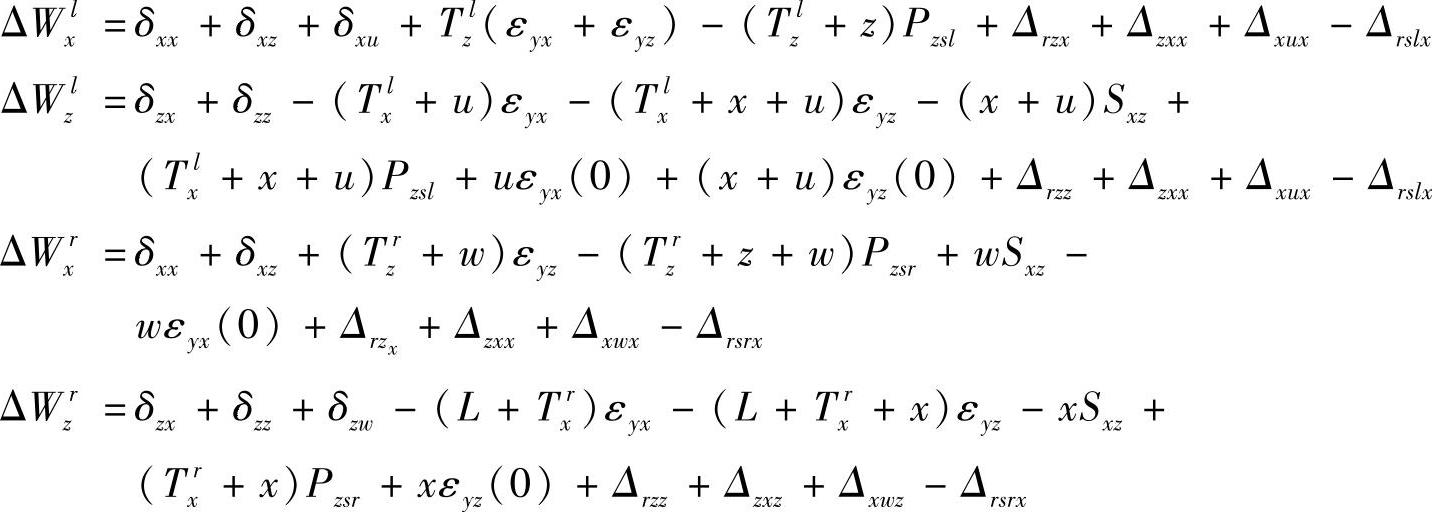
2）误差综合模型可进一步简化如下：

①由于u和w仅用于误差补偿而不用于切削加工循环，故它们的值很小。因此，u和w及沿此二轴的误差元素都可忽略。

②由于X轴直线度小于±0.4μm，Z轴直线度小于±1.5μm，故可忽略。

③由于刀具坐标系的原点（O_L和O_R）位于刀尖上，故有

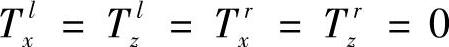
④原点热漂移和主轴热漂移具体测量计算如下：

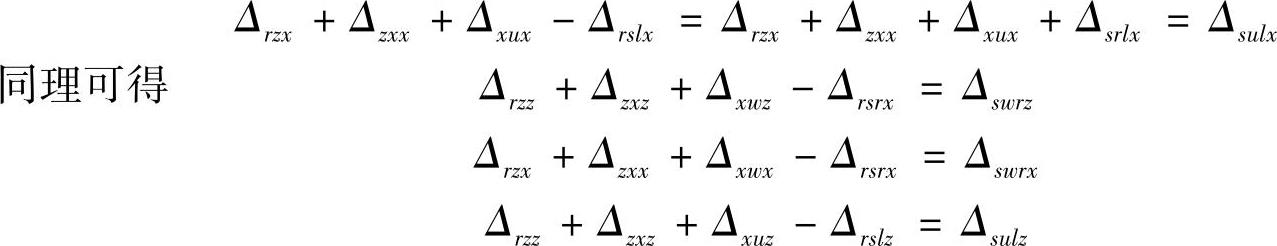
而Δ_sulx、Δ_sulz、Δ_swrx、Δ_swrz为左、右小工作台（刀架）相对于左、右主轴（工件）的热漂移误差。只要把位移传感器的基座固定在刀架上测主轴或工件，即可得到这些位移。然后，结合机床各点温度数据，根据多元回归理论进行误差模型的拟合。

最后可得

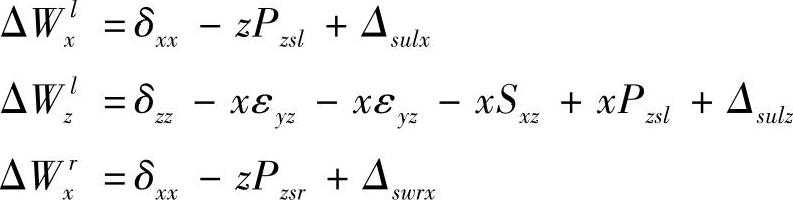
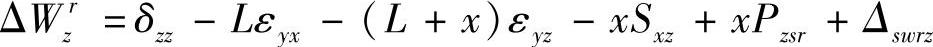
3）有关符号说明如下：

①如果刀尖相对于工件作接近运动，则ΔW为正。

②如果U或W坐标系的原点相对于左或右主轴作接近运动，则Δ_sul或Δ_swr为正。

③如果主轴中心线S位于Z轴的右边，则两轴平行度P_zs为正，否则为负。