机床几何与热误差建模：以实际加工误差为建模数据

1.车削中心的误差综合数学模型

（1）坐标系的设定 机床结构简图及所设坐标系如图7-14。所设坐标系描述如下：

1）坐标系r设在机床上，为参考坐标系（固定坐标系）。

2）坐标系s设在主轴上，随主轴热变形而移动。

3）坐标系c设在工作台上，随工作台沿Z轴运动（包括工作台热变形产生的运动）而移动。

4）坐标系t设在刀架上，随工作台沿X轴运动（包括刀架热变形产生的运动）而移动。

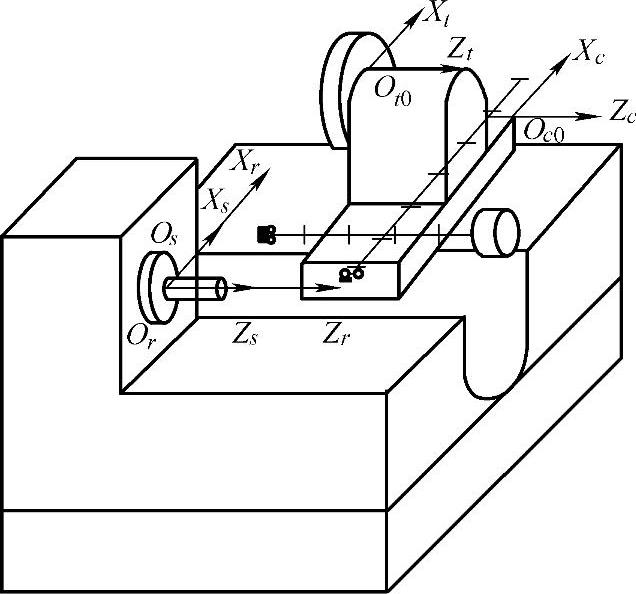
图7-14 车削中心结构简图及坐标系

（2）误差元素分析 本机床为平面误差，所有误差产生在ZX平面，影响机床精度的主要误差元素有如下14个：

1）有关Z轴的误差，包括定位误差δ_zz、直线度误差δ_xz、转角误差ε_βz，以及工作台坐标系c原点相对于参考坐标系r沿X、Z方向的热漂移Δ_rcx和Δ_rcz。

2）有关X轴的误差，包括定位误差δ_xx、直线度误差δ_zx、转角误差ε_βx，以及刀架坐标系t原点相对于工作台坐标系c沿X、Z方向的热漂移Δ_ctx和Δ_ctz。

3）有关主轴的误差，包括主轴沿Z、X方向的热漂移误差（主轴热变形）Δ_rsx和Δ_rsz，以及主轴和Z轴的平行度误差η_sz。

4）其他误差，如Z轴和X轴的垂直度误差η_zx。

（3）误差运动综合模型 先把刀尖坐标表达在其所在坐标系（刀架坐标系）中，再根据齐次坐标转化原理转化到参考坐标系。然后，把工件上正在被切削点的坐标表达在其所在坐标系（主轴坐标系）中，同理转化到参考坐标系。根据刀尖和工件上正被切削点位于空间同一点，得这两部分的等式。最后，求解等式可得几何和热误差综合数学模型。

1）有关刀尖位置数学模型：

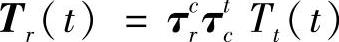
式中T_r（t）——在参考坐标系r的刀尖位置矢量；

τ^t_c——从刀架坐表系t到工作台坐标系c的转化矩阵；

τ^c_r——从工作台坐表系c到参考坐标系r的转化矩阵；

T_t（t）——在刀架坐表系t的刀尖位置矢量。

2）有关工件位置数学模型：

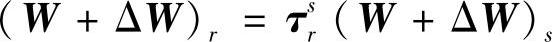
式中W——工件理想尺寸矢量；

ΔW——工件尺寸误差矢量；

（W+ΔW）r——在参考坐标系r中的工件尺寸矢量；

τ^s_r——主轴坐标系s到参考坐标系r的转化矩阵；

（W+ΔW）s——在主轴坐标系s中的工件尺寸矢量（工件实际尺寸矢量）。

3）误差综合模型。由于刀尖和工件上正被切削点在同一点位置，所以有

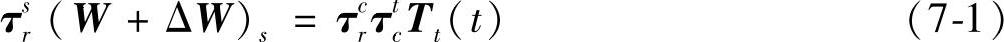
求解式（7-1）可得工件尺寸误差（或误差运动）矢量ΔW。

假设机床没有任何误差，则易得

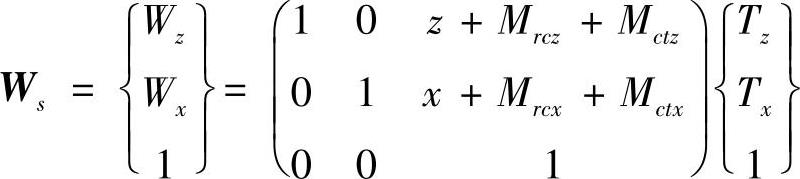
式中W_z、W_x——工件轴向、径向的理想尺寸；

z、x——工作台Z轴方向、刀架X轴方向的运动行程；

M_rcz、M_rcx——参考坐标系与工作台坐标系原点之间Z向、X向的距离；

M_ctz、M_ctx——工作台坐标系与刀架坐标系原点之间Z向、X向的距离；

T_z、T_x——刀尖在刀架坐标系中的位置。

根据齐次坐标变化基本原理，可得

式中η_rs——主轴相对于参考坐标轴Z_r的平行度误差。

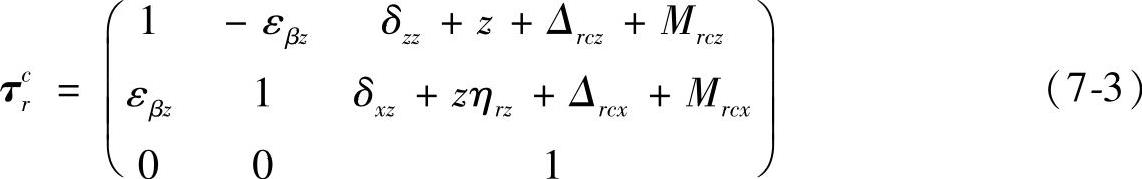
式中η_rz——Z运动轴相对于参考坐标轴Z_r的平行度误差，η_sz=η_rz-ηrs

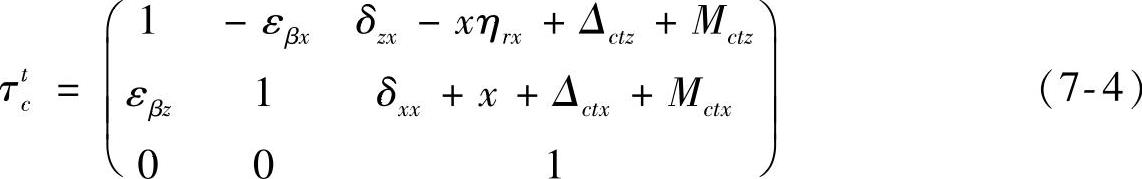
式中η_rx——X运动轴相对于参考坐标轴Z_r的垂直度误差，η_sx=η_rx-ηrs。

整理式（7-1）～（7-4）可得

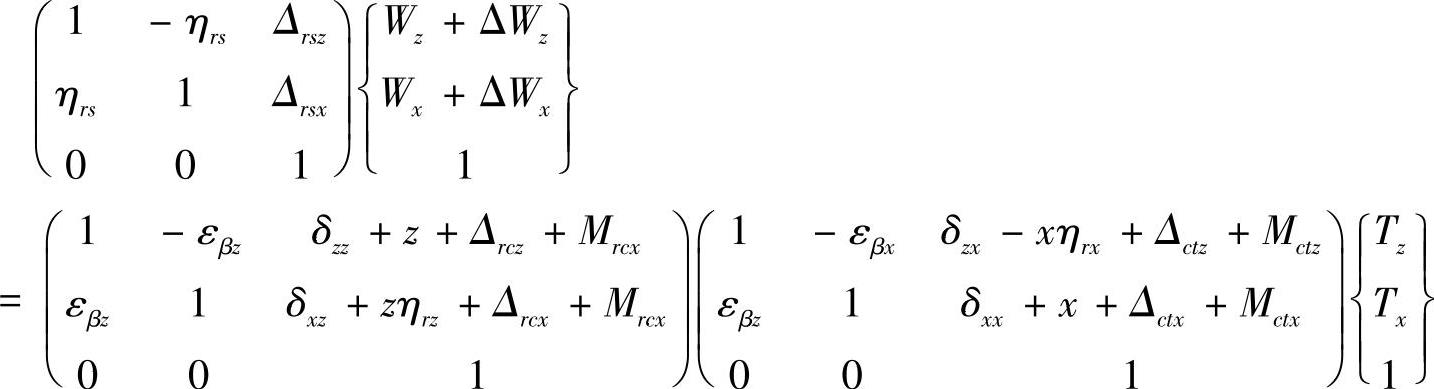(www.xing528.com)

整理上式并忽略高阶量，有

ΔWz=δzx+δzz-（ηsx+εβz）x-（εβz+εβx-ηrs）Tx-（εβz-ηrs）Mctx+Mrcxηrs+Δstz

ΔWx=δxx+δxz-ηszz+（εβz+εβx-ηrs）Tz-（εβz-ηrs）Mctz+Mrczηrs+Δstx

式中Δ_stz=Δ_rcz+^Δ_ctz-Δrsz，Δstx=Δrcx^+Δctx^-Δrsx；

Δ_st是由机床热变形引起的刀具相对于主轴或工件的位移误差，直接反映了加工精度或工件尺寸的变化。在试验中，Δ_st可通过把位移传感器基座固定在刀架上测主轴而获得。

图7-15所示为机床几何误差和热误差运动矢量关系图。

2.车削中心热误差模型

经检测和分析，对所研究的车削中心，与机床运动位置有关的几何误差不大于10μm，而与机床温度有关的热误差（大约40μm）占了总误差的75%，故这里只考虑热误差元素的建模和补偿。

热误差最主要应为机床温度分布的函数，故机床的类型、大小、结构，加工工件的材料、形状、大小，刀具的材料、形状等因素都间接通过机床温度分布来影响机床热变形。故热误差数学模型的一般形式（热误差数学模型的形式可以有许多，这里仅以较简单明了的一般形式为例）可为

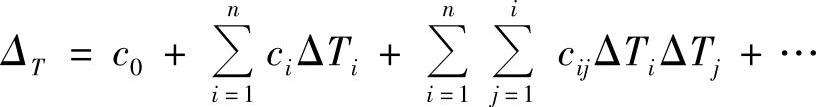
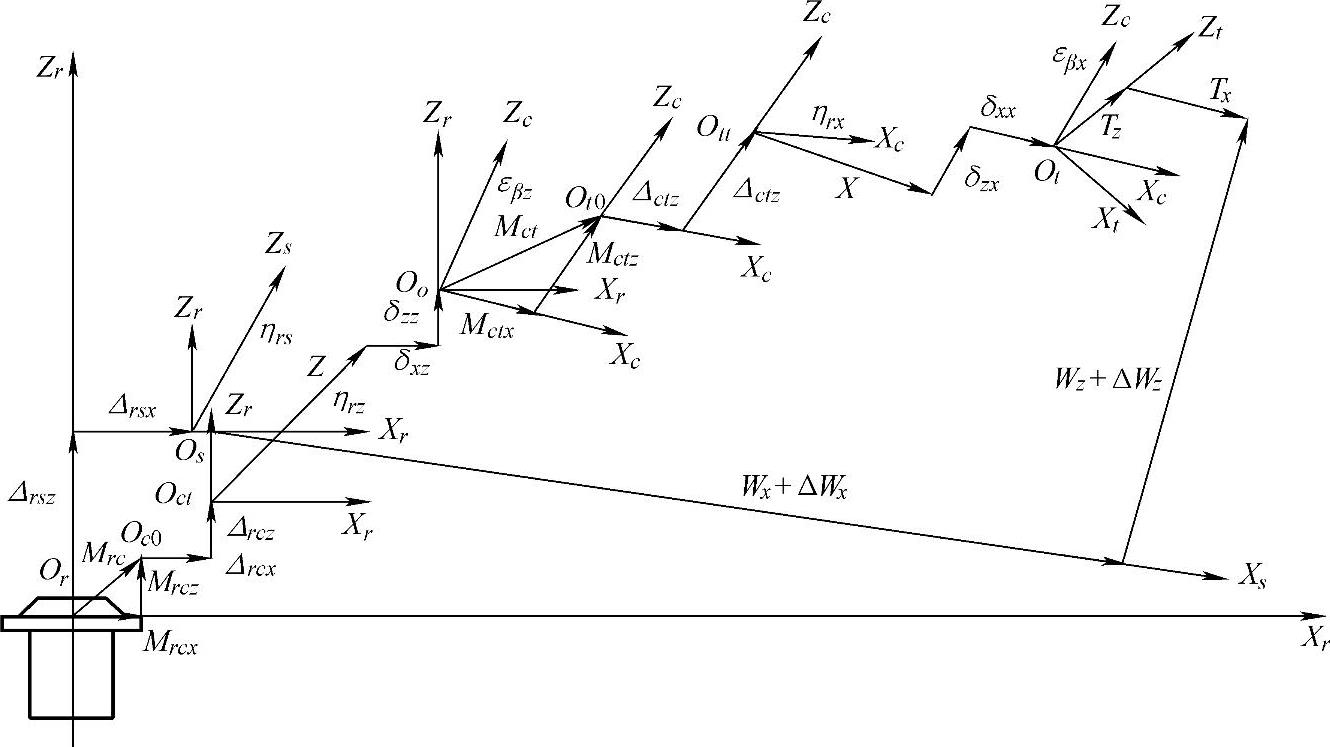
图7-15 机床几何误差和热误差运动矢量关系图

式中Δ_T——热误差；

c₀、c_i、cij——模型的温度系数；

ΔT_i、ΔT_j——温度变量。

（1）热误差建模的一般过程 热误差建模一般过程如下：

1）采集机床各关键点温度数据和相应时间的热误差数据。

2）选择热误差数学模型的阶数或其他数学模型形式。

3）使用最小二乘拟合法或其他方法确定参数。

4）计算拟合残差，如果精度不够，提高模型阶数重新拟合直至符合要求。

考虑到工厂实际使用的方便性，这里的热误差模型估计式设定为线性模型。另外，为使建模条件接近实际加工条件及在建模过程中不影响工厂生产，实际加工后的工件尺寸误差作为热误差被用为建模数据。

在机床关键温度点的优化选择中，根据优化布置策略，先后使用了主因素策略、互不相关策略、最近线性策略、最少布点策略等，获得了与上节所述的热变形模态分析中得出一致的在车削中心上的四个关键温度点，并将其用于热误差建模。最终从16个温度传感器减少到仅使用四个。图7-16所示为机床四个关键点温度变化。

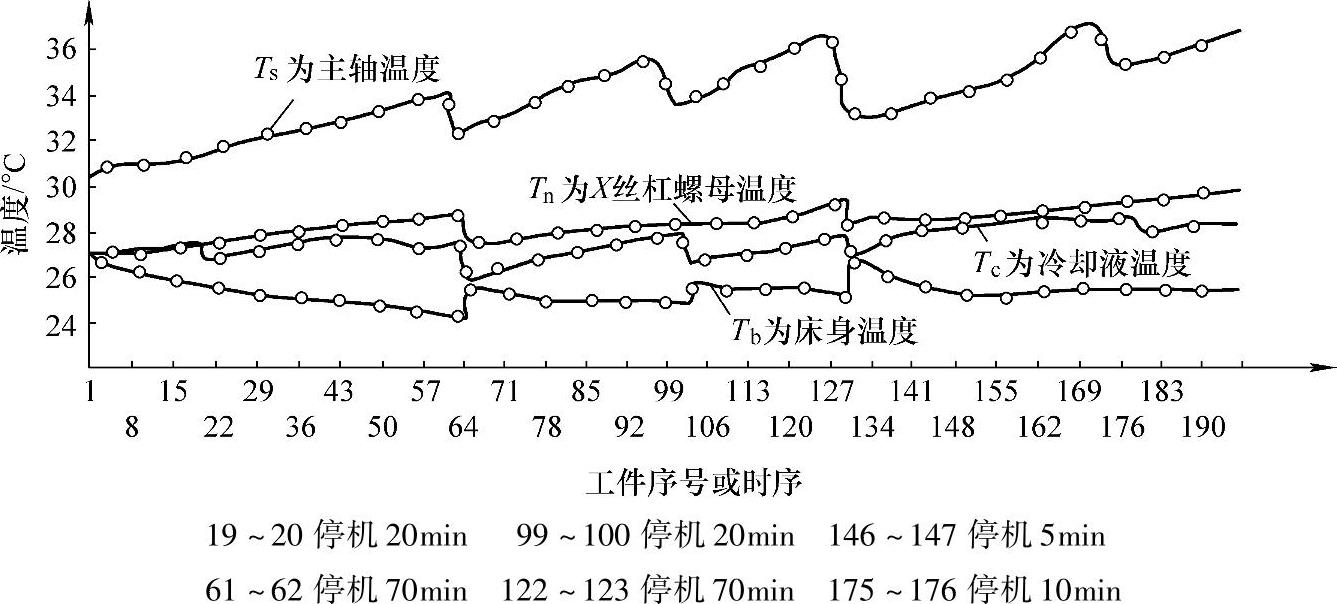
图7-16 机床四个关键点温度变化图

这里的热误差具体是指由于机床温度变化造成机床各部件热变形而产生的刀具与工件之间的相对位置误差，热误差的数值可通过位移传感器测量获得，也可通过直接测量被加工工件的尺寸误差获得。

（2）热误差建模的具体步骤 热误差具体建模步骤如下：

1）选择数学模型形式。为实际应用方便，设热误差是温度的多元线性回归函数，则其回归函数可表示为

Δ_r=a+b₁T_c+b₂T_n+b₃T_s+b₄T_b

式中Δ_r——热误差径向分量；

a——回归常数；

b₁、b2、b3、b4——回归系数。

2）将建模试验数据（每组四个关键点温度值和对应的热误差值）分别代入回归函数并写成矩阵形式：

根据以上方程组可得正规方程组：

3）解正规方程组可得

a=28.2，b₁=-4.2，b₂=-2.7，b₃=-1.5，b₄=7.9

4）将回归常数a及回归系数b₁、b₂、b₃、b₄代入回归函数可得热误差径向分量的数学模型：

Δ_r=28.2-4.2T_c-2.7T_n-1.5T_s+7.9T_b

图7-17所示为机床热误差径向分量变化和用最小二乘拟合法进行建模的分析图。从图7-17中看出，误差模型拟合得较好，残差小于10μm，可满足被加工工件尺寸公差24_μm的精度要求。

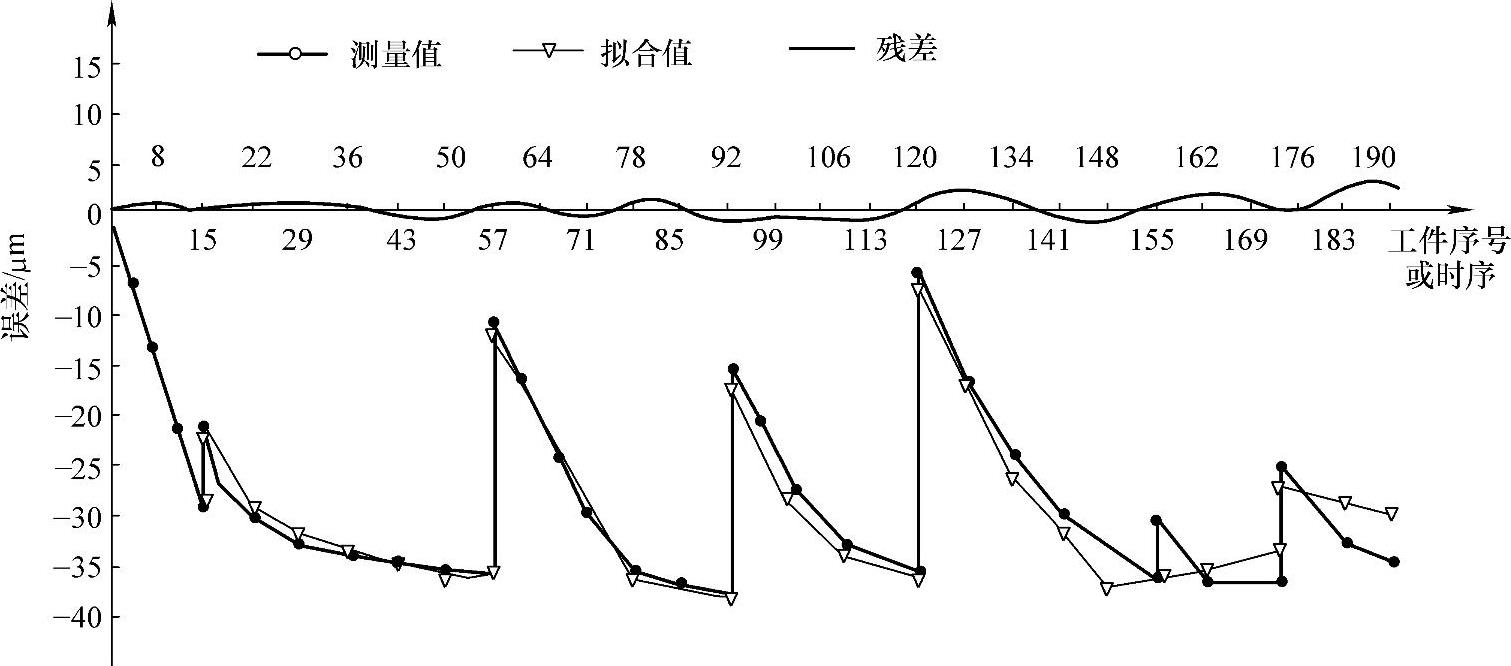
图7-17 机床热误差变化及最小二乘建模分析图

由于机床几何误差占总误差的分量较小（忽略几何误差的影响），由误差综合数学模型：

ΔW_x=δ_xx+δ_xz-η_szz+（ε_βz+ε_βx^-ηrs）T_z-（ε_βz-η_rs）M_ctz+M_rczη_rs+Δ_stx可知综合模型中的热误差元素为Δ_stx，故仅考虑机床热误差元素，误差数学模型可为

ΔW_x=Δ_stx=Δ_r=28.2-4.2T_c-2.7T_n-1.5T_s+7.9T_b