机床几何与热复合误差建模实例分析

图5-9 温度传感器实际布置图

1.机床几何与热复合误差检测及分析

XYTZ型加工中心的X、Y、Z轴行程分别为850mm、560mm、650mm。温度传感器分别布置在X、Y、Z轴的丝杠螺母及导轨上，分别测量X、Y、Z轴丝杠螺母温度及导轨温度。图5-9为温度传感器实际布置图。其中T₁、T₃、T₅分别用于测量机床X、Y、Z轴丝杠螺母温度，T₂、T₄、T₆分别用于测量机床X、Y、Z轴导轨温度。

机床空运行，X、Y、Z轴以一定的进给速度运行，使机床温度不断升高，每隔一段时间测量一次机床温度和机床定位误差，图5-10所示为机床不同检测时间（不同温度）下的定位误差。

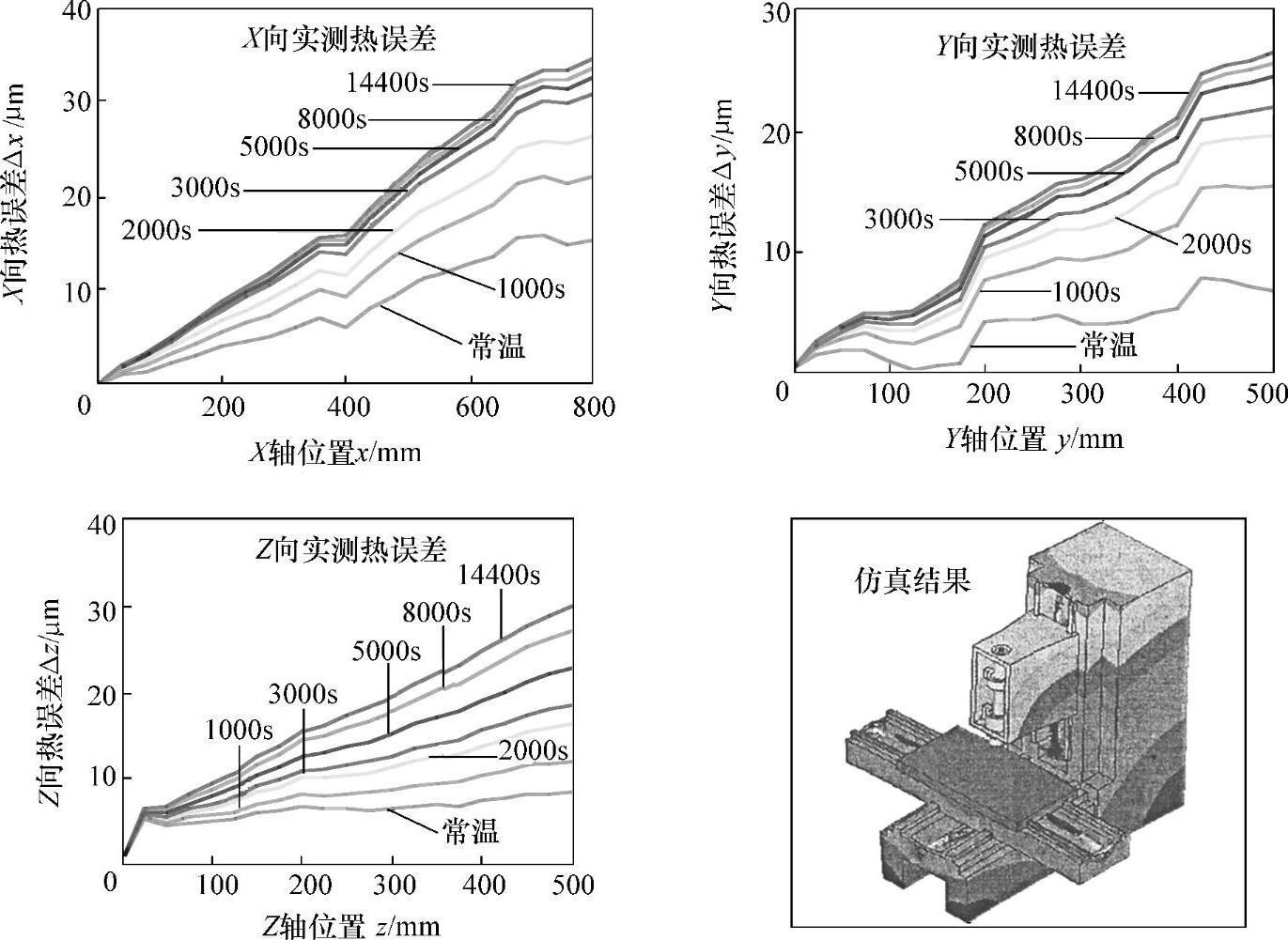
图5-10 机床不同温度下的定位误差

由图5-10可以看出，机床不同温度下的定位误差随着机床温度和坐标位置的增加而增大，而且各条误差曲线的形状基本保持不变，只是各曲线的趋势线斜率随着机床温度在有规律地变化，即机床不同温度下的定位误差是机床原始定位误差绕某一点旋转一定角度。这一规律为机床热误差建模提供理论依据，即机床热误差元素与误差曲线趋势线的斜率有关，同时机床热误差又与机床坐标位置有关。因此，这种复合误差可分离成式（5-4）的形式。

2.几何误差元素建模

由上节分析可知，机床热误差与误差曲线的趋势线斜率和坐标位置有关。以X向热误差为例，几何与热复合误差建模时首先将常温下的几何误差旋转至水平位置（见图5-11），并对旋转后的误差曲线进行建模。

由正交多项式的误差建模方法可得旋转后的几何模型：

δ_ppG（p）=-0.75+0.0163x-0.00013x²+3.04×10^-7x³-2.1×10^-10x⁴

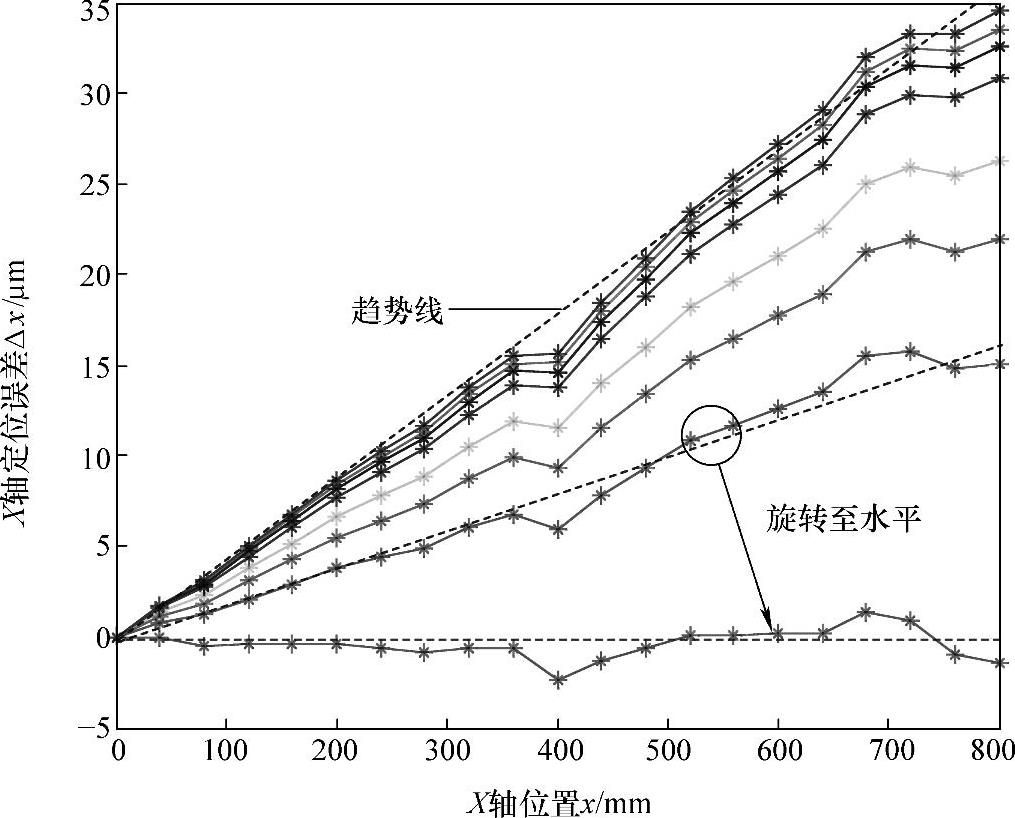
图5-11 机床不同温度下X轴定位误差建模

3.热误差元素建模

对图5-11所示所有误差曲线进行一次线性拟合，可得各测温点的趋势线斜率。根据相关性分析，机床X轴丝杠螺母和X导轨温度对X向热误差影响较大。因此，取这两处测温点的温度进行X向热误差建模。各测量时刻所对应的斜率与温度见表5-5。

表5-5 斜率与温度统计

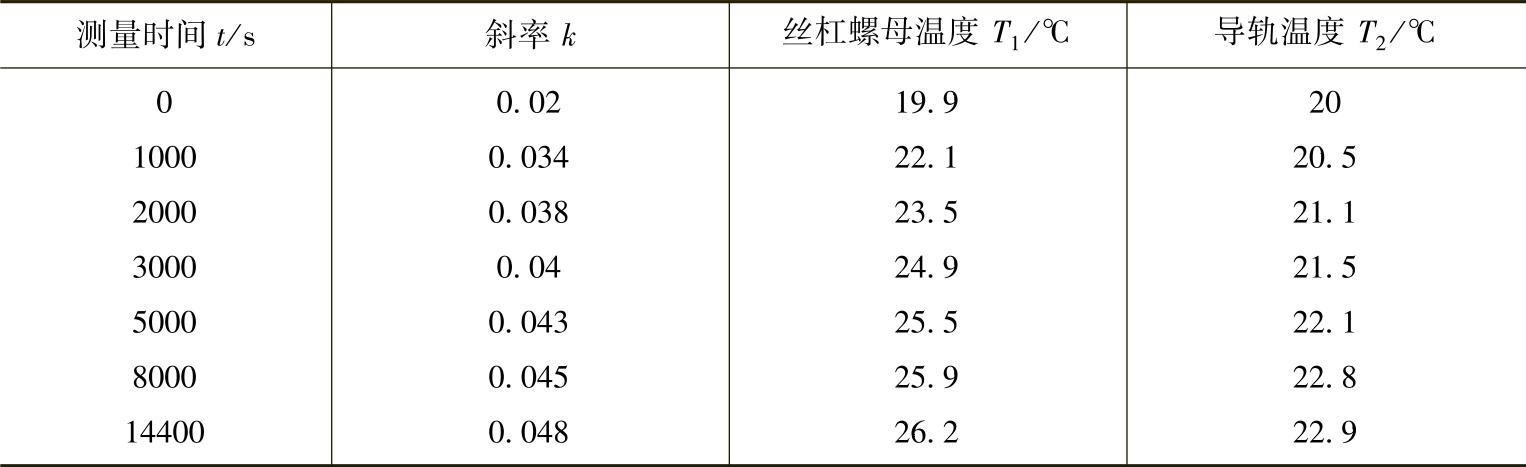
设热误差趋势线斜率δ_ppT（T）是温度T₁、T₂的一次函数，由式（5-4）可得

δ_ppT（T）=b₀+b₁T₁+b₂T₂

将表5-5中的试验数据代入上式，由最小二乘法可得

δ_ppG（T）=-0.0513+0.0042T₁-0.0006T₂(https://www.xing528.com)

由于各误差曲线趋势线过原点，因此可得X向热误差趋势线方程：

δ_ppT（T）·p=（-0.0513+0.0042T₁-0.0006T₂）·x

4.几何与热复合误差建模

将旋转后的几何误差模型及热误差趋势线方程代入式（5-4）可得X向几何与热复合误差模型为

δ_xx（x，T）=-0.75+0.0163x-0.00013x²+3.04×10^-7x³-2.1×

10^-10x⁴+x·（-0.0513+0.0042T₁-0.0006T₂）

图5-12所示为X向几何与热复合误差拟合结果。由图5-12可以看出，几何与热复合误差的拟合残差为[-2～+2μm]，误差拟合精度为95%，拟合精度较高。

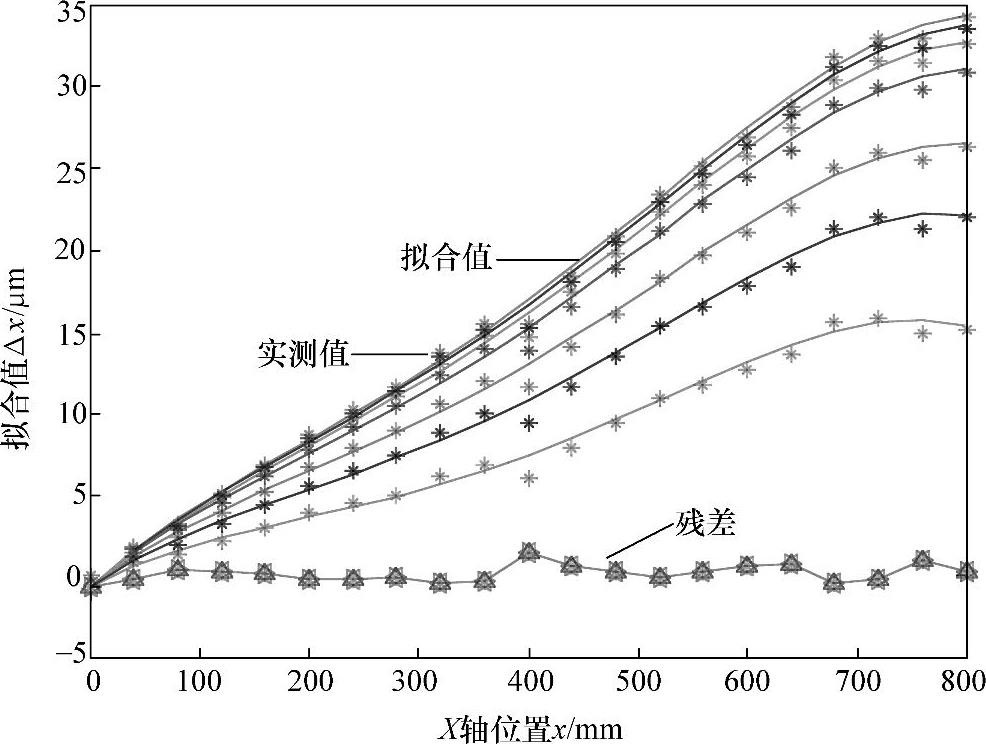
图5-12 机床不同温度下X轴定位误差拟合结果

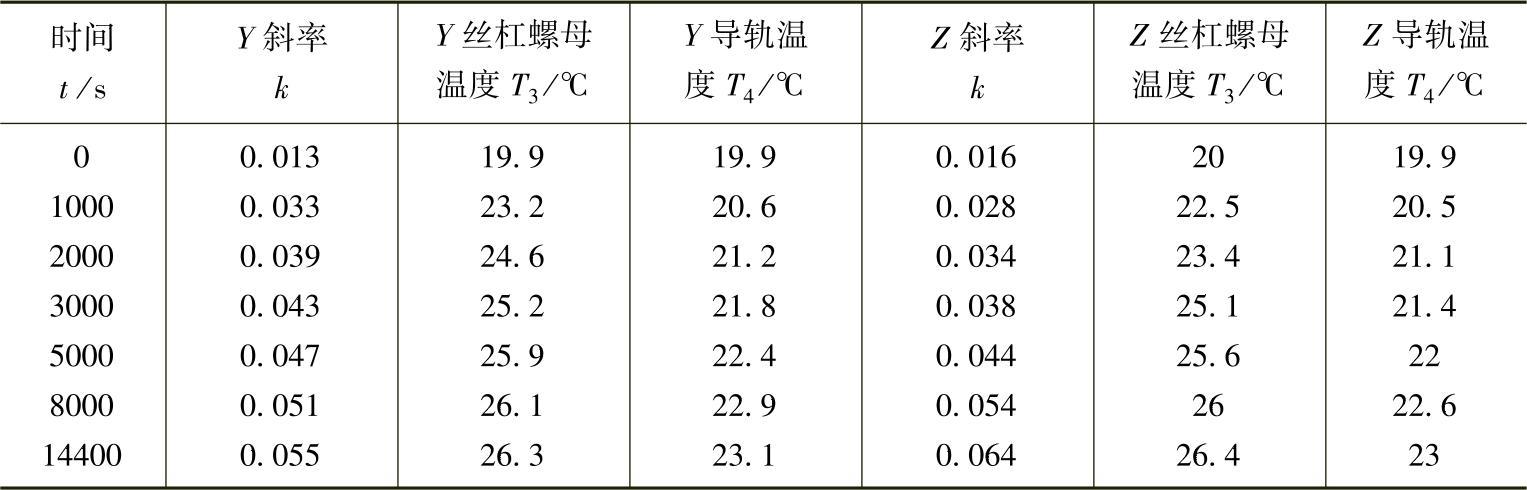
采用同样的建模方法，可以得到Y向和Z向的几何与热复合误差模型。Y、Z向热误差趋势线斜率和温度统计结果见表5-6。

表5-6 Y、Z向斜率与温度统计结果

采用同样的建模方法可得Y、Z向的几何与热复合误差模型为

δ_yy（y，T）=-0.31-0.0008y+（-0.1392+0.0049T₃+0.0028T₄）·y

δ_zz（z，T）=1.28+0.051z-4.1×10^-4z²+10^-6z³-8.09×10^-10z⁴+（-0.273+0.0001T₅+0.0145T₆）·z

图5-13所示为Y向几何与热复合误差拟合结果。由图5-13可以看出，Y向拟合残差为-3～+1μm，拟合精度为94%，误差拟合精度较高。

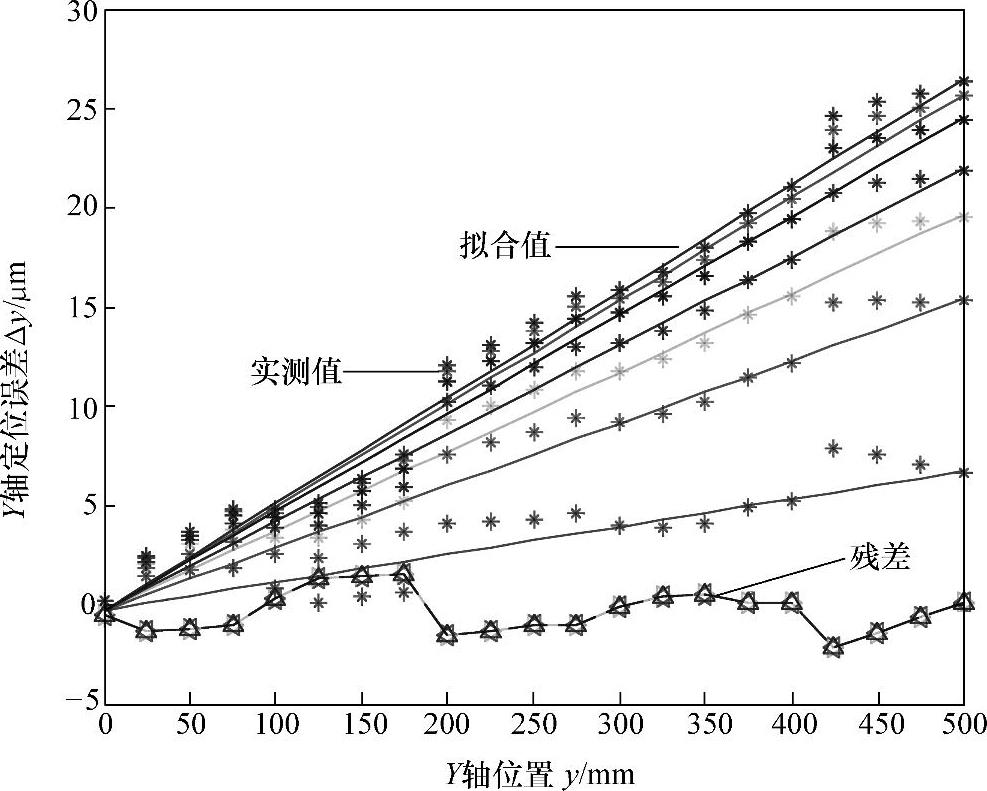
图5-13 不同温度下Y轴定位误差拟合结果

图5-14为Z向几何与热复合误差拟合结果。由图5-14可以看出，Z向拟合残差为-2～+1μm；Z向的拟合精度为97%，误差拟合精度较高。

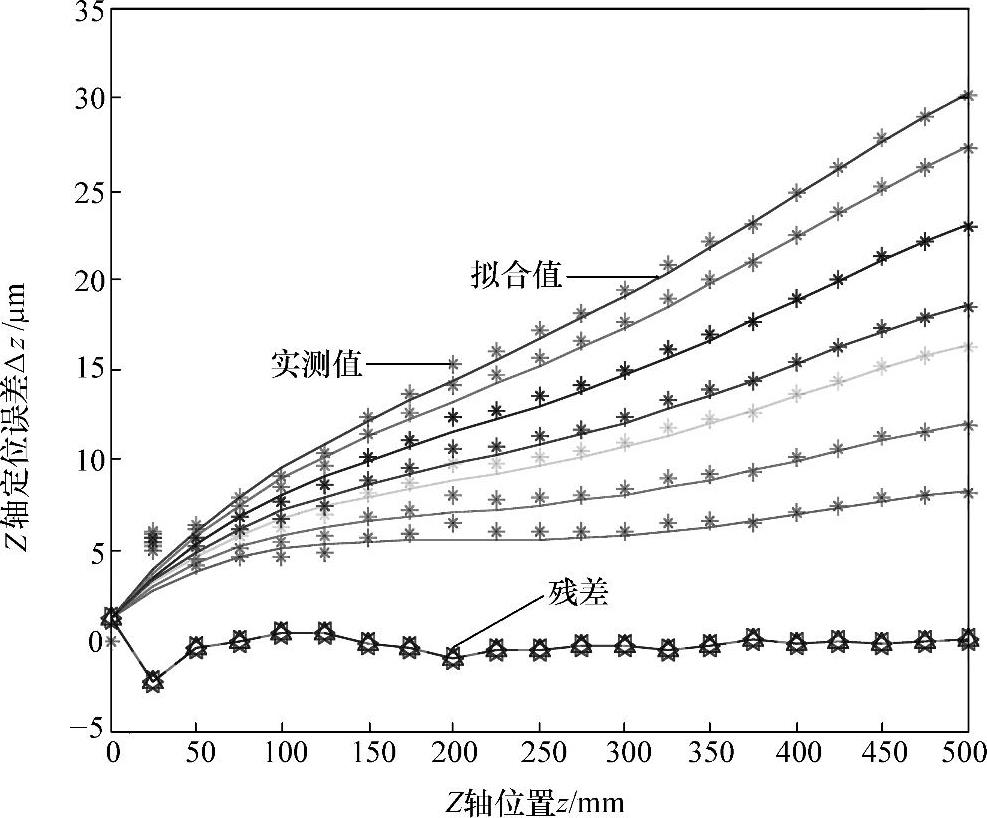
图5-14 不同温度下Z轴定位误差拟合结果