1.误差检测及分析
根据机床几何误差检测原理，对一台XYTZ型加工中心进行三个移动轴X、Y、Z的几何误差检测，其几何误差元素测量结果数据见表5-1。
表5-1 XYTZ型加工中心的几何误差测量结果数据
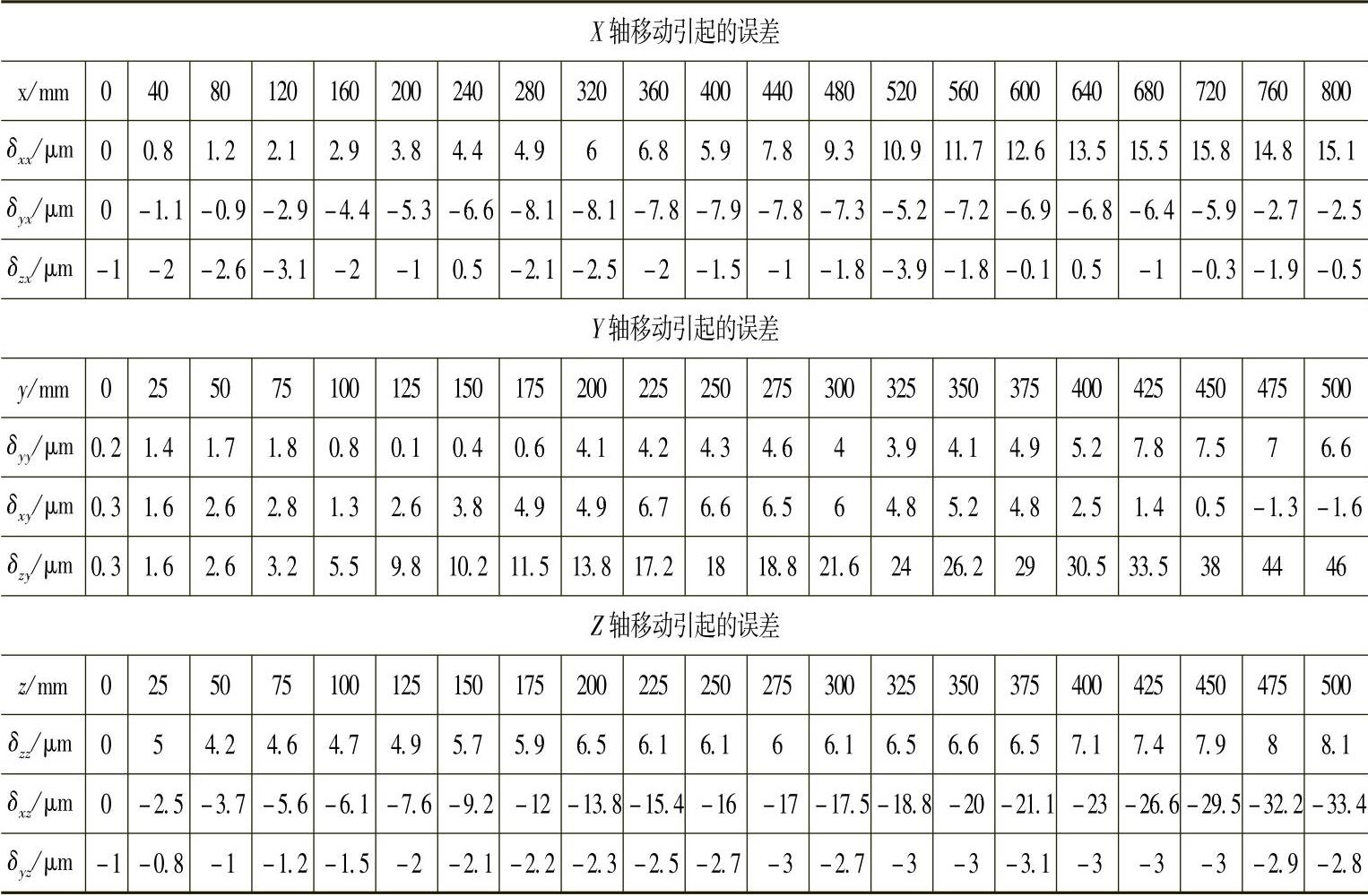
图5-1所示为几何误差曲线分布图，由机床几何误差元素分布图可知，X轴的线性位移误差δxx偏离原点正方向最大，达到+16μm，而且整个误差走向趋势和坐标轴位置基本呈线性关系；其次是Y向直线度误差δyx偏离原点负方向最大，达到-8μm，误差走向和坐标轴位置呈非线性关系；而Z向直线度误差δzx则较小，在-4～+1μm之间做窄幅振荡，误差走向与坐标轴位置基本呈线性关系。
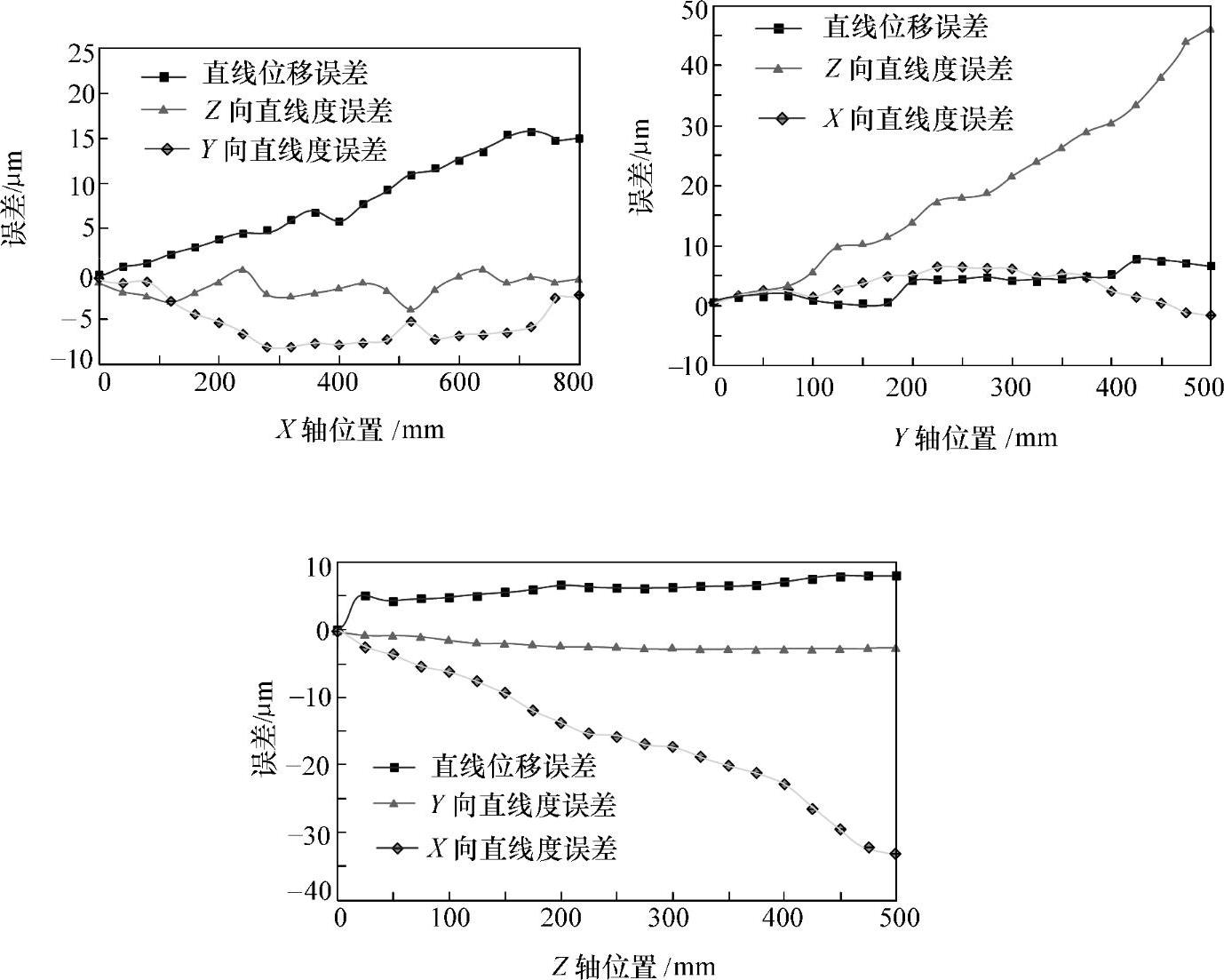
图5-1 几何误差曲线分布图
Y轴的Z向直线度误差δzy偏离原点正方向最大，达到+46μm，而且整个误差走向趋势和坐标的位置基本呈线性关系；其次是线性位移误差δyy比较大，最大为+8μm，误差走向趋势和坐标的位置呈非线性关系；而X向直线度误差δxy最小，达到+7μm，整个误差走向趋势和坐标的位置呈非线性关系。
Z轴的X向直线度误差δxz偏离原点负方向最大，达到-34μm，而且整个误差走向趋势和坐标的位置呈非线性关系；其次是线性位移误差δzz比较大，为+8μm，误差走向趋势和坐标的位置基本呈线性关系；而Y向直线度误差δyz最小，在-3～+1μm之间窄幅振荡，整个误差走向趋势和坐标的位置呈明显的线性关系。
2.建模过程
由于基于最小二乘法的回归建模方法研究较为成熟，这里采用正交多项式法进行建模。根据试验数据选择相应的正交多项式表，根据每组测量误差元素有21个试验数据，选择N=21的正交多项式表见表5-2。表5-2中左上部分及Si摘自正交多项式表，ϕi为正交函数族，Bi=∑ϕi（xi）δi，pi=βiBi。下面以X轴定位误差δxx为例具体说明正交多项式建模方法。
1）将实测数据δxx按顺序放入δxx列，并计算出相应数据的平方按顺序放入δ2xx列，见表5-2。
2）进行计算，分别将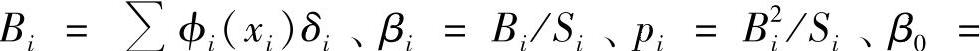
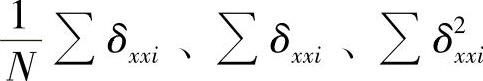的计算结果放入表5-2的相应位置。
表5-2 一元正交多项式计算表
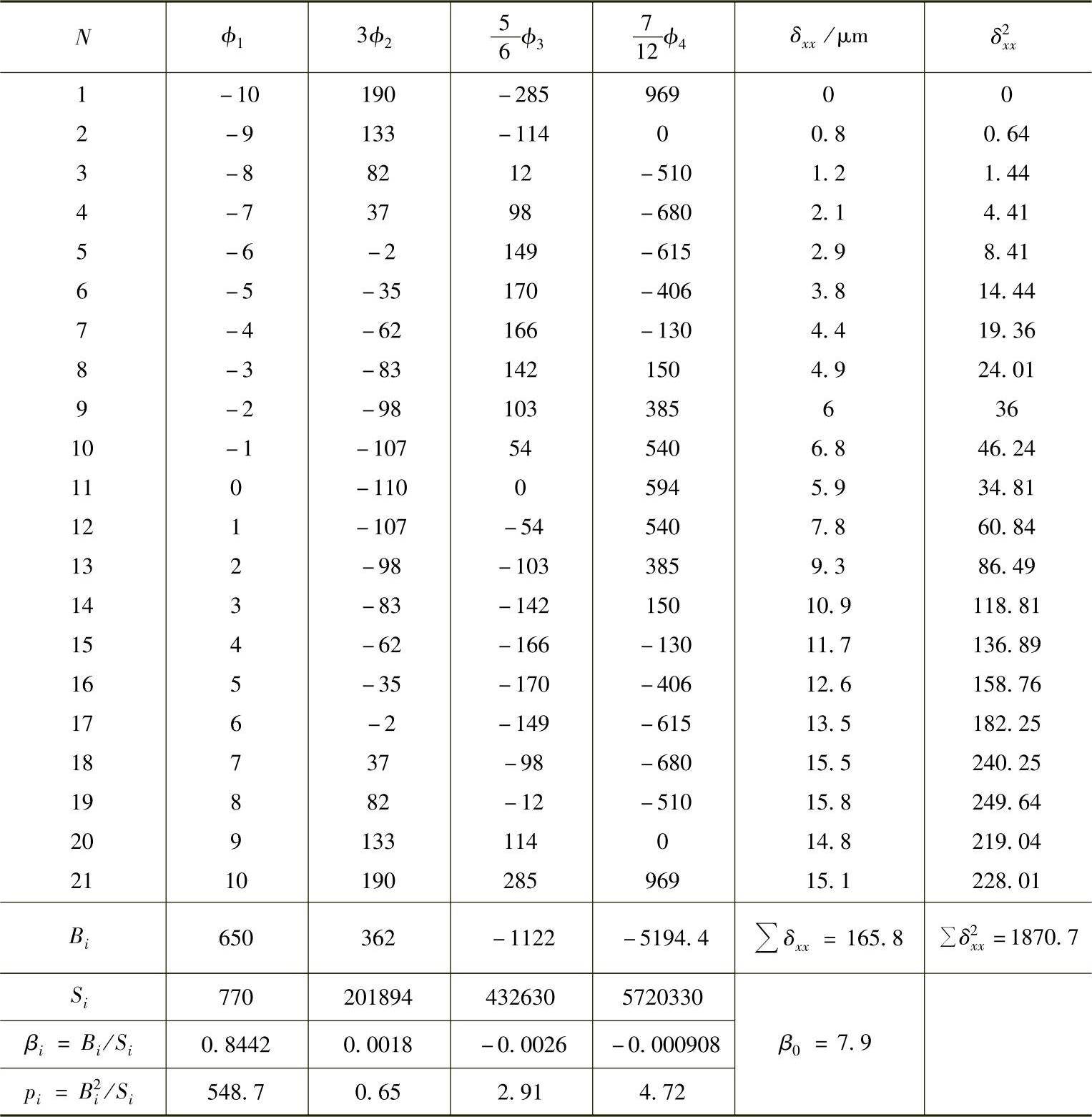
3）计算总偏差：
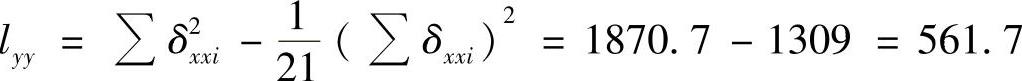
4）作方差分析表，见表5-3。
表5-3 正交多项式方差分析表
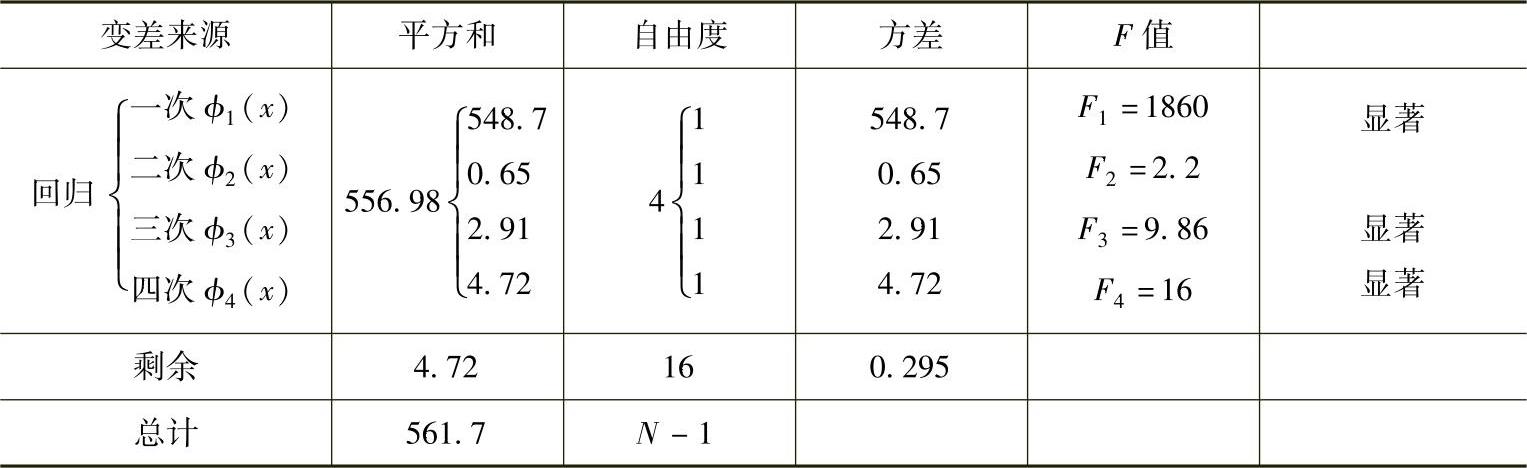
5）F检验。对于F0.1（1，16）=3.05、F0.05（1，16）=4.49、F0.01（1，16）=8.53，由表5-3可知一次项、三次项和四次项显著，因此建立如下回归方程：
δxx=7.9+0.8442ϕ1（x）-0.0026×5ϕ3（x）/6-0.000908×7ϕ4（x）/12
6）正交函数回代。(www.xing528.com)
由正交函数族：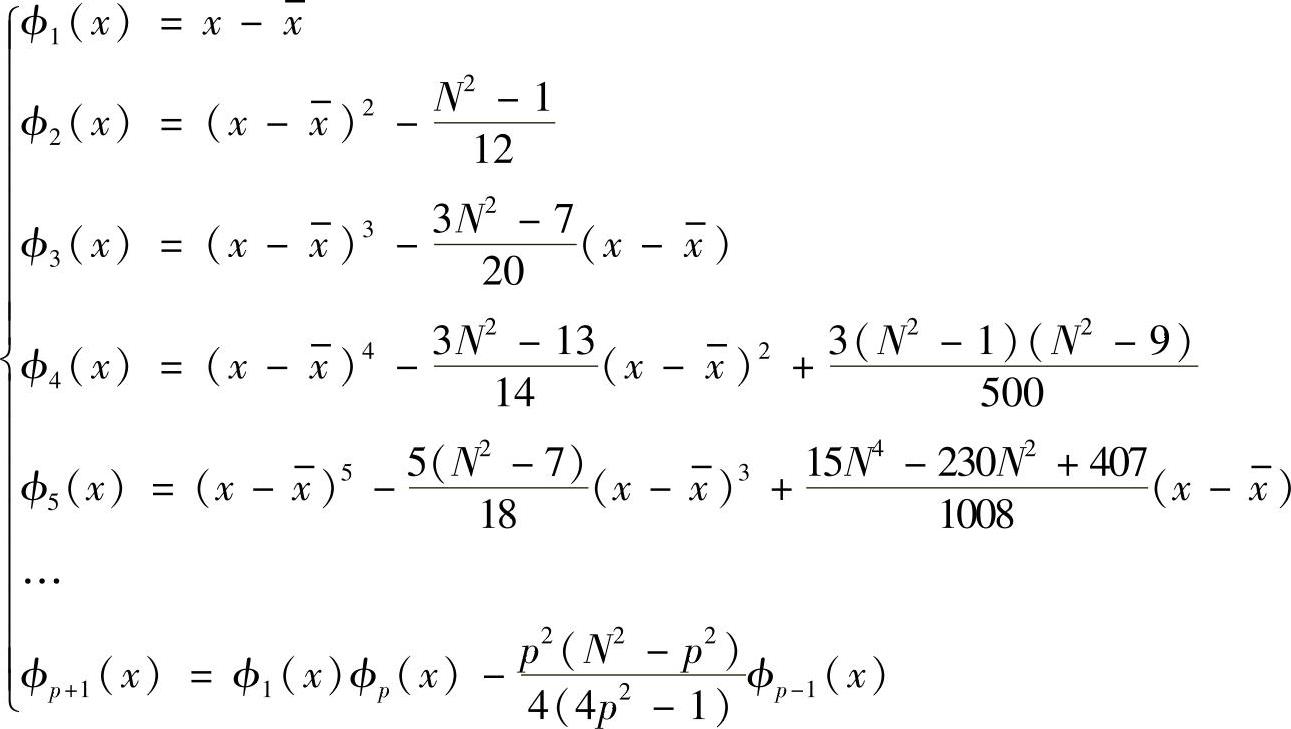
将ϕ1（x）、ϕ3（x）、ϕ4（x）代入第五步的回归方程整理得
δxx=7.9+0.8442（x-11）-0.0026×[（x-11）3-65.8（x-11）]×
5/6-0.000908×[（x-11）4-95.57（x-11）2+1140.5]×7/12
7）函数变换。由于正交函数族中的变量为自然数，因此作函数变换x=（X+40）/40，其中X为X轴的位置坐标，将变换函数代入第六步回归方程得X轴移动时的线性位移误差模型：
δxx=-0.75+0.037x-0.00013x2+3.04×10-7x3-2.1×10-10x4
同理，可得X轴移动时的Y向直线度误差模型和Z向直线度误差模型：
图5-2所示为X轴移动时线性位移误差δxx、Y向直线度误差δyx和Z向直线度δzx的拟合结果及拟合残差，可见，拟合精度为[-3～+3μm]，故建模精度较高。
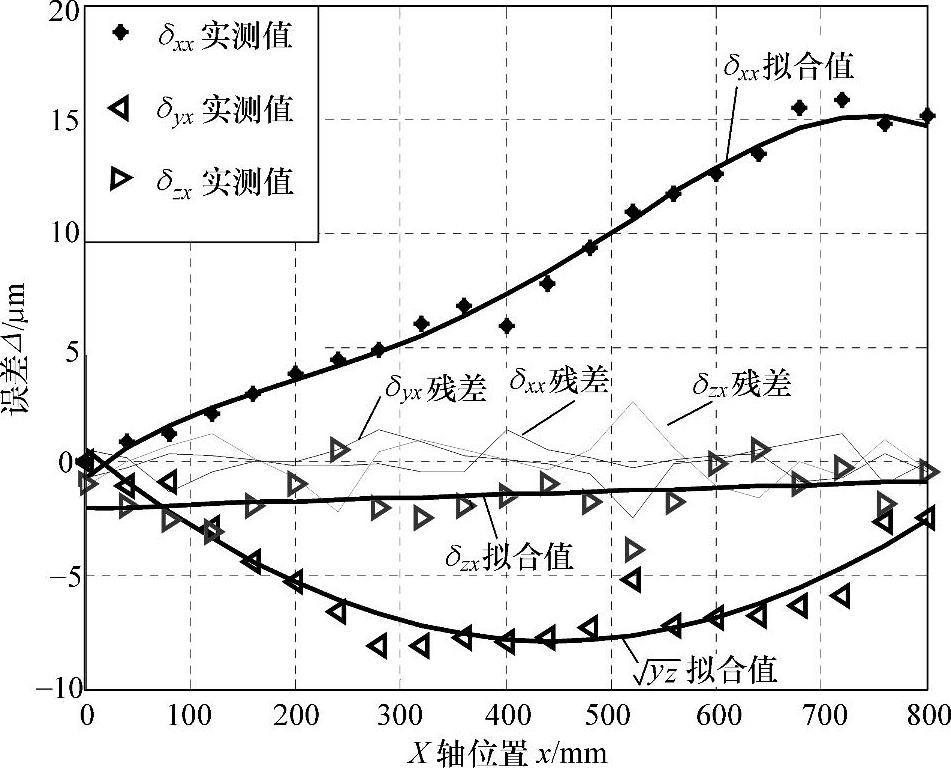
图5-2 X轴几何误差拟合结果
采用同样的建模方法，可得Y轴移动时的线性位移误差δyy、X向直线度误差δxy、Z向直线度误差δzy的数学模型：
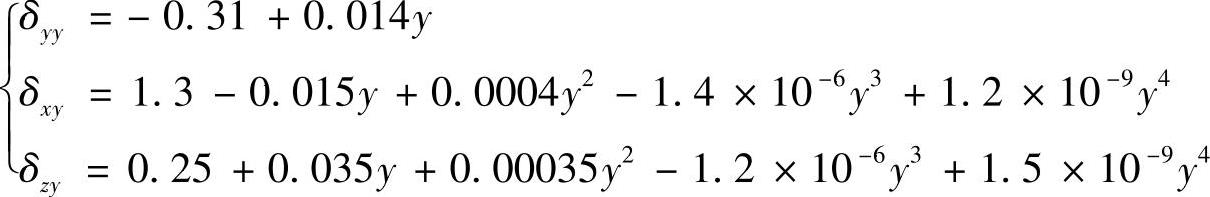
图5-3所示为Y轴移动时几何误差的拟合结果及拟合残差。
同理，可得Z轴移动时的线性位移误差δzz、X向直线度误差δxz、Y向直线度误差δyz的数学模型：
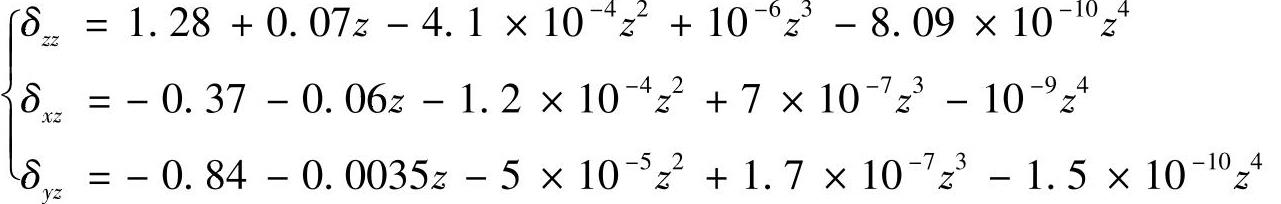
图5-4所示为Z轴移动时几何误差的拟合结果及拟合残差。
由图5-3及图5-4可以看出，基于正交多项式的几何误差建模精度较高，Y向建模残差为-1.5～+2μm，Z向建模残差为-1～+1.5μm。
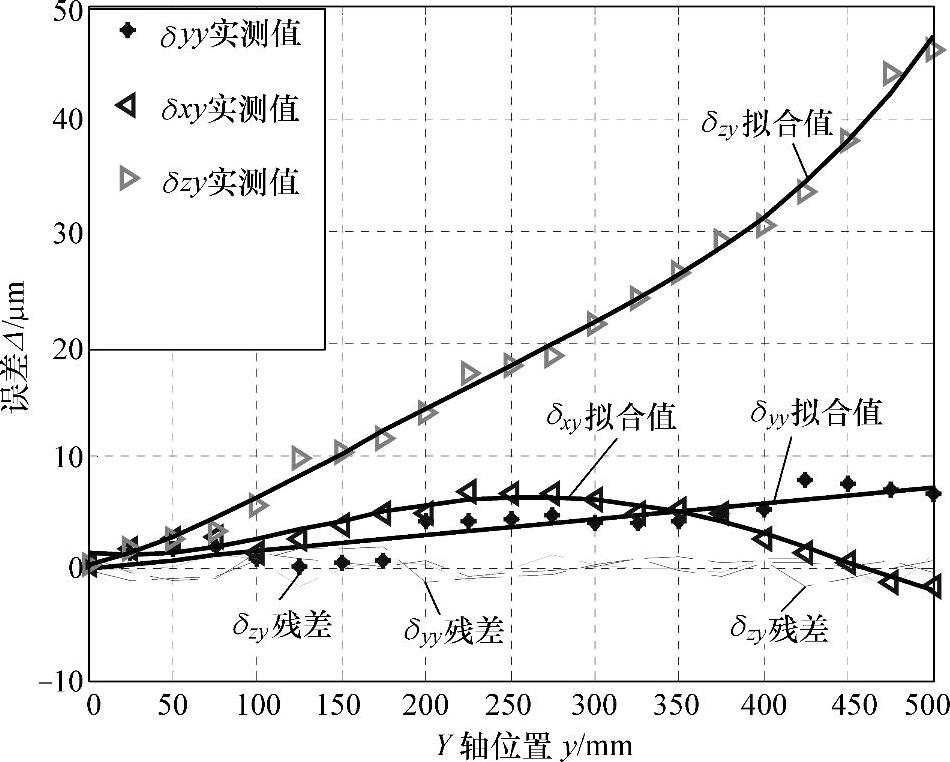
图5-3 Y轴几何误差拟合结果
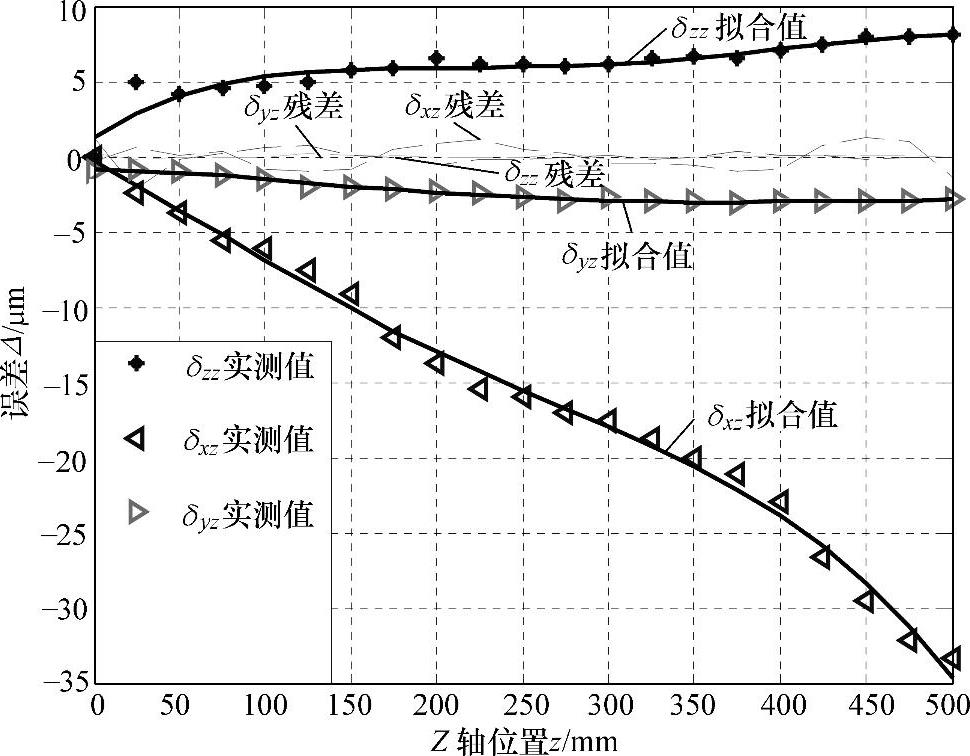
图5-4 Z轴几何误差拟合结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
