温度测点布置技术优化方案

1.温度测点的选择

在机床热误差的补偿中，温度测点的布置是关键和难点。选择适当的温度测点不但能减少用于建模的测点数目，简化建模过程和热误差模型，而且还可提高机床热误差模型的精度。

在几乎所有应用的热误差补偿系统中，温度测点位置的确定在一定程度上是根据经验进行试凑的过程，称为试凑法。它通常是先基于工程判断，在机床的不同位置安装大量的温度传感器，再采用统计相关分析来选出少量的温度传感器用于误差元素的建模。具体步骤如图4-36所示。

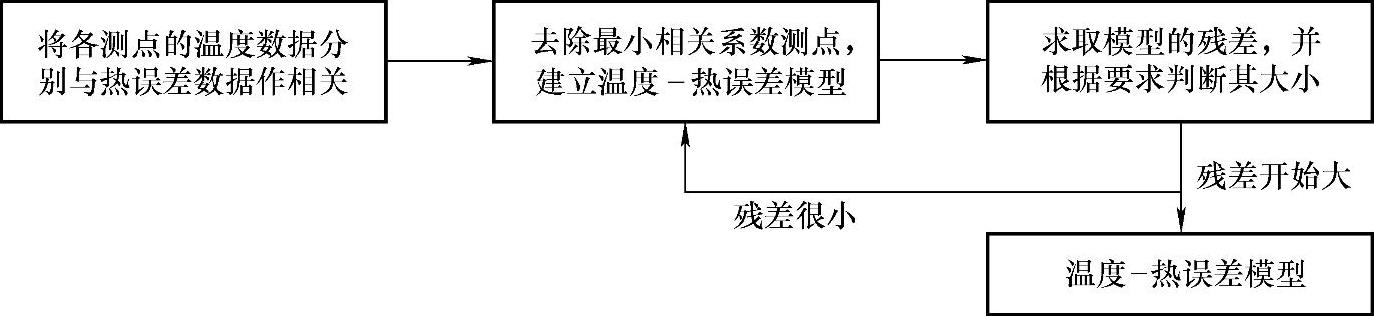
图4-36 试凑的具体步骤

2.温度测点布置策略

（1）主因素策略 主因素策略的意思是用于热误差建模的各温度测点数据T_ij应与热误差数据E_j有一定的联系，即具有一定的相关性，用数学式子表达为

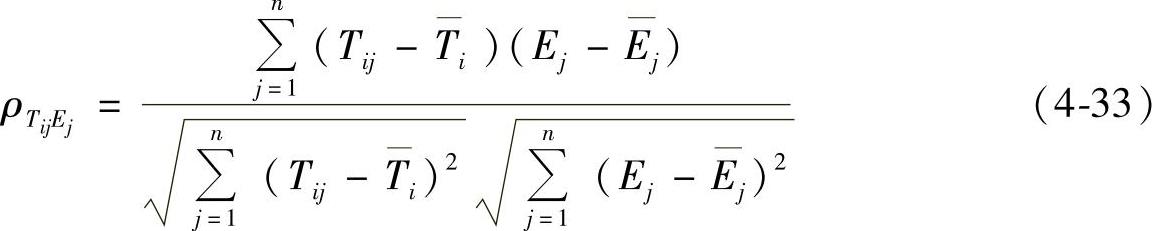
式中i=1，2，…，m，m——温度测点数；

j=1，2，…，n，n——测量数据个数。

根据具体情况选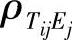取，如可取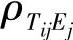>0.8的误差元素为主因素。

（2）能观测性策略 能观测性策略是指所选温度点的温度信号能否具有一定精度地表达机床热误差。

对于机床热动态过程，一般有

T=AT+BQ

ΔＬ=CT+DQ

式中T——机床温度矩阵；

ΔＬ——热误差（输出）矩阵；

Q——热源（输入）矩阵；

A、B、C、D——常数矩阵。

状态完全能观测（即温度T能表达热误差ΔＬ）的充分必要条件是其能观测性矩阵：

G=[C^TA^TC^T…（A^T）^n-1C^T]满秩。由此可得下列结论：

1）可观测性条件或温度对于热误差的表达与温度传感器在机床上的位置紧密相关。

2）只要布置合适，少量的温度测点也能表达热误差。

3）为了保证可观测性或用温度表达热误差，温度传感器应避免布置在特征函数的零点位置上。

（3）互不相关策略 根据主因素准则获取了一定数量的与热误差有关温度测点。但这些温度测点之间有的具有相关性，可互相表达。另外，若把这些温度测点全部用于建模，由于温度测点之间相关而造成互相影响使热误差估计精度下降。故应聚类选取，即从每一相关类中选出一个作为代表用于热误差建模。这样既可减少用于热误差建模的温度传感器数量，又可提高建模精度。可使用模糊理论进行温度测点的聚类选取。

（4）最少布点策略 在满足机床加工精度的条件下，若能用最少的温度测点来估计热误差，所带来的好处是显而易见的。在满足主因素、互不相关条件及机床加工精度的条件下，放宽残差限度，逐步在建模中减少温度测点，搜索最佳测点组合，使用于热误差建模的温度传感器测点数减少到最低限度。

（5）最大灵敏度策略 机床上各点的温度变化对机床热误差的影响程度不同，有些点的温度变化将引起机床热误差的明显变化，这些点就为热误差敏感点。热误差敏感点应为机床热误差补偿中所考虑的温度测点。具体选择过程：首先建立各温度测点的温度变化与热误差（可为位移测点的位移）变化之间的关系，然后根据这种关系所确定的导数关系辨识各温度测点的温度变化对热误差的影响程度，影响程度大的测温点即为热误差敏感点，作为用于热误差建模的候选点。用数学式表达为

式中ΔR_T——机床热误差；

T_i——各温度测点的温度；

ρ_m——热误差敏感基数，根据实际情况确定，偏导数大于ρ_m的温度测

点作为用于热误差建模的考虑对象。

（6）最近线性策略 如果能够把温度传感器安置在一些策略的位置，线性模型可用于热误差分析。线性热误差模型与传统的非线性多元回归模型相比，具有训练速度快和更好的外插性能。在满足机床加工精度的条件下，在热误差建模中采用线性模型，搜索最佳测点组合，使得建立出来的热误差模型不但线性而且具有一定的精度。

需要指出的是，以上六个策略互相之间是有联系和影响的，有些仅是考虑的角度不同。例如，在满足了主因素、可观测性条件后，温度传感器应安置在对热误差最敏感，且受其他温度测点干扰最小的位置。但要同时满足这两个要求一般难以达到，有时为了获得测点温度间最小的相关性不得不放弃对热误差的灵敏性。所以，在机床关键温度点的具体选择过程中还要根据实际情况和条件进行综合、全面地考虑。

3.温度测点优化布置

在最终的热误差建模中试凑法将导致大量的时间和传感器的浪费，因为这些浪费的传感器并不用在最终的温度-热误差模型中。

在理论上进行优化布点研究，确定适当的温度测点，不但能减少用于建模的测点数目，简化建模过程和热误差模型，而且还可提高机床热误差模型的精度。

考虑这样一个基本假设：如果能够找到热误差与所选温度场测量数据之间的线性或接近线性的关系，则热特性辨识时间将由于线性预测模型所具有的良好内插和外插性能而大大减少。由此要分析和回答的实际问题之一是是否在热误差与所选温度场测量数据之间存在线性或近似线性关系？如果对该问题的回答为是，则问题之二是这种线性关系在什么条件下存在？其在不同的条件下是否具有鲁棒性？这里根据解析法和有限差分法，使用Matlab软件进行仿真，分析主轴在不同的受热情况下的温度测点优化布置问题，并对以上两个问题给予解答。

（1）主轴一维最佳温度测点布置优化 图4-37所示机床主轴一维简化模型。假设只有左端单一热源。热量从左端输入，从右端传出。同时，轴与周围环境有对流和辐射换热。主轴各点温度变化和由此产生的热伸长为

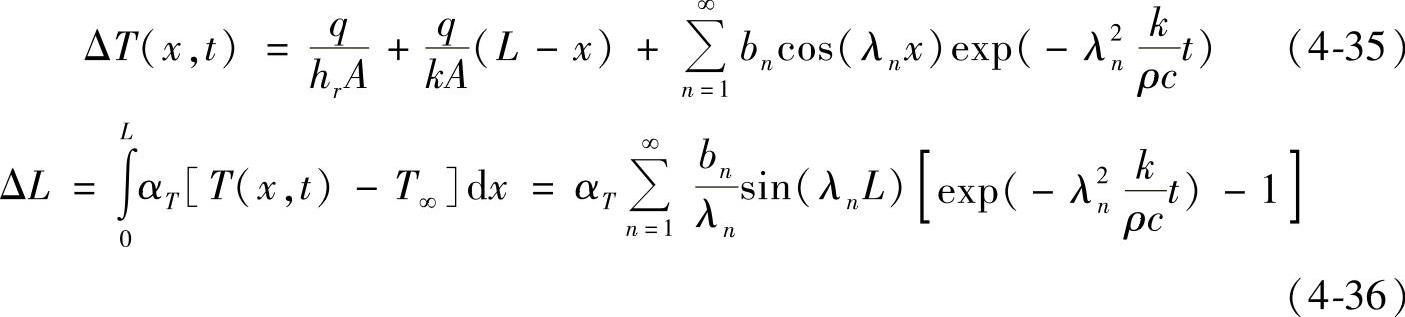
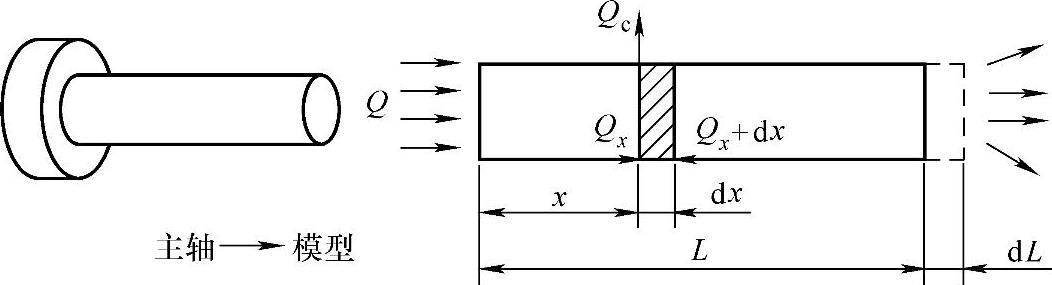
图4-37 机床主轴一维简化模型

在机床热误差补偿中，温度测点的布置是关键和难点，其影响着热误差建模的正确性和补偿的有效性。在几乎所有应用的热误差补偿系统中，温度测点位置的确定是根据经验进行试凑的过程。它通常是先基于工程判断，在机床的不同位置安装大量的温度传感器，再采用统计相关分析来选出少量的温度传感器用于误差元素的建模。试凑法导致大量的时间和传感器的浪费，因为这些浪费的传感器并不用在最终的热误差建模中。在理论上进行优化布点研究，确定适当的温度测点，不但能减少用于建模的测点数目，简化建模过程和热误差模型，而且还可提高机床热误差模型精度。

1）理论分析如下：

导热微分方程：

初始条件：T（x，0）=T∞

边界条件：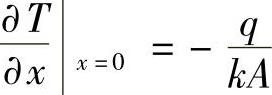

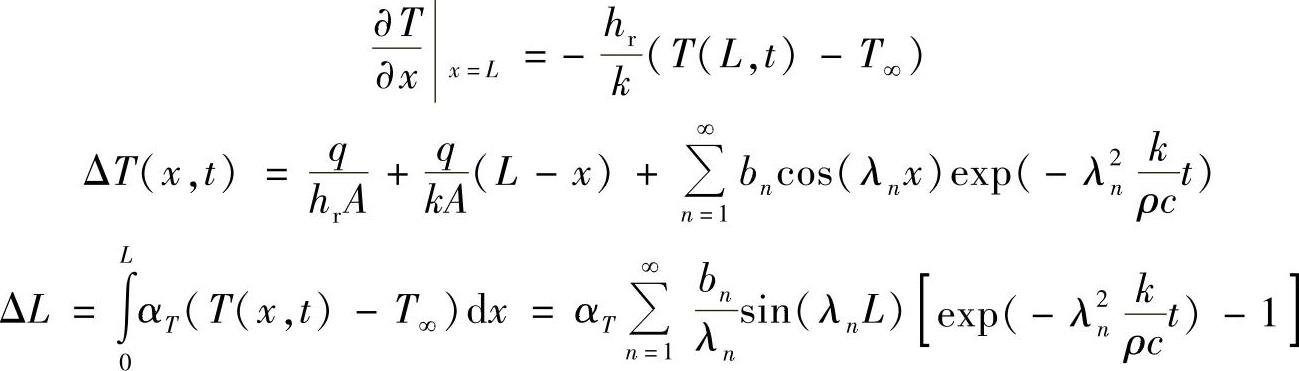(www.xing528.com)

各式中ρ——密度；

c——比热容；

q——热流密度；

k——导热系数；

A——主轴截面积；

h_r——主轴右端单位面积对流换热系数；

L——主轴长度。

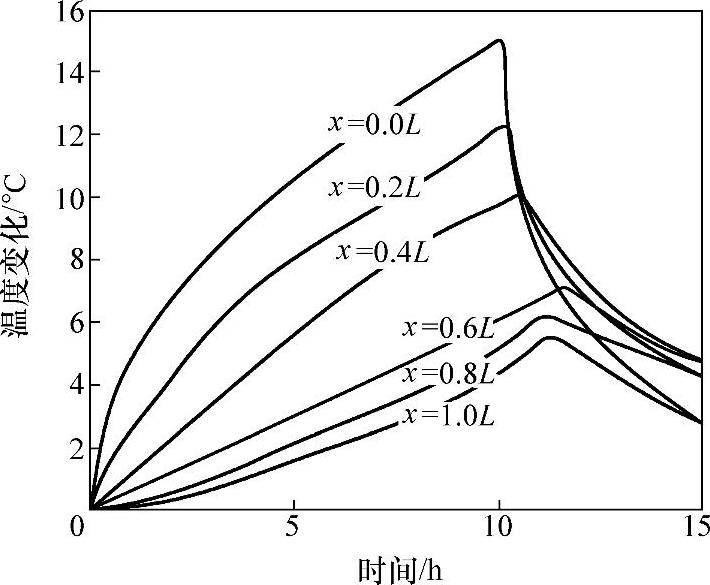
图4-38 主轴单端热源时的温度场

2）主轴温度场与主轴热膨胀。图4-38所示为主轴单端热源时的温度场。由图4-38可知，主轴的温度变化与时间成正比，与位置成反比；远离热源的位置温变小，当温变达到最高后逐渐趋于热平衡状态。

图4-39所示为不同热流密度各位置上ΔT与ΔL关系图。由图4-39可知，主轴热膨胀与热流密度成正比；在机床主轴未达到热平衡前，主轴热膨胀与温变成正比，与位置无关；当主轴达到热平衡后，主轴热膨胀也趋于平衡。

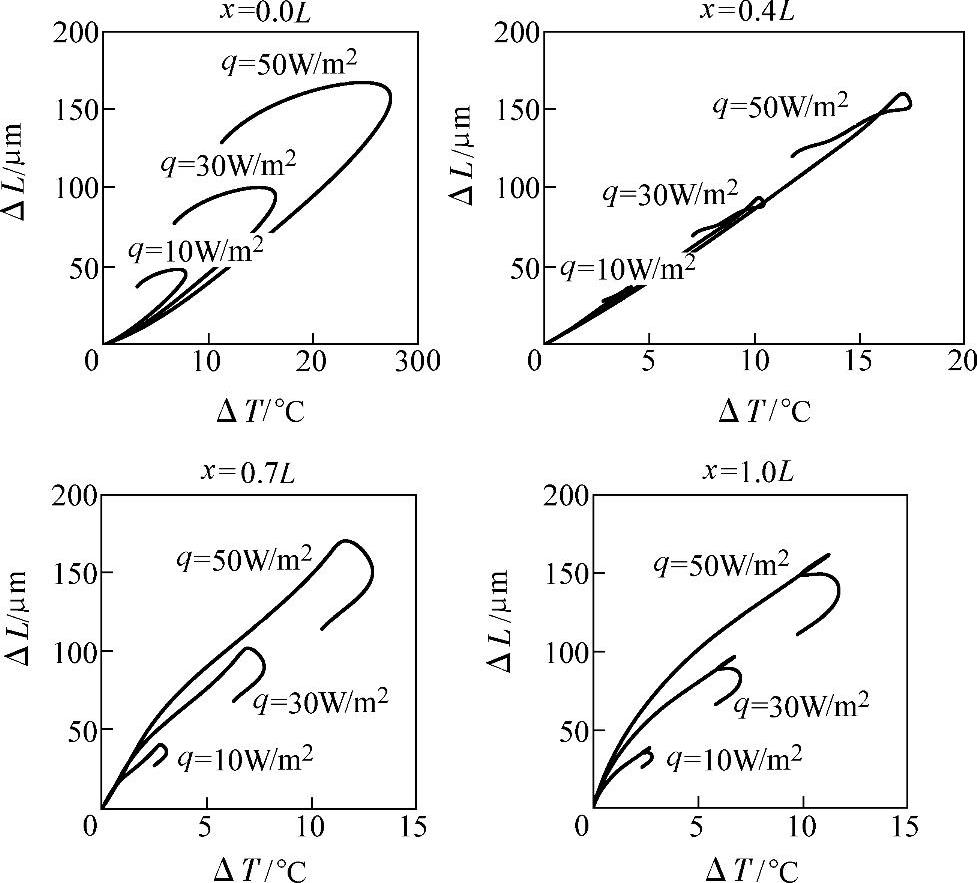
图4-39 不同热流密度各位置ΔT与ΔL关系图

图4-40所示为不同对流放热系数各位置上ΔT与ΔL关系图。由图4-40可知，主轴热膨胀与放热系数成反比，理论上，主轴放热系数越大，主轴热交换越快，主轴的温变小。

图4-41所示为不同热流密度各位置上ΔT和ΔL间关系图。由图4-41可以看出，在大约x=0.40L处，ΔL和ΔT之间具有近似线性关系，并且这一关系具有很强的鲁棒性，基本不受热流密度q变化的影响（这一点也可以从ΔL和ΔT表达式得出），而且受对流换热系数h变化的影响很小。其余位置上的温度变化ΔT和ΔL之间关系线性度很差，受热流密度q和对流换热系数h变化的影响也很大。

3）结论。对于主轴单热源受热情况，在大约x=0.40L处，主轴热误差ΔL和温度变化ΔT之间呈近似的线性关系，并且此关系具有很强的鲁棒性（即受可控参数q和h的变化影响很小），因此0.4L处是最佳温度测点位置。

（2）最佳温度测点的试验分析 图4-42所示为温度测点试验分析示意图。共布置六个温度传感器和一个位移传感器。热源从一端源源不断的传入试件，实时记录各温度传感器及位移传感器的检测结果。

图4-43所示为各测量点的温度变化过程。由图4-43可知，温度变化与测点位置成反比。在达到热平衡前，温变与时间成正比，当温变达到最高后逐渐趋于热平衡。

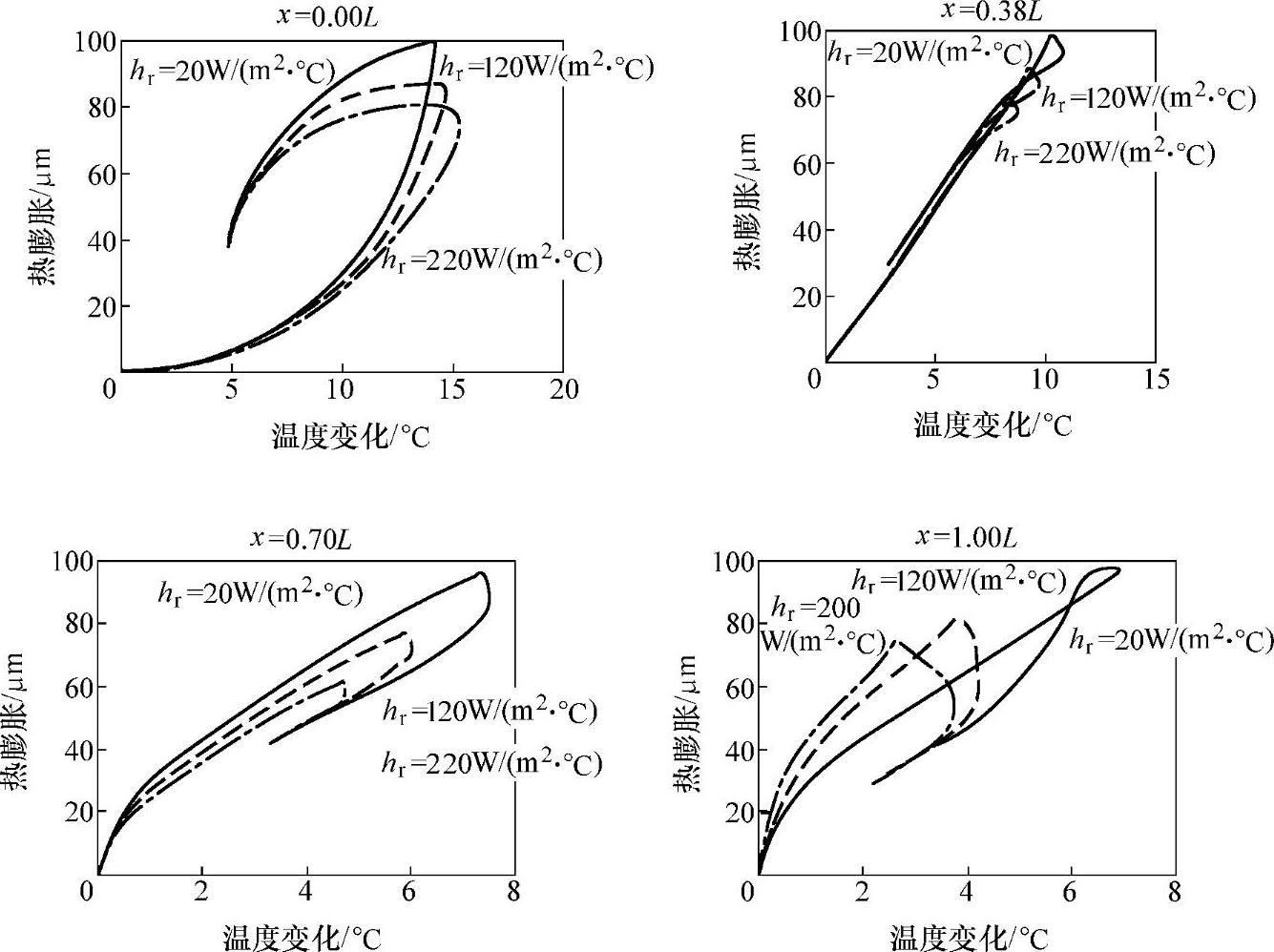
图4-40 不同对流放热系数各位置上ΔT和ΔL间关系图

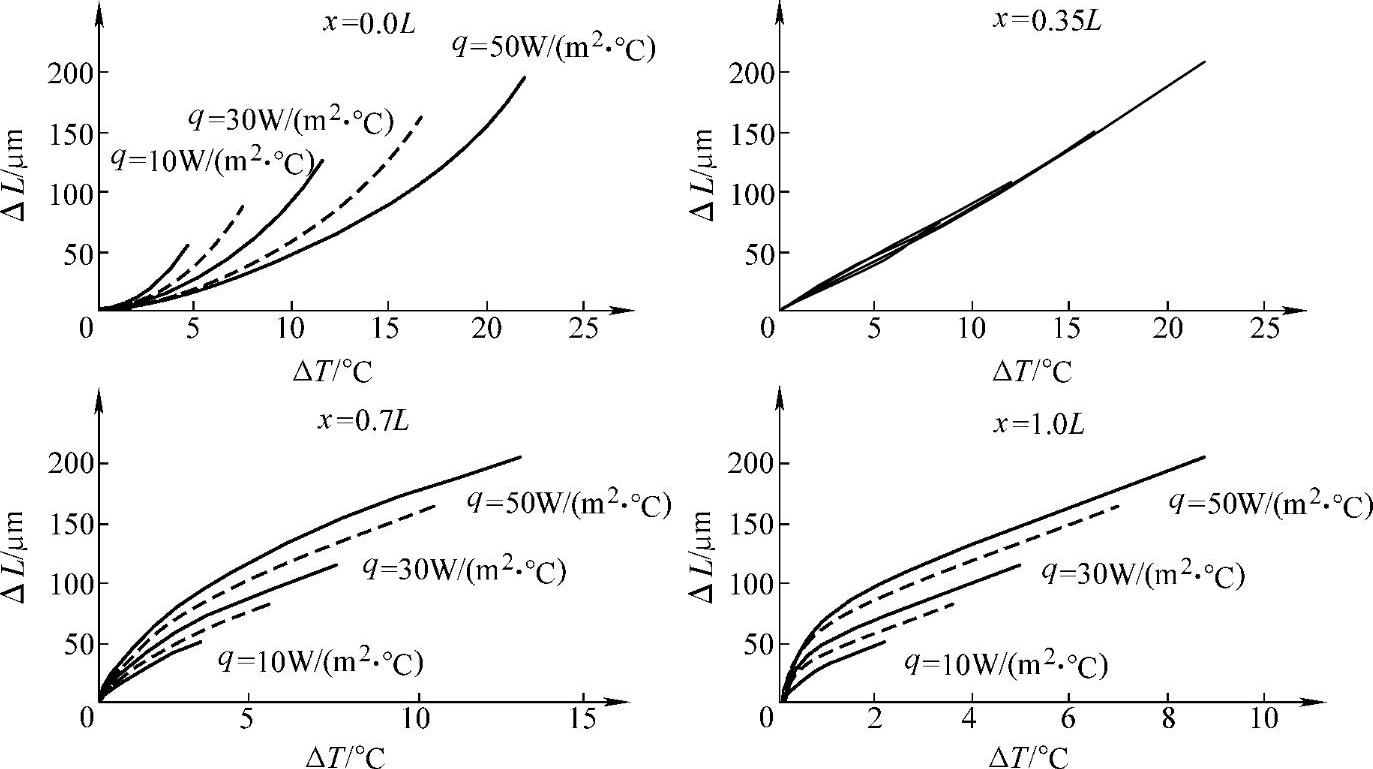
图4-41 不同热流密度各位置上ΔT和ΔL间关系图

图4-42 温度测点试验分析示意图

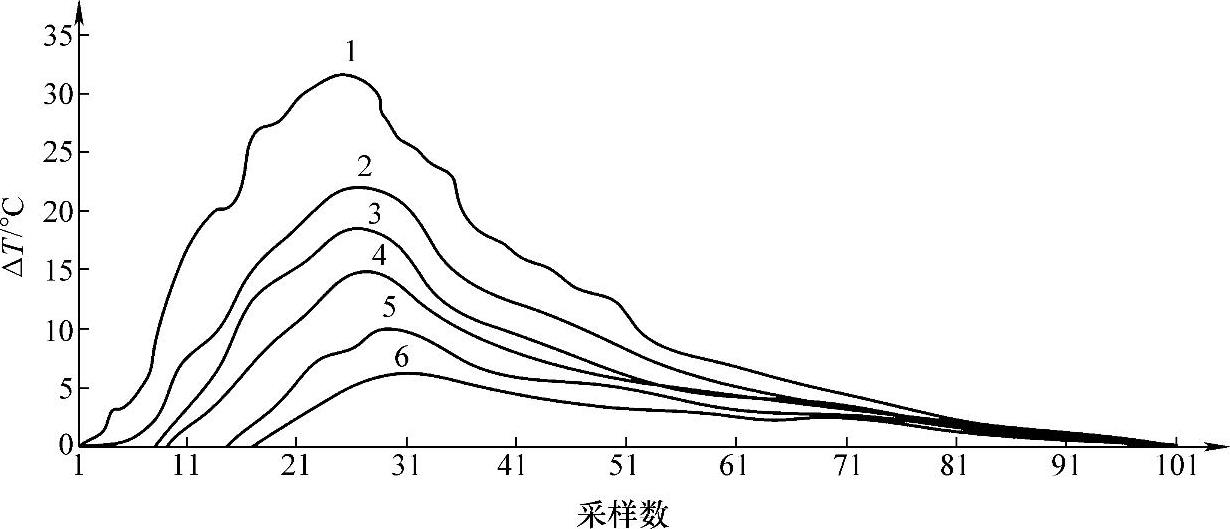
图4-43 各测量点温度变化过程

图4-44所示为热膨胀与温变及采样（时序）关系图。由图4-44各测点a图可以看出：在1、2测点温度变化（图中细线）在前、热变形（图中粗线）滞后，从测点3开始热变形在前、温度滞后，故在测点2与测点3点之间有同步点。由图4-44各测点b图可知，1、2测点温度上升在下、温度下降在上，从测点3开始温度上升在上，而且测点2和3温度上升线和下降线最靠近。在测点2与测点3之间有温度上升和下降线。

在测点2和测点3之间应该存在一个用于精确估计热变形的最佳温度测点，其满足如下关系：

1）该点处温度变化与主轴热变形接近同步，无滞后且呈近似线性关系。

2）该点处在升温过程中的曲线与降温过程中的曲线基本重合。

3）经进一步分析、计算、实测可得，该点距热源三分之一主轴长度多一点。

（3）最佳温度测点位置的热误差数学模型 采用黄金分割法和反复迭代，对最佳温度测点位置的选择加以优化。对于本次试验所用的主轴，其最佳温度点的起始搜索区间为0.25～0.42L。因为试验所采用的温度传感器直径为10mm，所以当搜索区间小于10mm时，就可以认为已找到最佳温度测点，并结束迭代过程。最后得到了最佳温度测点位置为0.372L。采用回归分析和最小二乘法对最佳温度测点的ΔT-ΔL曲线进行拟合，取置信度为99%。拟合直线及其残差如

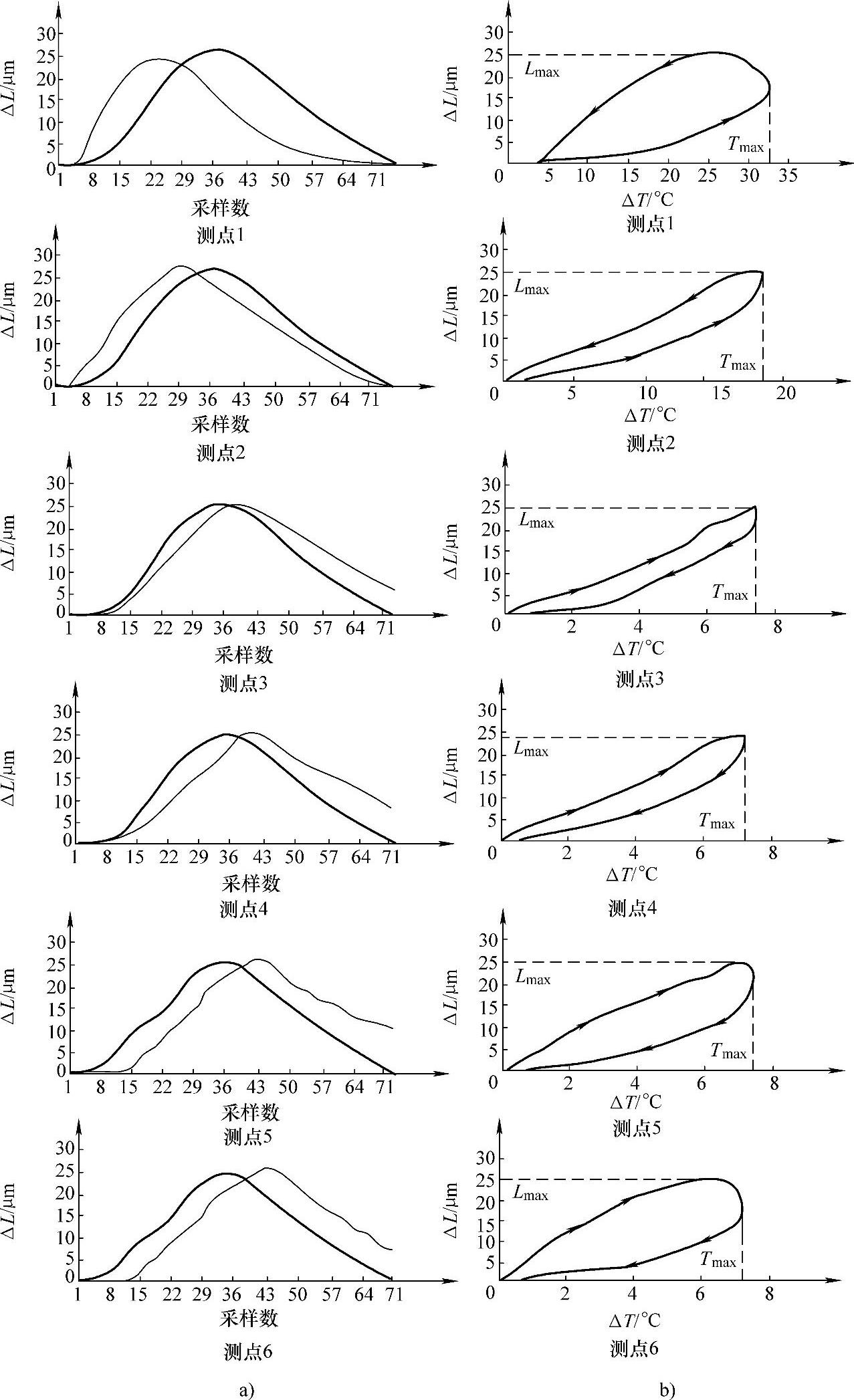
图4-44 热膨胀与温变及采样（时序）关系

a）热膨胀与采样的关系 b）热膨胀与温度的关系

图4-45所示，从图4-45中可以看出，采用最佳温度测点预测机床主轴的热伸长量时所产生的残差仅3.5μm，其曲线方程为

ΔL=2.47ΔT-4.02

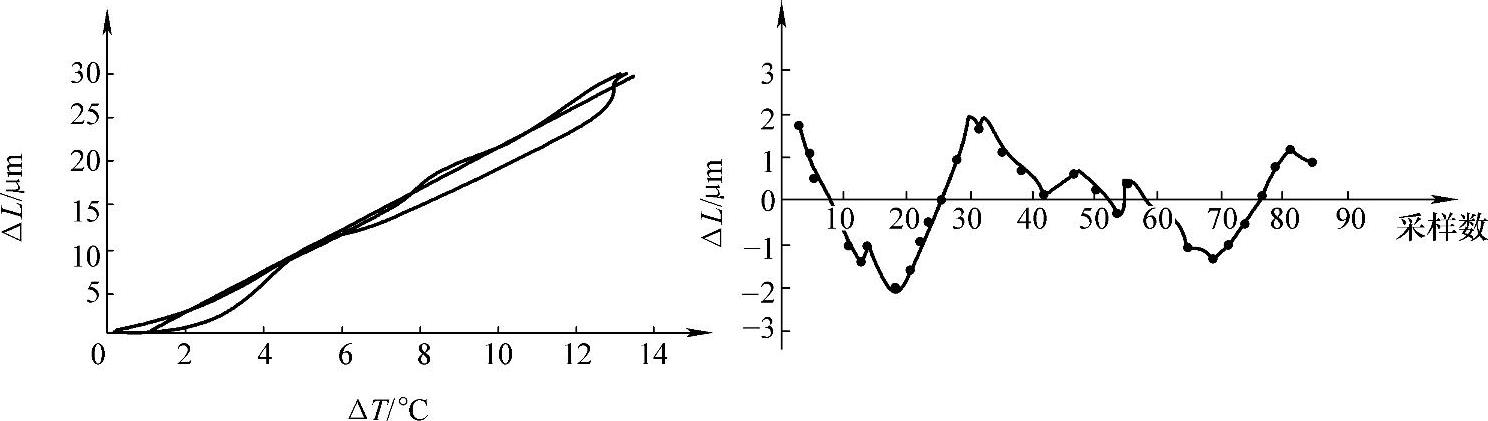
图4-45 最佳温度点分析图

在机床热误差建模和补偿过程中采用此最佳测点位置的温度变化读数可以最优地预计主轴（轴向）热变形，即不仅可以建立精度高和鲁棒性强的热误差模型，实现有效的实时误差补偿，还可以大大减少温度传感器的数量，提高测量的效率，减少实施成本并方便应用，从而产生更好的机床热误差实时补偿效果，使数控机床的加工精度大幅度提高。

图4-46所示为机床主轴两端热源时各位置上ΔT和ΔL之间的关系图。由图4-46可知，主轴两端热源与单端热源情况相近。

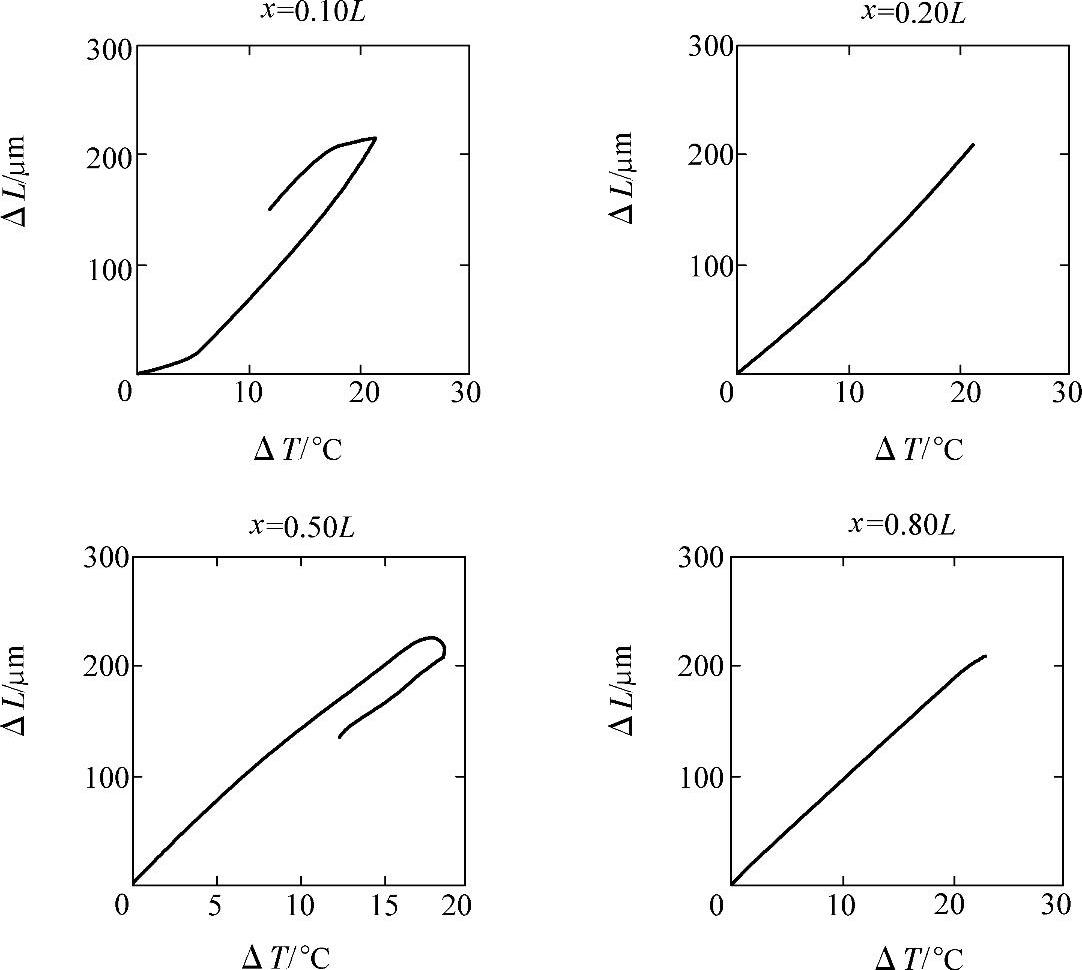
图4-46 主轴两端热源时各位置上ΔT和ΔL之间的关系图

图4-47所示为圆盘最佳温度测点位置。通过试验得出，圆盘最佳温度测点位置R_opt=0.35R。

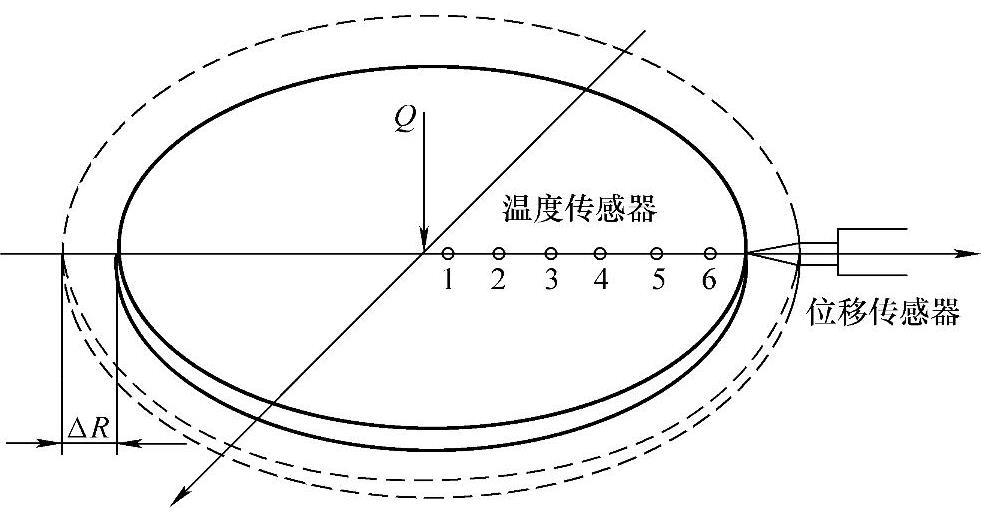
图4-47 圆盘最佳温度测点位置