双球规检测机床误差方法

1.双球规法

双球规法是ISO230-4：2005中所推荐的一种方法。1982年，J.B.Bryan在美国Lawrence Livermore国家实验室，首先开发出了用于快速检测数控机床运动误差的双球规。如图4-14所示，双球规由两个精密金属圆球和一个可伸缩连杆组成，在连杆中间镶嵌着用于检测位移的光栅尺。

测量时，一个圆球通过与之只有三点接触的磁性钢座固定在工作台上，另一个圆球通过同样的装置安装在主轴上，两球之间用连杆相连接。当机床在XY平面上作圆插补运动时，固定在工作台上的圆球就绕着主轴上的圆球旋转。如果机床没有任何误差，则工作台上圆球的轨迹是没有任何畸变的真圆。光栅尺也就没有位移输出。而当工作台存在几何运动误差时，工作台上的圆球所扫过的轨迹并不是真圆。该圆的畸变部分被光栅尺1∶1地测量出来，再通过运动学建模，就可以得到各项误差元素。

图4-14 双球规检测

双球规可以同时动态测量两轴联动状态下的轮廓误差，数控机床的垂直度、重复性、间隙、各轴的伺服增益比例匹配、伺服性能和丝杠周期性误差等参数指标都能从运动轮廓的半径变化中反映出来。另外，利用加长杆还可以在更大的机床加工空间内进行测量。通常，测量周期不超过1h。球杆仪现已被国际机床检验标准，如ASME B5.54—2005等推荐采用。

使用反求法辨识误差元素可以减少误差检测时间。如图4-15a、b所示，六次检测可获得21项机床误差元素。

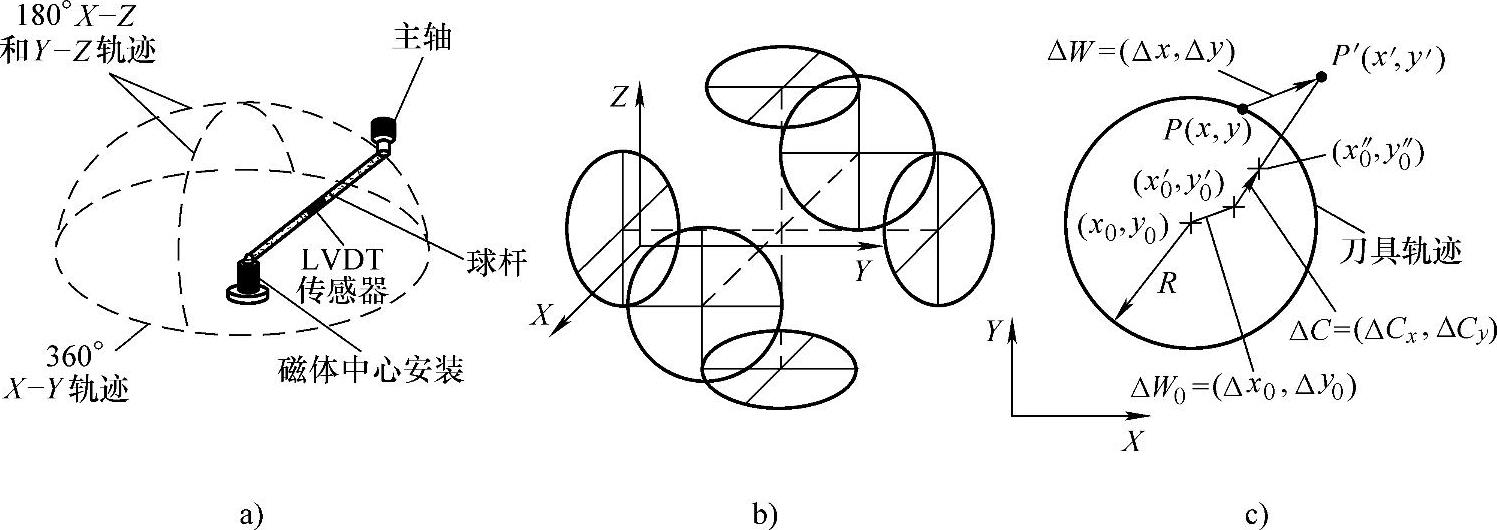
图4-15 双球规在平面的检测原理

双球规在平面的检测原理如图4-15c所示。其中，（x₀，y₀）为绝对坐标系，（x₀′，y₀′）为导轨坐标系，（x″₀，y″₀）为控制坐标系，指令位置为P（x，y），实际位置为P′（x′，y′）。理想情况下P=P′，但由于机床存在误差，此时P≠P′，理想位置与实际位置的关系如下：

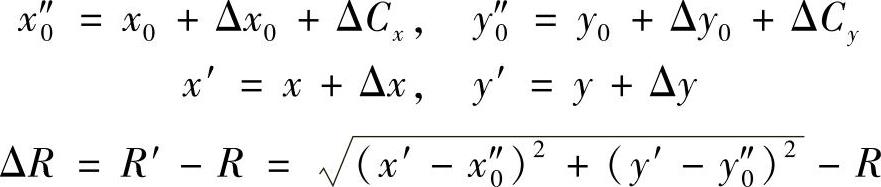
令C_x、C_y为沿X轴和Y轴的误差元素，则有

C_x=Δx₀+ΔC_x，C_y=Δy₀+ΔC_y解上述方程式，可得

ΔR=（xC_x+yC_y）/R （4-30）

2.双球规法的误差元素辨识过程

使用双球规除可辨识机床的21项几何误差元素外，还可辨识轴向标度（光栅标尺）误差、反向间隙、轮廓误差、伺服控制系统响应滞后和位置增益不匹配误差等。双球规法的误差元素辨识过程如图4-16所示。

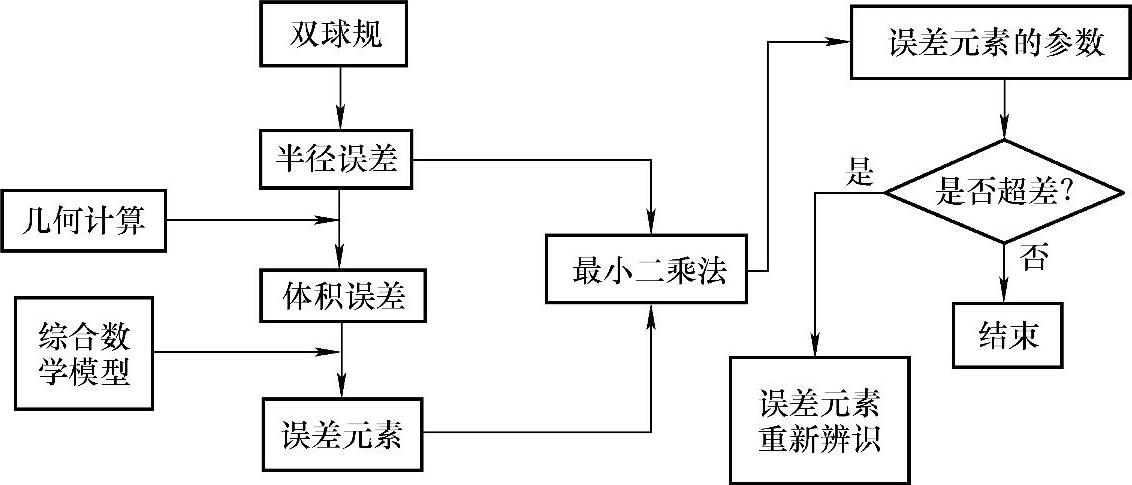
图4-16 双球规法的误差元素辨识过程

3.机床误差双球规检测

图4-17所示为机床误差双球规实际检测图。测量时，一个圆球通过与之只有三点接触的磁性钢座固定在工作台上，另一个圆球通过同样的装置安装在主轴上，两球之间用连杆相连接。机床做圆插补运动，固定在工作台上的圆球就绕着主轴上的圆球旋转。机床几何运动误差可被光栅尺1∶1地测量出来。

（1）几何误差检测 以X方向光栅标尺均匀伸长引起的误差为例，设a为标尺伸长系数，由于标尺伸长引起的X向误差C_x=aX，由双球规误差计算公式（4-30）可得(www.xing528.com)

又X=Rcosθ；Y=Rsinθ

所以有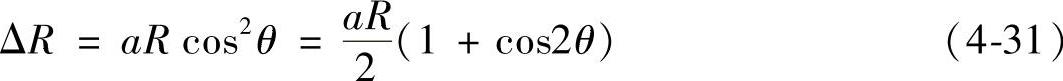

于是，得到光栅标尺均匀伸长引起的误差。同理，根据相应的几何误差模型，可以得到垂直度误差、环路增益不匹配误差、螺距误差、间隙误差、直线度误差等。

图4-17 机床误差双球规检测法

a）测量在XOY平面内的运动轨迹 b）测量在XOZ平面内的运动轨迹 c）测量在YOZ平面内的运动轨迹

（2）工作台偏摆误差典型圆轨迹 由于工作台具有偏摆误差，机床在进行整圆插补时，在工作台偏摆方向的误差突然增大，导致圆弧插补的起始位置突变，在工作台返程时（另一半的圆弧插补），导致圆弧插补的位置逆方向突变，实际圆的轨迹发生如图4-18所示的畸变。

4.定位误差元素的典型误差圆轨迹

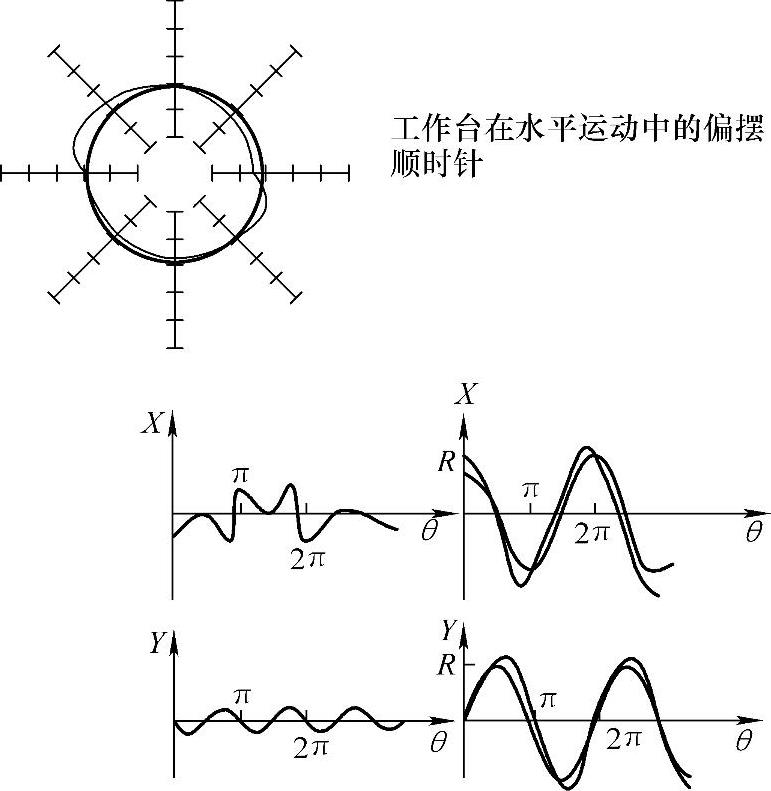
图4-18 工作台偏摆误差

图4-19 圆误差轨迹

定位误差元素的典型圆误差轨迹如图4-19和图4-20所示。图4-19所示为间隙误差所引起的圆误差轨迹，由于机床间隙的影响，圆误差轨迹为两个交错的半圆。如图4-20a所示，由于丝杠伸长，圆误差轨迹变成椭圆形（丝杠伸长）或梅花形（丝杠弯曲）。图4-20b所示为机床丝杠节距误差的圆误差轨迹及传感器噪声引起的圆误差轨迹，由该类误差引起的圆误差轨迹具有规律的间歇性波动特性。

图4-20 机床典型误差圆轨迹

a）丝杠误差 b）丝杠节距及传感器噪声误差

5.伺服控制系统误差的误差圆轨迹（见图4-21）

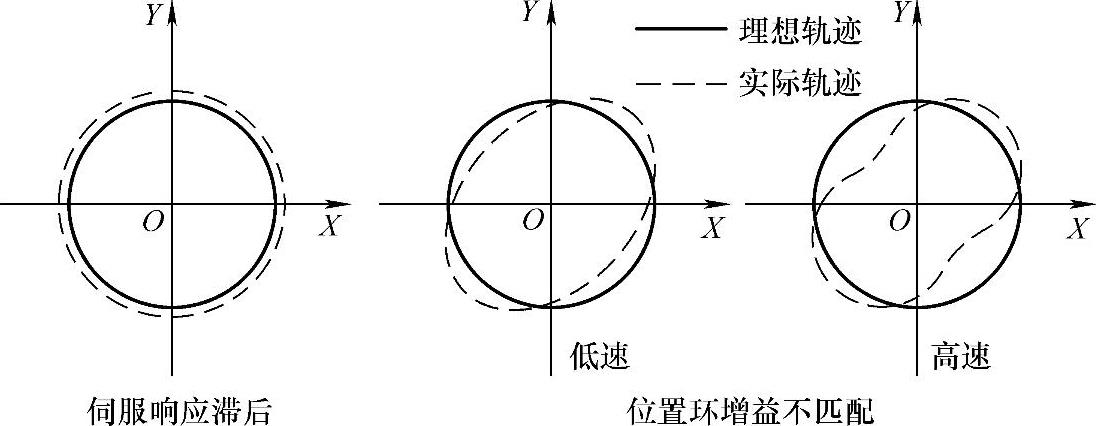
图4-21 伺服控制系统误差的误差圆轨迹