激光干涉仪检测法：原理和应用

自1960年T.Maiman发明第一台红宝石激光器以来，激光理论及技术发展迅速，各种激光器应运而生。1964年，Yeh等人首次通过测量激光的多普勒频移得到流体的速度信息，开创了应用激光测量的先河。此后，先后有各种典型的激光干涉仪器，如迈克逊（Michelson）干涉仪、泰曼格林（Twyman Green）干涉仪、麦克詹达（Mach-Zender）干涉仪、菲索（Fizeau）干涉仪、HP干涉仪、Renishaw干涉仪及多普勒双频激光干涉仪（LDDM）等纷纷应用于机床误差的检测，其中以多普勒双频干涉仪可测项目范围最广。

双频激光干涉仪是在单频激光干涉仪的基础上发展的一种外差式干涉仪。它以两个具有不同频率的圆偏振光作为光源，发射光经偏振分光镜将两个光正交分离。当测量反射镜移动时，由于多普勒效应，返回光产生多普勒频移，其包含了测量反射镜的位移信息。所以，测量信息是叠加在一个固定频差上的，属于交流信号，具有很大的增益和高信噪比，完全克服了单频激光测量仪因光强变动造成直流电平漂移致使系统无法正常工作的弊端。测量时即使光强衰减90%，双频激光测量仪仍能正常工作。由于其具有很强的抗干扰能力，因而特别适合现场条件下使用。

图4-1所示为激光干涉仪工作示意图。激光干涉仪工作时，激光头固定不动，反射镜或干涉镜随机床部件一起移动，可测距离（位置精度）、直线度、垂直度、偏摆角、平行度、平面度、转台精度及速度和加速度等，并可对机床振动情况进行分析。这些检测项目几乎包括了机床精度鉴定的所有主要指标。

1.激光干涉仪测量原理

（1）多普勒效应（Doppler Effect）任何形式的波传播，由于波源、接收器、传播介质或中间反射器或散射体的运动，会使频率发生变化，这种现象即多普勒效应。这种因多普勒效应所引起的频率变化称多普勒偏移或频移（Doppler Shift），频移大小与介质、波源和观察物的运动有关，如图4-2所示。

（2）线性位移误差检测原理 如图4-3所示，激光头射出的频率为f₀，经平行反射镜反射来到侦测器，当平行反射镜不动时，其反射波频率f_r=f₀。当反射镜以v（=dx/dt，远离时取“+”，移近时取“-”）的速度移动时，因为光程增加（或减少）了2vt，反射波f_r的数值会减少（或增加）2v/λ₀（λ₀为激光的波长），即

Δf=f₀-f_r=2v/λ₀=（2/λ₀）dx/dt （4-1）

而f=ω/2π，且ω=dφ/dt

故

即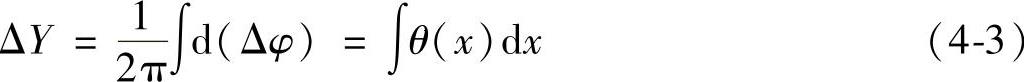

求得 N+Δφ/2π=（2/λ₀）x （4-4）

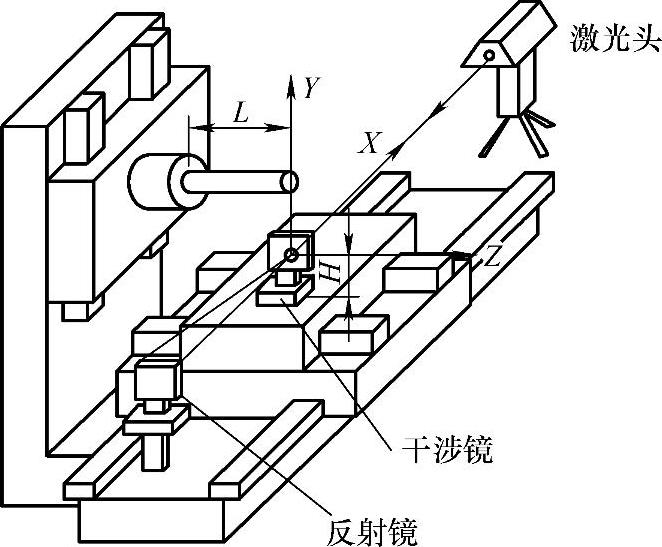
图4-1 激光干涉仪工作示意图

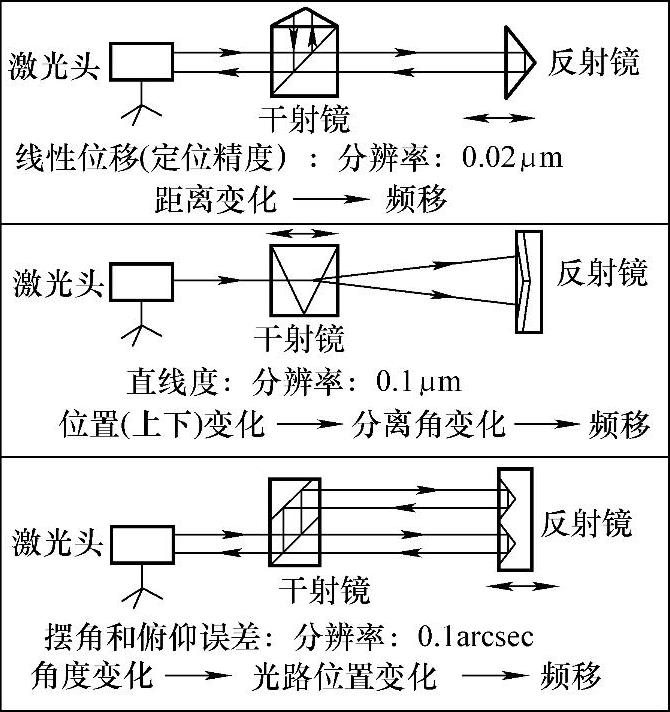
图4-2 多普勒效应

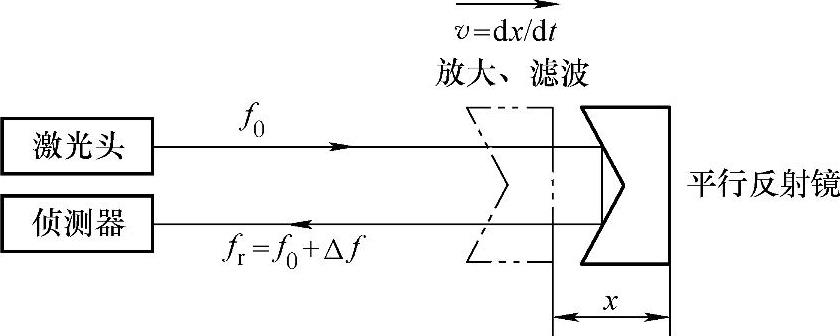
图4-3 激光多普勒频差效应原理

式中N——式（4-3）左边积分满一周期（即2π）的周数；

Δφ/2π——未满一周期的余量；

ω——圆频率；

φ——相位；

Δφ——相位差；

ΔY——增加或减少的反射波；

θ（x）——中间变量，θ（x）=2/λ₀。

由式（4-4）可得

x=（λ₀/2）（Δφ/2π+N） （4-5）

根据式（4-5），激光多普勒测量仪采用了一个鉴相器，每当相位φ积满一个2π，鉴相器便输出一个增位（或减位）脉冲，即式（4-5）中的N。另外，以0到15V的模拟电压表示Δφ/2π这一项。计算鉴相器的脉冲数以及模拟电压的伏数，根据式（4-5）便可测知位移x。

（3）转角误差检测原理 以检测X轴沿Y方向的转角误差（角偏）为例，如图4-4所示，将一个双光束激光多普勒测量仪的激光射向一个双晶平行反射镜。双晶平行反射镜随机床X轴移动，当机床床身在移动时发生了一个水平方向的角偏θ，则双光束激光的光程X₁、X₂就起了变化（X₁≠X₂）。它们之间的关系为：tan（θ）=（X₂-X₁）/d，当角偏很小时。tan（θ）=θ，即

θ=（X₂-X₁）/d （4-6）

式中d——双晶平行反射镜的中心距离。

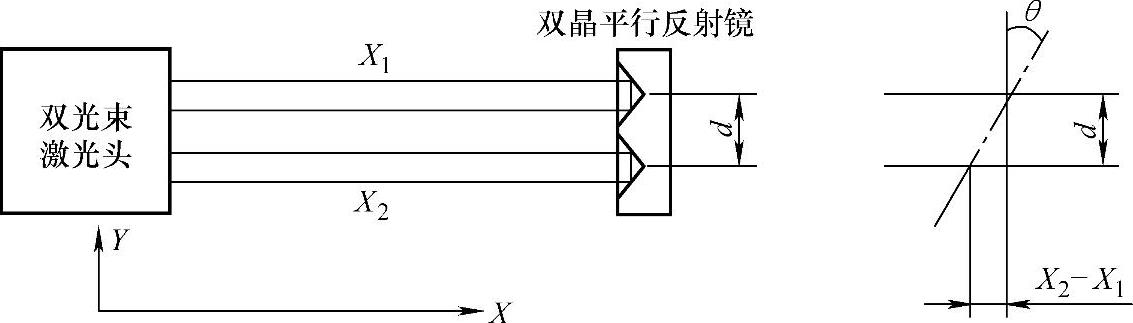
图4-4 角偏测量

这样，通过测量两条光线的光程差便可测出角偏。而机床移动时横向偏移则是

如果把机床的运动起点和终点当作一直线，则式（4-7）中的ΔY就是机床沿X轴移动时在Y方向的直线度误差。

当把双光束激光头和双晶平行反射镜直立（即沿垂直方向）架设时，就可以测量机床移动时沿垂直方向（Z方向）的角偏（即俯仰误差）和直线度误差。

2.机床误差的体积测量方法

目前，国内外学者就利用激光干涉仪测量机床的几何误差提出了多种测量及辨识方法，如22线法、15线法、14线法、9线法等。但是，在实际测量时，这些方法大都过于复杂，测量周期太长，调整极度困难和费时，而且需要附加购买昂贵的光学元件。对于机床空间位置精度的检定，美国国家标准中推荐了一种通过测量机床体对角线的位移误差的快速检定、评价方法。所谓体对角线就是指在空间直角坐标系中，由机床工作台三个进给方向上的最大行程所围成的长方体的四条对角线。这种方法的确改进了机床误差测量过程，但是采用这种测量方法无法获得足够的信息用于分析误差源，因此也无法获得用于误差补偿的有关信息。

我们通过与美国光动公司合作，提出了一种基于激光矢量多步法的沿体对角线的机床空间位置误差体积测量方法，实现了机床空间位置误差的高效测量和机床空间位置精度的快速检定，并可通过测量数据进行补偿。该方法是一种机床误差元素的高效、快速测量方法。如图4-5所示，利用激光多普勒位移测量仪，通过对机床工作运动空间的四条对角线进行分步运动的位移测量，并使用一定算法就可以分离或辨识出机床三根运动轴的三项定位误差、六项直线度误差和三项垂直度误差，共计12项移动性误差元素。另外，还可利用测量数据进行补偿。而且，如果附加测量两条平面对角线及一条平面直线的运动位移误差则可以辨识出三轴机床的九项转角误差元素。

图4-5 机床误差的体积测量方法

（1）激光矢量多步法的测量过程 如图4-6所示，大平镜安装在机床主轴上，并与激光束方向垂直。测量时走四条体积对角线，走每条对角线时，走一次分三步，x、y和z先后分别走一个步距：dx、dy和dz（见图4-7），每走一个步距可获得包含一个位移误差和两个直线度误差信息的数据，走完一条对角线可获得包含三个位移误差、六个直线度误差和三个垂直度误差共12项移动性误差元素信息的数据。故多步矢量测量可获得比其他激光测量多三倍的测量数据。

图4-6 多步法激光测量过程

（2）多步法矢量测量的误差的辨识 机床误差的辨识就是通过误差的数学建模，将误差元素进行分离获得各项误差。机床几何误差辨识主要是基于激光多普勒位移测量仪（Laser Doppler Displacement Meter，LDDM）技术和创新的多步测量及其算法，利用简单的激光头与套件即可从仅四次多步调整测量中（沿机床四个对角线方向），快速地辨识出机床的全部12项移动误差，不但调整操作简单方便且节省大量时间，为误差补偿的应用创造了更有利的条件。

如图4-8所示，测量空间分段路径共八条来回对角线分别为PPP、NPP、PNP、PPN、NNN、PNN、NPN及NNP。其中，三个字母依次表示为X、Y、Z向，N——Negative（反向）、P——Positive（正向），如PPP就是指向三个轴的坐标都增加方向的对角线。激光矢量多步法测量的行程如图4-9所示。

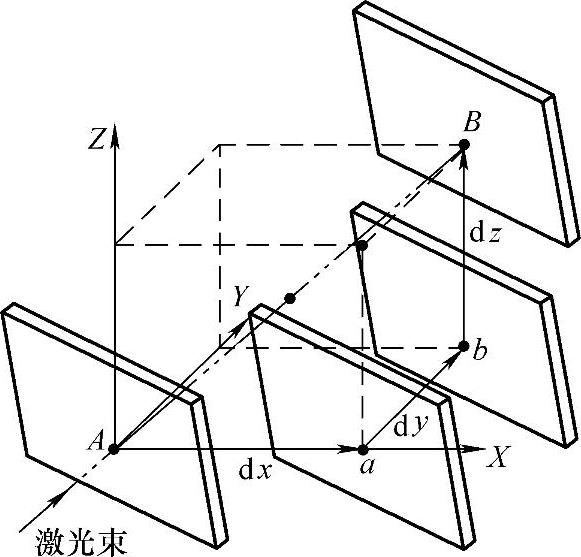
图4-7 激光测量多步法原理

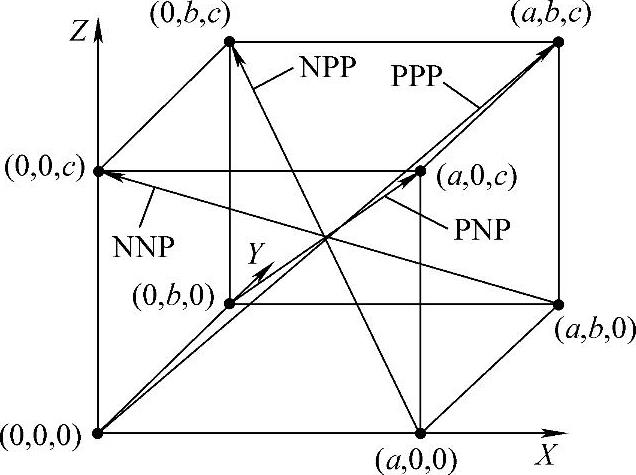
图4-8 空间体积测量路径

如图4-10所示，设三维空间为a×b×c，测量点的坐标为（x₀，y₀，z₀）。首先通过空间解析几何方法，求解测量点在对角线上投影点（x_p，y_p，z_p），为此将直线方程参数化，设参数为t，则对角线的直线参数方程为

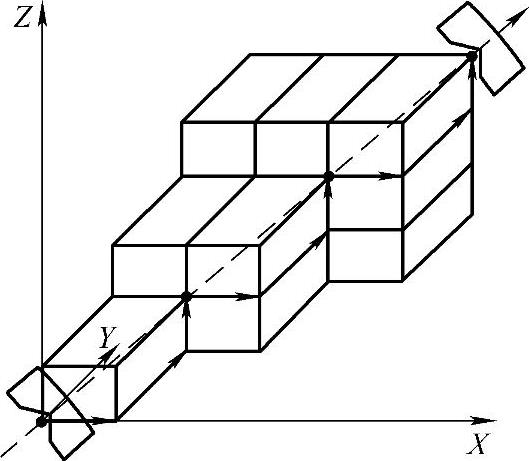
图4-9 激光矢量多步法测量的行程

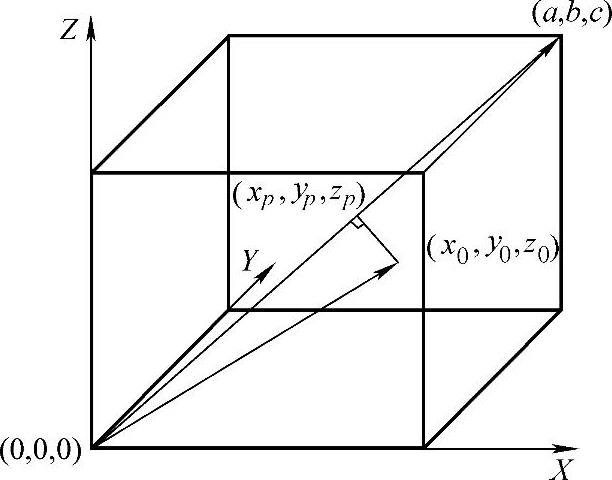
图4-10 三维空间中测量点在体对角线上的坐标

代入平面方程，则有

a（at-x₀）+b（bt-y₀）+c（ct-z₀）=0 （4-9）

解得参数t的值为

则交点坐标为

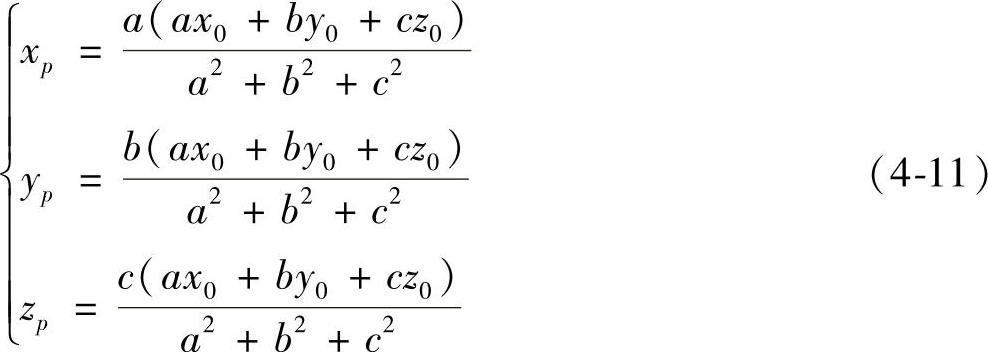(www.xing528.com)

在对角线测量得到的值R为

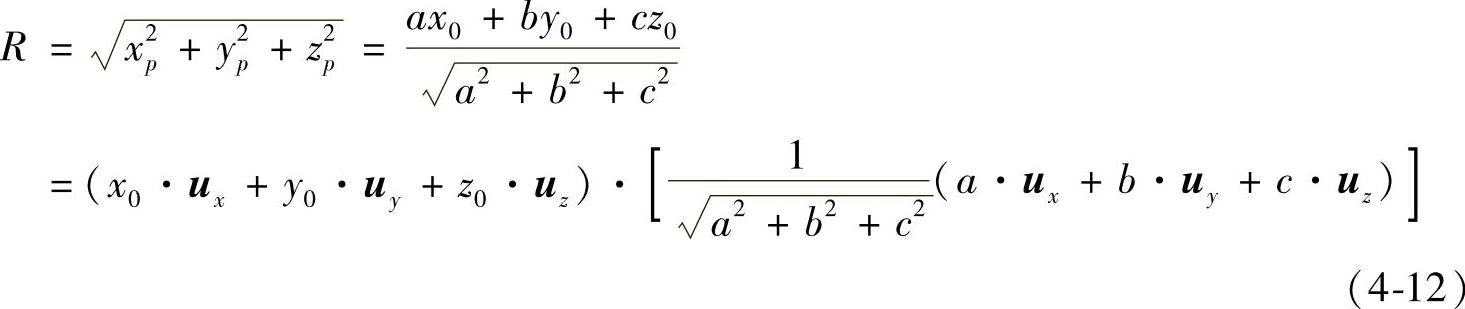
所以，测量点在空间对角线上的测量值为该点的矢量（x₀·u_x+y₀·u_y+z₀·u_z）与测量对角线方向单位矢量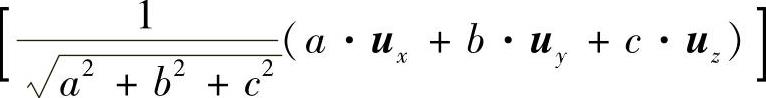的乘积。

假设实际测量点和理想测量点在空间存在三个方向的误差Δx、Δy、Δz，即实际测量点坐标为（x+Δx，y+Δy，z+Δz），可以得到理想测量点和实际测量点在体对角线上测量值误差为

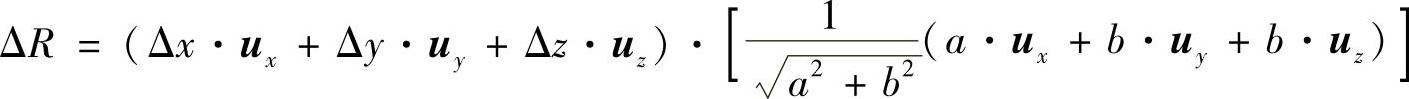
（4-13）

如果沿空间体对角线进行机床空间定位误差的测量，则三维空间的误差（Δx，Δy，Δz）可以在对角线误差ΔR中反映出来，也就是说对角线误差对空间误差都具有敏感性。

因此，可以定义数控机床空间定位误差的对角线测量的一般公式为

ΔR=e·r （4-14）

式中 e——定位误差的误差矢量，e=Δx·u_x+Δy·u_y+Δz·u_z；

Δx、Δy、Δz——机床在x、y、z方向上产生的误差值，并与第3章综合误差建模

结果中的Δx、Δy、Δz对应（本节在只考虑几何误差的情况

下）；

r——空间体对角线方向的单位矢量，由机床工作空间的大小决定。

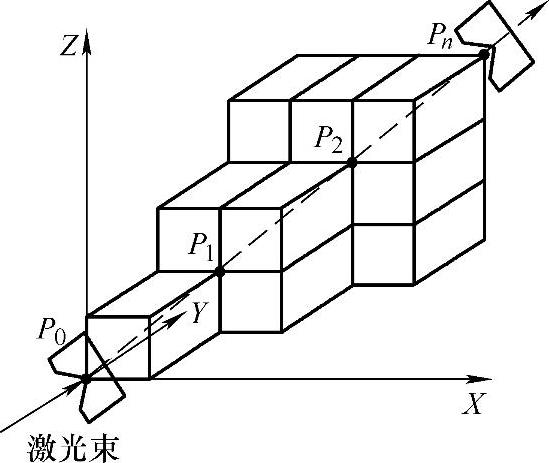
图4-11 机床体对角线的测量

在进行对角线测量时，首先将对角线分为n个测量点，如图4-11所示。假设体对角线的起点为（x_s，y_s，z_s），终点为（x_e，y_e，z_e），则各个连续测量点在X、Y、Z轴上的坐标变化量D_x、D_y、D_z分别为

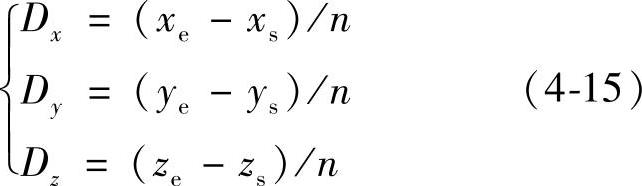
因此，在对角线方向的单位矢量可以表达为

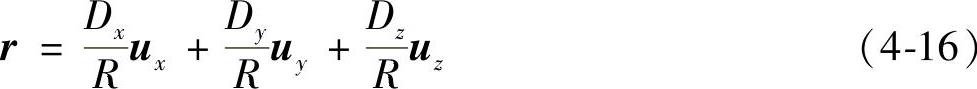
式中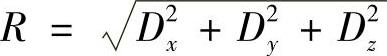

这样，机床误差在对角线上所反映的测量误差值可以由式（4-14）得到，其中误差e=Δx·u_x+Δy·u_y+Δz·u_z，Δx、Δy、Δz为机床在x、y、z方向上产生的误差值。对于XYTZ型数控机床，沿体对角线PPP的测量误差dR_PPP为

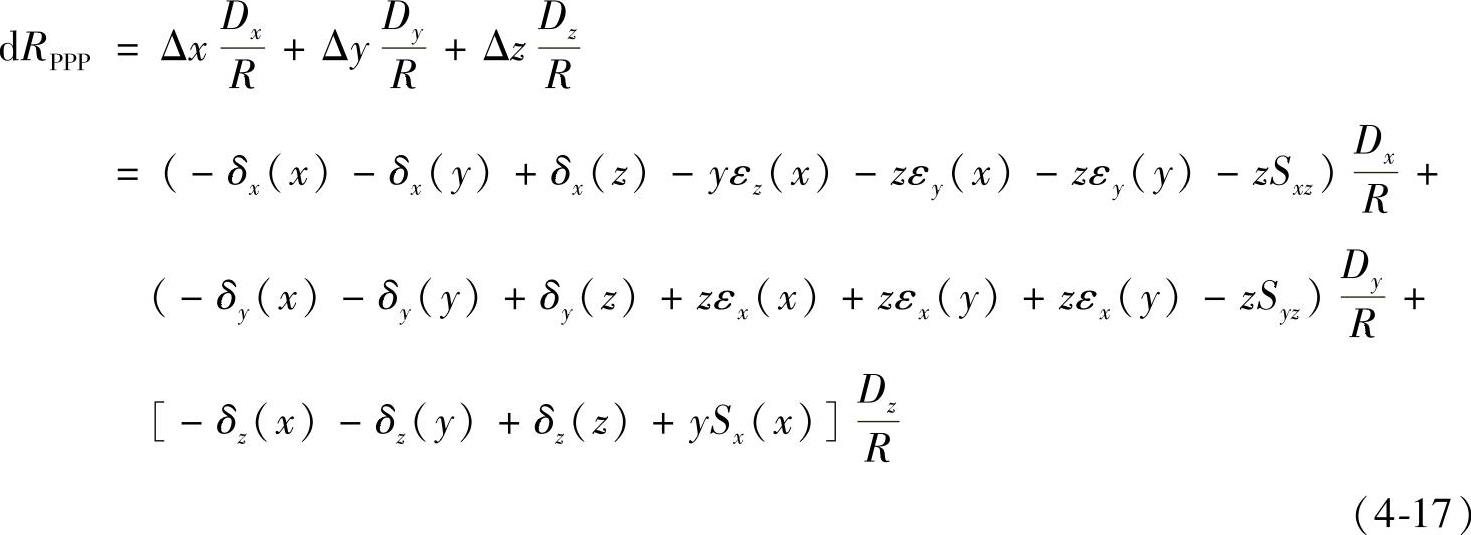
同理，沿体对角线NPP的测量误差dR_NPP为

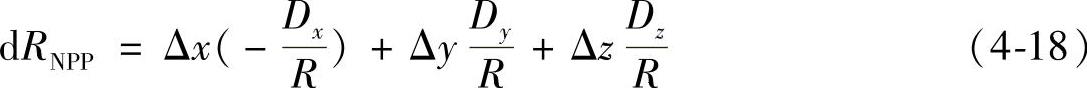
沿体对角线PNP的测量误差dR_PNP为

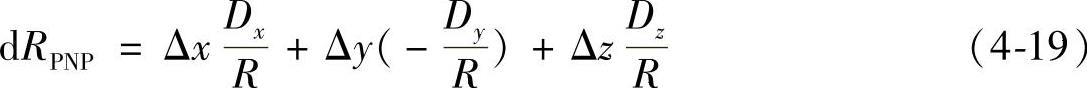
沿体对角线PPN的测量误差dR_PPN为

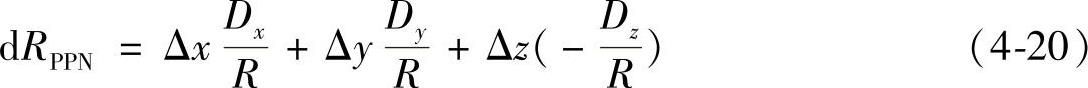
由式（4-17）～式（4-20）可见，沿四条体对角线的测量误差具有对所有误差源（定位误差、直线度误差、垂直度误差及转角误差）都敏感的特性。

分步体对角线测量法的原理如图4-12所示。假设P₀和P₁分别为机床工作空间对角线上的两个测量点，且D_x、D_y、D_z分别为这两个测量点之间的坐标变化量。在一般体对角测量方法中，首先在P₀点测得这时的对角线数据值R₀，然后通过机床X、Y、Z轴的联动达到下一测量点P₁，并测得该位置的对角线数据R₁，两次测得的对角线之差为ΔR。

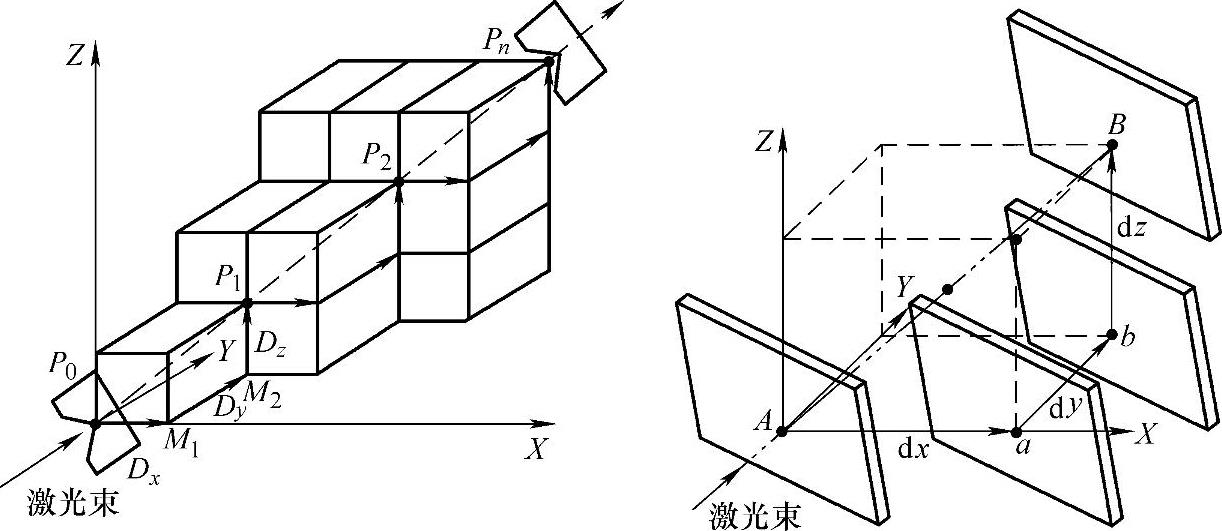
图4-12 分步体对角线测量法的原理

在本章应用的分步体对角线测量中，当P₀点处的对角线数据值R₀测量之后，第一步，通过X轴运动增量D_x到达中间点M₁处，并测得对角线数值R_M1；第二步，再通过Y轴运动增量D_y到达中间点M₂处，并测得对角线数值R_M2；第三步，通过Z轴运动增量D_z到达常规体对角线的第二个测量点P₁处，并进行对角线测量得到值R₁。因此，分步体对角线测量与一般体对角线测量的主要差异是将P₁和P₀点处的坐标变化量D_x、D_y、D_z转换成了X、Y、Z轴分别进行运动时的运动增量，并增加了中间点M₁和M₂的对角线测量值R_M1和R_M2，对于同样运动到对角线上的下一个测点，测量数据增加为原来的三倍。对于机床工作空间的四条体对角线，可以测得12组数据。可以看出，这种分步体对角线测量方法比常规体对角线测量法方法可以获得更多的信息。

设机床沿X、Y、Z轴分别运动之后产生的误差为E（x，y，z），则每一个方向的误差为

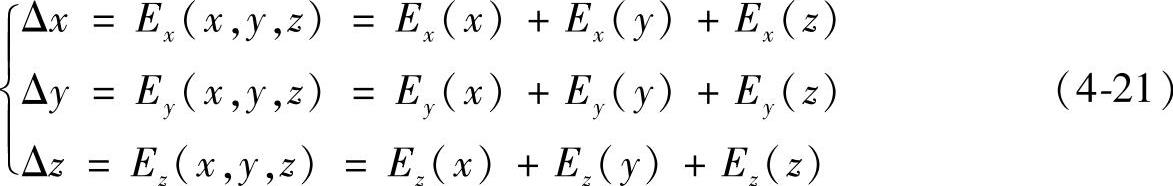
式中E_x（x，y，z）、E_y（x，y，z）、E_z（x，y，z）——机床分别沿X、Y、Z轴运动后在x、y、z方向上产生的误差值。

E_x（x）、E_y（x）、E_z（x）——沿X轴移动时在x、y、z方向上产生的空间定位误差值，其下标表示误差的方向，括号内的值表示运动方向。

需要说明的是，E_x（x）、E_y（x）、E_z（x）这些误差值是沿X轴运动产生的误差的综合，包括了定位误差、直线度误差、转角误差和垂直度误差的影响。同理，E_x（y）、E_y（y）、E_z（y）分别为沿Y轴运动在x、y、z方向上产生的空间定位误差，E_x（z）、E_y（z）、E_z（z）分别为沿Z轴移动时在x、y、z方向上产生的空间定位误差。

式（4-21）将空间定位误差在各方向上的误差进行了分解，将式（4-21）代入式（4-17），可得

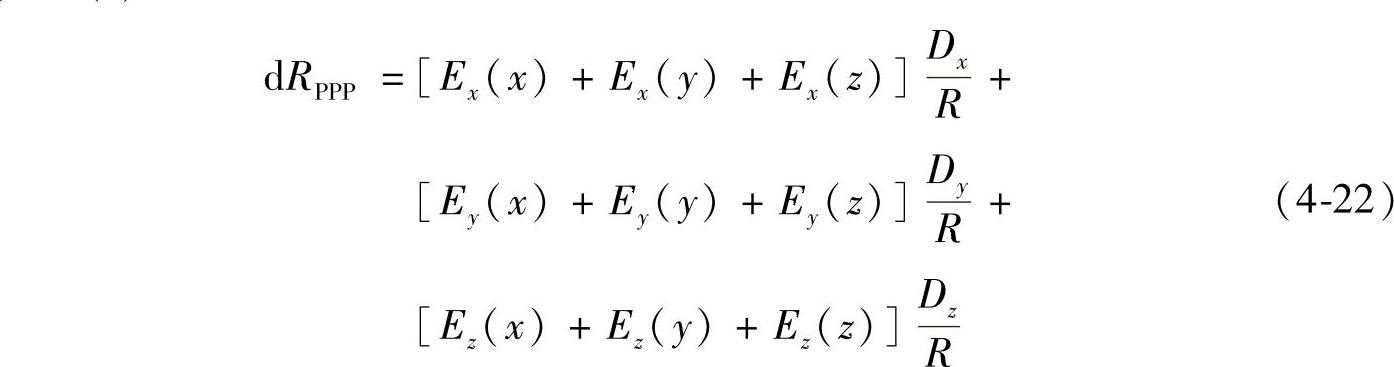
在分步体对角线测量过程中，体对角线PPP上产生的误差记为dR_PPP，则沿着X、Y、Z轴在x、y、z方向分步运动后的误差元素分别记为dR_PPP（x）、dR_PPP（y）、dR_PPP（z），则有

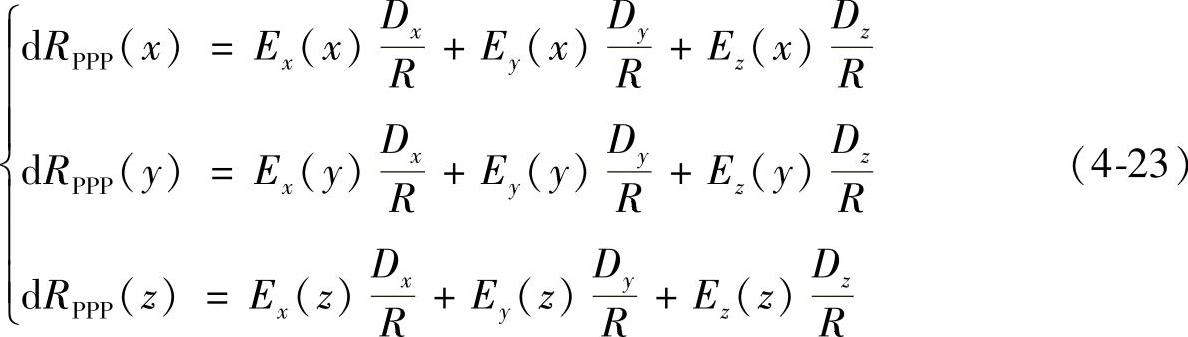
同理，对于另外三条对角线，也可以得到在x、y、z方向运动时在对角线NPP产生的误差dR_NPP（x）、dR_NPP（y）、dR_NPP（z）：

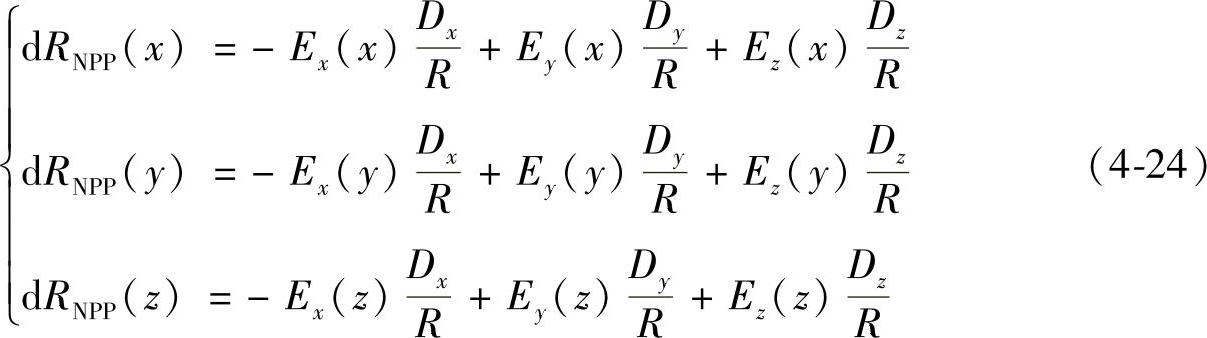
在x、y、z方向运动时在对角线PNP产生的误差dR_PNP（x）、dR_PNP（y）、dR_PNP（z）：

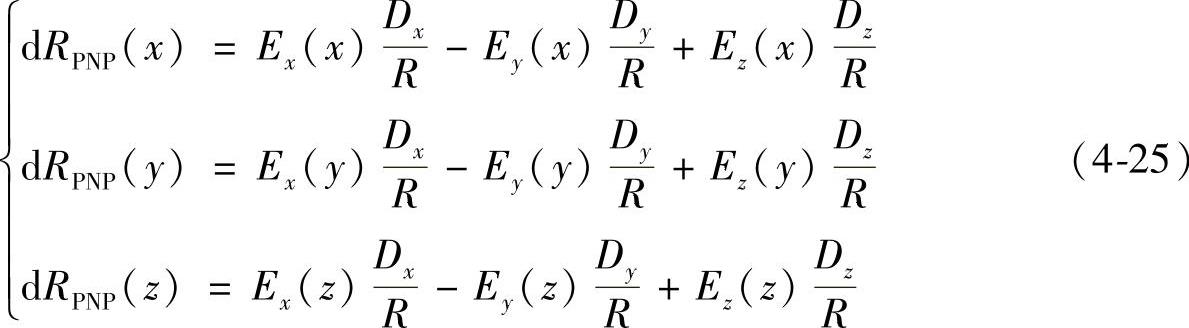
在x、y、z方向运动时在对角线PPN产生的误差dR_PPN（x）、dR_PPN（y）、dR_PPN（z）：

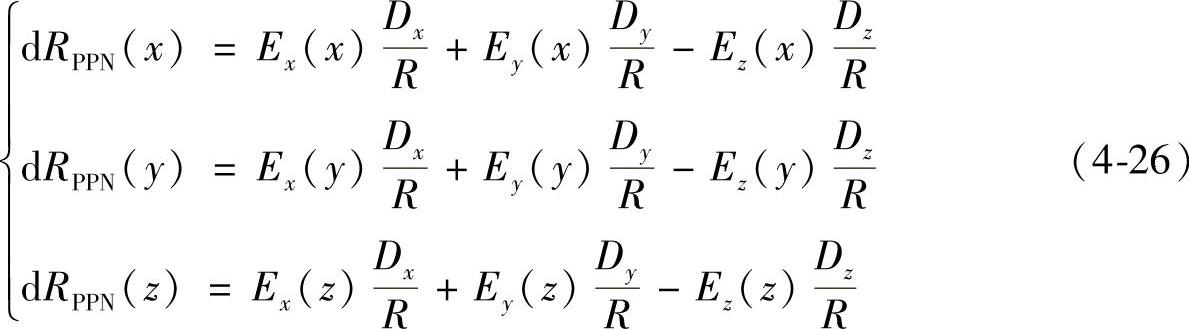
根据式（4-23）～式（4-26）四组公式，求解各轴进给运动后分别在x、y、z方向产生的位置误差E_x（x）、E_y（x）、E_z（x），E_x（y）、E_y（y）、E_z（y），E_x（z）、E_y（z）、E_z（z）共九项误差，得到X轴进给运动后在x、y、z方向产生的位置误差E_x（x）、E_y（x）、E_z（x）为

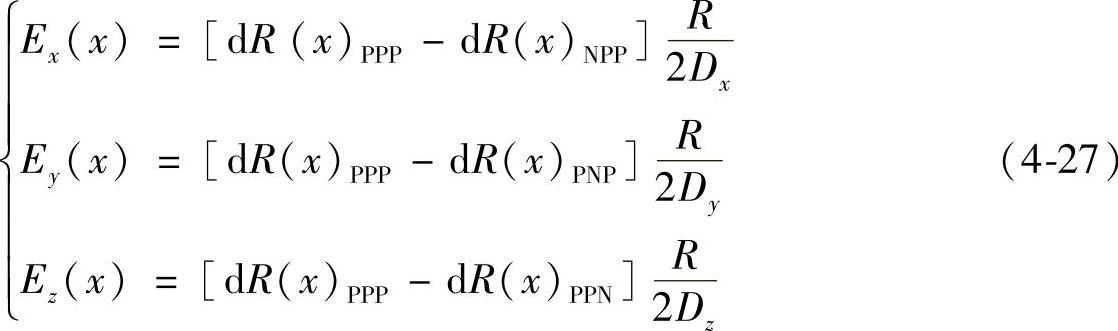
Y轴进给运动后在x、y、z方向产生的位置误差E_x（y）、E_y（y）、E_z（y）为

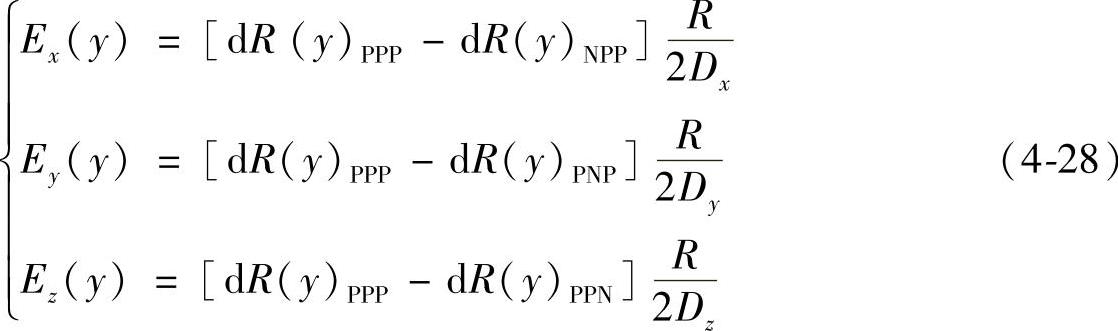
Z轴进给运动后在x、y、z方向产生的位置误差E_x（z）、E_y（z）、E_z（z）为

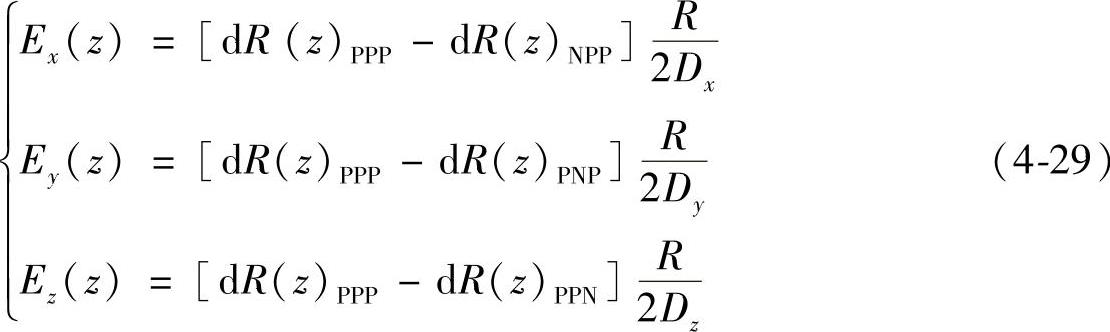
分步体对角线方法相对于传统的对角线空间定位精度校验方法的优点在于，通过沿对角线方向进行X、Y、Z轴分别进给增量D_x、D_y、D_z后进行分步测量，获得了更多的信息，通过求解得到X、Y、Z各轴在x、y、z方向进给运动后分别在x、y、z方向产生的九项位置误差E_x（x）、E_y（x）、E_z（x）、E_x（y）、E_y（y）、E_z（y）、E_x（z）、E_y（z）、E_z（z）。这九项位置误差是一个综合误差，包含了各轴运动时产生的所有误差，包括三个定位误差、六个直线度误差、九个转角误差、三个垂直度误差的影响。

考虑到转角误差相对于移动误差比较小，通过上述公式最后可解得三个定位误差、六个直线度误差、三个垂直度误差，共计12项误差元素。

3.近代自由曲面检测技术

传统测量装置或测量样板由于价格昂贵、测量效率低、测量精度低等缺点已越来越难适应机械制造高精度、高效率、高柔性的要求。随着计算机技术及光学技术等先进技术的不断发展，坐标测量仪及用于测量的智能机器人在精密加工与检测中发挥了越来越大的作用。坐标测量仪可获得较高的测量精度，但是测量时间长且容易引起工件变形。近来随着智能机器人技术的发展而发展起来的智能激光检测机器人，由于具有高柔性、高效率、无工件变形等优点，在精密加工与精密制造中发挥越来越重要的作用，如图4-13所示。

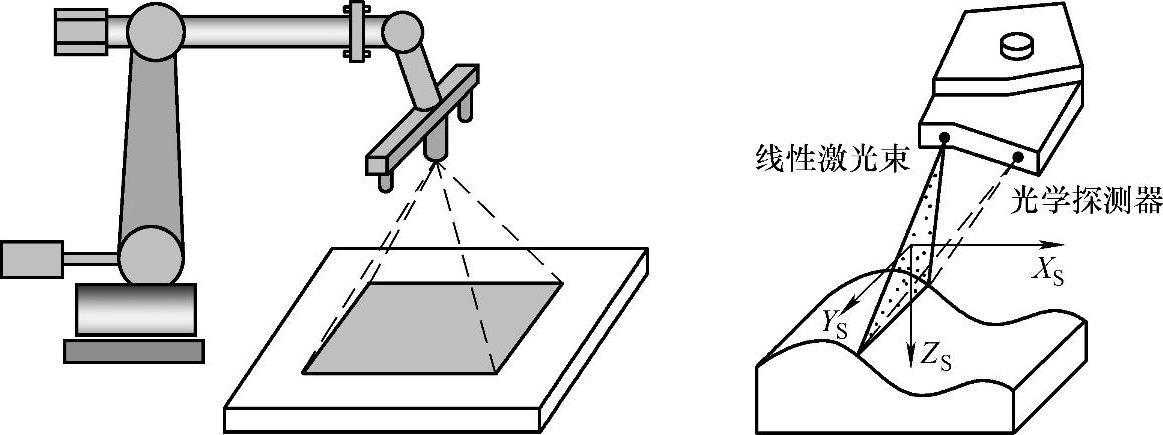
图4-13 智能激光检测机器人