统一数学模型：四种结构加工中心优化

由3.2节四种结构加工中心综合数学模型的建模过程可知，四种结构加工中心的坐标系变换均是从工件坐标系W变换到刀具坐标系T，即

式中n——从工件坐标系到刀具坐标系之问的传动链数目；

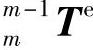——从上一传动链到下一传动链的坐标变换矩阵。

由于加工中心结构不同，各传动链的顺序如下：

TXYZ型传动链：W→R→X→Y→Z→S→T。

XTYZ型传动链：W→X→R→Y→Z→S→T。

XYTZ型传动链：W→X→Y→R→Z→S→T。

XYZT型传动链：W→X→Y→Z→R→S→T。(www.xing528.com)

从四种结构加工中心传动链可知，在进行坐标系变换时，参考坐标系位置发生规律变化，在参考坐标系R右侧坐标系齐次变换矩阵为正变换，而在参考坐标系R左侧坐标系变换矩阵为逆变换（即坐标变换方向相反）。根据这一规律，在齐次变换矩阵中加入一变量，使各坐标系变换矩阵在不同传动链中分别相应取正变换或逆变换，为此引入奇异函数：

式中i——四种结构加工中心，i=0，1，2，3，分别对应TXYZ、XTYZ、XYTZ、XYZT，即当机床结构为TXYZ时，i=0，其余类推；

T_m——变换矩阵T_X、T_Y、T_Z，取T_X=0、T_Y=1、T_Z=2。

将式（3-42）分别代入式（3-10）、（3-11）、（3-12）和（3-13）可得

将相关坐标转换矩阵代入式（3-15），基于小误差假设并忽略二阶及二阶以上小量，可得四种结构加工中心统一数学模型：

式中i——四种结构加工中心，i=0，1，2，3，分别对应TXYZ、XTYZ、XYTZ、XYZT，即当机床结构为TXYZ时，i=0，其余类推；