四种结构加工中心的综合模型分析

如图3-4所示，加工中心的四种结构分别为TXYZ、XTYZ、XYTZ和XYZT。其中，字母T表示刀具，X、Y、Z表示坐标轴，T前面的各字母表示工件相对于固定基座的运动方向，T后面的字母表示刀具相对于固定基座的运动方向。

图3-4 四种结构加工中心

TXYZ型加工中心综合数学模型已经在3.2.1建立，下面建立其他三种结构加工中心综合数学模型。

1.XTYZ型加工中心的综合数学模型

（1）设定坐标系XTYZ型加工中心结构如图3-5所示，假定机床在初始状态下，在机床床身上创建参考坐标系R，分别在X、Y、Z向工作台，主轴S，刀具T，工件W上分别创建局部坐标系X、Y、Z、S、T、W，方向与参考坐标系R一致，如图3-5所示。

图3-5 XTYZ型加工中心的坐标系设定

（2）误差运动转换矩阵

1）理想（无误差）状态下各运动轴的转换矩阵。在理想情况下，设X、Y、Z工作台分别移动距离x、y、z，则坐标系X到参考坐标系R的齐次变换矩阵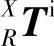、参考坐标系R到坐标系Y的齐次坐标变换矩阵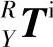和坐标系Y到坐标系Z的齐次变换矩阵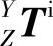分别为

理想状态下主轴和Z轴无相对运动，因此坐标系Z到主轴坐标系S的齐次变换矩阵为单位矩阵，即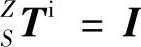；刀具与主轴固连，因此主轴坐标系S到刀具坐标系T的齐次变换矩阵为单位矩阵，即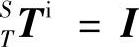；工件与X工作台之间无相对运动，因此工件坐标系W到坐标系X的齐次变换矩阵为单位矩阵，即。

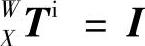在理想情况下，当机床分别沿X、Y、Z方向移动x、y、z距离时，工件坐标系W到刀具坐标系T的变换矩阵为

可知在理想情况下，刀尖（理论切削点）在工件坐标系中的坐标为（-x，y，z）。

2）实际状态（有误差）下各运动轴的转换矩阵。在实际情况下，工作台X轴存在三个移动误差δ_xx、δ_yx、δ_zx，三个转角误差ε_xx、ε_yx、ε_zx，当工作台X移动距离x时，工作台X到参考坐标系R的齐次变换矩阵为

当工作台Y移动距离y时，由于存在三个移动误差δ_xy、δ_yy和δ_zy，三个转角误差ε_xy、ε_yy、εzy^和一个垂直度误差S_xy，参考坐标系R到工作台Y的变换矩阵为

当Z移动距离z时，由于Z轴移动时存在三个移动误差δ_xz、δ_yz和δ_zz，三个转角误差ε_xz、ε_yz、ε_zz，两个垂直度误差S_xz、S_yz，则坐标系Y到坐标系Z的转换矩阵为

由于实际状态下，刀具与主轴无相对运动，因此主轴坐标系S到刀具坐标系T的齐次变换矩阵为单位矩阵，即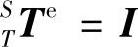；由于数控机床主轴的制造精度较高，由主轴引起的误差较小可忽略不计，因此坐标系Z到主轴坐标系S的齐次变换矩阵为单位矩阵，即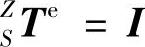：；工件与X工作台无相对运动，因此工件坐标系W到坐标系X的齐次变换矩阵为单位矩阵，即：。

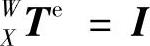在实际状态下，当机床分别沿X、Y、Z方向移动x、y、z距离时，工件坐标系W到刀具坐标系T的变换矩阵为

（3）XTYZ型加工中心综合数学模型等同TXYZ型加工中心综合数学模型的推导过程，可得XTYZ型加工中心工件坐标系W到刀具坐标系T的误差运动变换矩阵：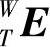

从而可得XTYZ型加工中心综合误差模型：

2.XYTZ型加工中心的综合数学模型

（1）设定坐标系XYTZ型加工中心结构如图3-6所示，假定机床在初始状态下，在机床床身上创建参考坐标系R，分别在X、Y、Z向工作台，主轴S，刀具T，工件W上创建局部坐标系X、Y、Z、S、T、W，方向与参考坐标系R一致，如图3-6所示。

图3-6 XYTZ型加工中心的坐标系设定

（2）误差运动转换矩阵

1）理想（无误差）状态下各运动轴的转换矩阵。在理想情况下，设X轴工作台移动距离x，Y轴工作台移动距离y，Z轴工作台移动距离z，则坐标系X到坐标系y的齐次变换矩阵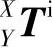、坐标系y到参考坐标系R的齐次坐标变换矩阵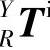，参考坐标系R到坐标系Z的齐次变换矩阵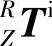分别为

理想状态下主轴和Z轴无相对运动，因此坐标系Z到主轴坐标系S的齐次变换矩阵为单位矩阵，即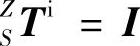;刀具与主轴固连，因此主轴坐标系S到刀具坐标系T的齐次变换矩阵为单位矩阵，即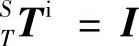；工件与X工作台之间无相对运动，因此T件坐标系W到坐标系X的齐次变换矩阵为单位矩阵，即。

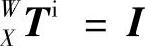在理想情况下，当机床分别沿X、Y、Z方向移动x、y、z距离时，工件坐标系W到刀具坐标系T的变换矩阵为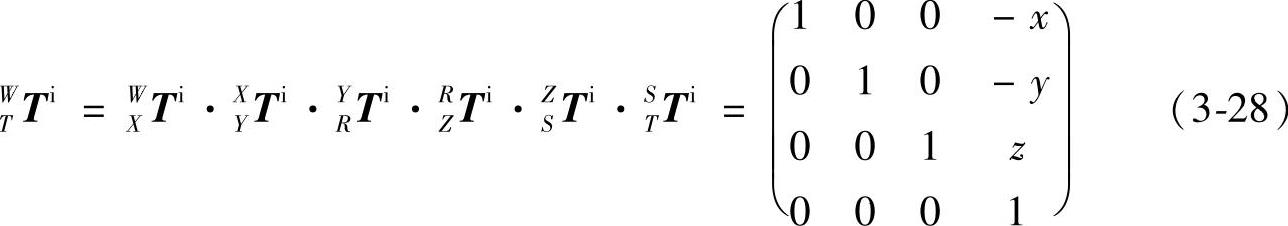(www.xing528.com)

可知在理想情况下，刀具坐标系在工件坐标系中的坐标为（-x，-y，z）。

2)实际状态（有误差）下各运动轴的转换矩阵。在实际情况下，工作台X轴存在三个移动误差δ_xy、δ_yx、δ_zx，三个转角误差ε_xx、ε_yx和ε_zx，则工作台X到工作台Y的变换矩阵为

当工作台Y移动距离y时，由于存在三个移动误差δ_xy、δ_yy和δ_zy，三个转角误差ε_xy、ε_yy、ε_zy，一个垂直度误差S_xy，基于小误差假设，根据齐次坐标变换原理，工作台Y到参考坐标系的变换矩阵为

当Z移动距离z时，由于Z轴移动时存在三个移动误差δ_xz、δ_yz和δ_zz…三个转角误差ε_xz、ε_yz和ε_zz…两个垂直度误差S_xz和S_yz，基于小误差假设，则参考坐标系R到坐标系Z的转换矩阵为

由于实际状态下，刀具与主轴无相对运动，因此主轴坐标系S到刀具坐标系T的齐次变换矩阵为单位矩阵，即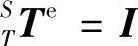；由于数控机床主轴的制造精度较高，由主轴引起的误差较小可忽略不计，因此坐标系Z到主轴坐标系S的齐次变换矩阵为单位矩阵，即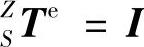；工件与X工作台无相对运动，因此工件坐标系W到坐标系X的齐次变换矩阵为单位矩阵，即。

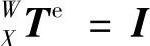在实际状况下，当机床分别沿X、Y、Z方向移动x、y、z距离时，工件坐标系W到刀具坐标系T的变换矩阵为

（3）XYTZ型加工中心综合数学模型 等同TXYZ型加工中心综合数学模型的推导过程，可得XYTZ型加工中心工件坐标系W到刀具坐标系T的误差运动变换矩阵：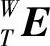

从而可得XYTZ型加工中心综合误差模型：

3.XYZT型加工中心的综合数学模型

（1）设定坐标系XYZT型加工中心结构如图3-7所示，假定机床在初始状态下，在机床床身上创建参考坐标系R，分别在X、Y、Z向工作台，主轴S，刀具T，工件W上创建局部坐标系X、Y、Z、S、T、W，方向与参考坐标系R一致，如图3-7所示。

（2）误差运动转换矩阵

1）理想（无误差）状态下各运动轴的转换矩阵。在理想情况下，设X轴工作台移动距离x，Y轴工作台移动距离y，Z轴工作台移动距离z，则坐标系X到坐标系Y的齐次变换矩阵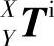、坐标系Y到坐标系Z的齐次坐标变换矩阵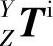，坐标系Z到参考坐标系R的齐次变换矩阵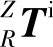分别为

图3-7 XYZT型加工中心的坐标系设定

理想状态下主轴和立柱无相对运动，因此参考坐标系R到主轴坐标系S的齐次变换矩阵为单位矩阵，即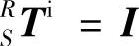；刀具与主轴固连，因此主轴坐标系S到刀具坐标系T的齐次变换矩阵为单位矩阵，即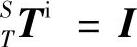；工件与X工作台之间无相对运动，因此工件坐标系W到坐标系X的齐次变换矩阵为单位矩阵，即。

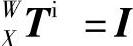在理想情况下，当机床分别沿X、Y、Z方向移动x、y、z距离时，工件坐标系W到刀具坐标系T的变换矩阵为

可知在理想情况下，刀具坐标系在工件坐标系中的坐标为（-x，-y，-z）。

2）实际状态（有误差）下各运动轴的转换矩阵。在实际情况下，工作台X轴存在三个移动误差δ_xx、δ_yx、δ_zx，三个转角误差ε_xx、ε_yx和ε_zx，则工作台X到工作台Y的变换矩阵为

当工作台Y移动距离y时，由于存在三个移动误差δ_xy、δ_yy和δ_zy，三个转角误差ε_xy、ε_yy和ε_zy，一个垂直度误差S_xy，则工作台Y到坐标系Z的变换矩阵为

当Z移动距离z时，由于存在三个移动误差δ_xz、δ_yz和δ_zz，三个转角误差ε_xz、εyz和εzz，两个垂直度误差S_xz和S_yz，基于小误差假设，则坐标系Z到参考坐标系R的转换矩阵为

由于实际状态下，刀具与主轴无相对运动，因此主轴坐标系S到刀具坐标系T的齐次变换矩阵为单位矩阵，即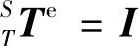；由于数控机床主轴的制造精度较高，由主轴引起的误差较小可忽略不计，因此参考坐标系R到主轴坐标系S的齐次变换矩阵为单位矩阵，即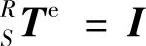；工件与X工作台无相对运动，因此工件坐标系W到坐标系X的齐次变换矩阵为单位矩阵，即。

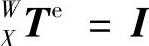在实际状况下，当机床分别沿X、Y、Z方向移动x、y、z距离时，工件坐标系W到刀具坐标系T的变换矩阵为

（3）XYZT型加工中心的综合数学模型 等同TXYZ型加工中心综合数学模型的推导过程，可得XYZT型加工中心工件坐标系W到刀具坐标系T的误差运动变换矩阵：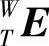

从而可得XYZT型加工中心综合误差模型：