机床热源与温度场优化方案

1.机床热源

机床热源主要可分为两大类：内部热源和外部热源。前者来自切削过程本身，如切削热、运动部件的摩擦热，后者来自切削时的外部条件，如环境温度、阳光、灯光的辐射热等。图2-11所示为机床热源分布图。

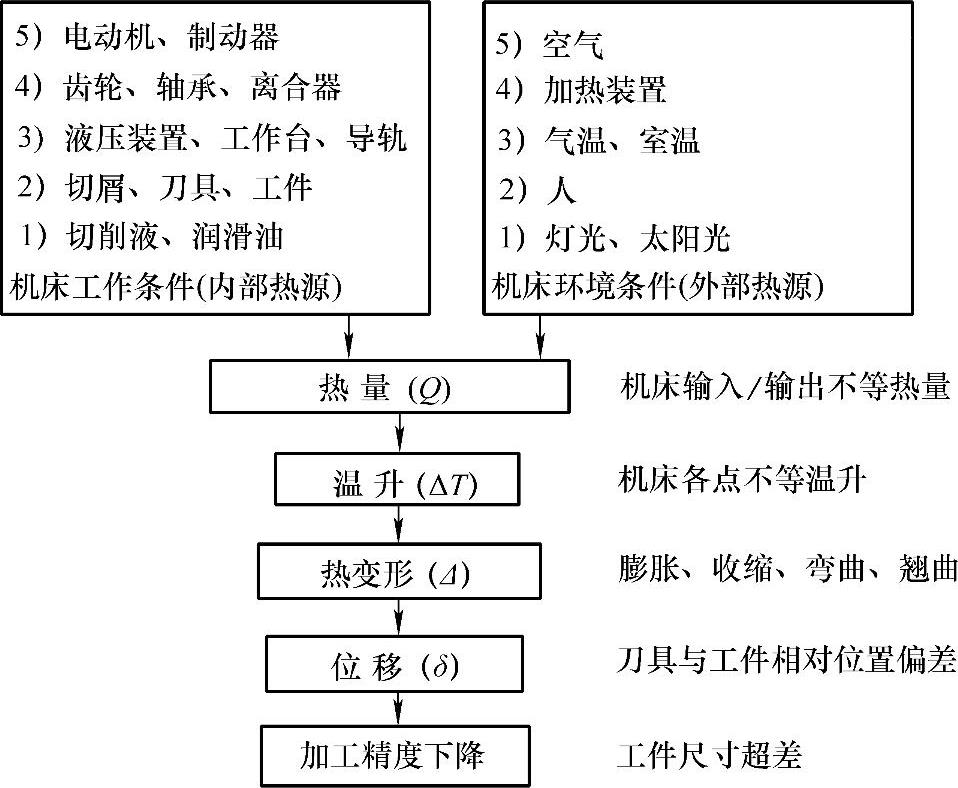
图2-10 机床热变形机理

（1）切削（或磨削）热 在金属切削过程中，由机械能变为被切削材料的变形能，从而产生大量的热量，产生热量的多少将随被切削材料的性质及切削用量的大小而不同。车削时的发热量Q可由式（2-2）确定：

Q=F_zvt （2-2）

式中F_z——切削过程中切削力的垂直分力（N），与被切材料的性质及切削用量有关；

v——切削速度；

t——切削时间；

Q——发热量（J）。

切削所产生的热量主要通过传热分配到工件、刀具和切屑，其分配的百分比与切削速度有关。对于不同加工种类，其切削热的计算与分配各不相同。在车削过程中，大量的热为切屑所带走（速度越高，百分比越高）；传给工件的热量次之，一般在30%以下；而传给刀具的热量又次之，一般不大于5%，高速切削时甚至在1%以下。

对于铣削及刨削加工，传给工件的热量一般在30%以下。对于钻孔和卧式镗孔，因有大量切屑留在孔内，故其传给工件的热量就比车削等高，在钻孔加工中（特别是垂直钻孔中）传给工件的热量往往在50%以上。

至于磨削，因其传给磨屑的热量较少，大部分热量是传给工件的。据试验分析，传给工件的热量通常在总热量的84%左右，传给磨屑的热量仅为4%，传给砂轮的热量约占12%左右。有时工件磨削区域的温度可达800～1000℃，它将使部分工件表面出现烧伤缺陷并使工件产生较大的热变形，从而影响工件的加工精度。

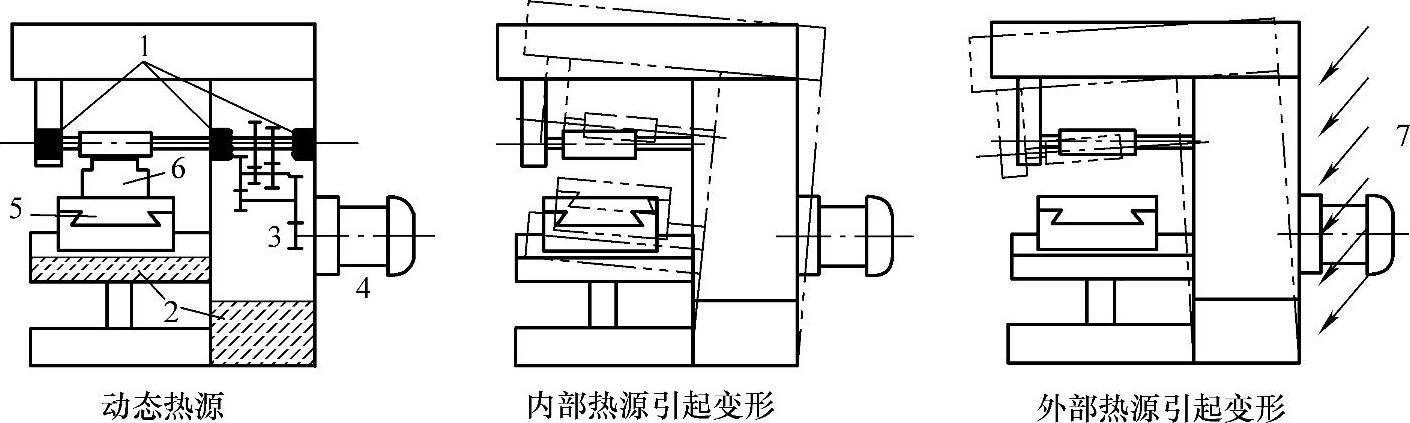
图2-11 机床热源

1—轴承及轴承座 2—切削液及润滑油 3—传动及制动装置 4—泵及电动机 5—导轨 6—切削运动及摩擦 7—外部热源

（2）机床运动副的摩擦热　机床内有各种运动副，如工作台与导轨、摩擦离合器、齿轮传动副、制动器、丝杠与螺母等。它们的运动会产生一定的摩擦力（或摩擦转矩）和摩擦热而形成热源。这些热源使机床部件的温度升高，由于机床各点的温升不同，致使机床产生畸变。

摩擦热的计算一般先计算出运动副摩擦消耗功，然后转化为摩擦热。运动副单位面积消耗的摩擦功率可用式（2-3）计算：

A=fpv （2-3）

式中A——单位面积的功率消耗（W/m²）；

f——摩擦因数；

p——压强（N/m²）；

v——速度（m/s）。

（3）滚动轴承摩擦热的计算 滚动轴承发热量主要是由轴承的摩擦力矩产生，其计算公式为

Q_b=1.047×10^-4nM （2-4）

式中Q_b——轴承单位时间的发热量（kW）；

n——轴承转速（r/min）；

M——轴承摩擦力矩（N·mm）。

轴承摩擦力矩指由轴承滚动摩擦、滑动摩擦和润滑剂摩擦的总和产生的阻滞轴承运转的阻力，可由下式计算：

M=M₀+M₁

式中M₀——与载荷无关的摩擦力矩；

M₁——与载荷有关的摩擦力矩。

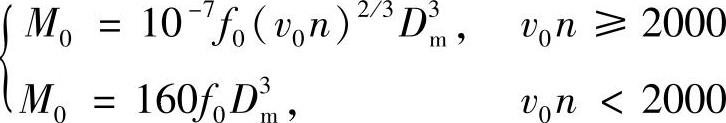
式中f₀——与润滑有关的因数，角接触球轴承脂润滑，单列取f₀=2；

n——轴承转速（r/min）；

v₀——在轴承工作温度下润滑剂的运动粘度（mm²/s）；

D_m——轴承平均直径（mm）。

M₁=f₁P₁D_m

式中f₁——与轴承类型和载荷有关的因数；

P₁——计算轴承摩擦力矩时的轴承载荷（N）。

对于角接触球轴承，有(www.xing528.com)

P₁=0.0013（P₀/C₀）0.33

式中P₀——当量静载荷（N）；

C₀——基本额定定载荷（N）。

P₀=X₀F_r+Y₀F_z

式中X₀——静径向系数，向心球轴承单列公称角为25°时取X₀=0.5；

Y₀——静轴向系数，向心球轴承单列公称角为25°时取Y₀=0.5；

F_r——径向载荷（N）；

F_z——轴向载荷（N）。

2.机床温度场

（1）基本概念

1）机床温度场是在某一瞬间机床上各点的温度分布的总称，温度场是时间和空间位置的函数，在直角坐标系内温度场可表示为

T=T（x，y，z，t）

2）非稳态温度场。物体上各点的温度不仅是坐标位置的函数而且也是时间的函数，物体上这种温度分布随时间而变化的温度场称为非稳态温度场。

3）稳态温度场。物体上各点温度不随时间变化或变化很小，只是坐标位置的函数，物体上这种温度分布称为稳态温度场。

T=T（x，y，z）

4）热平衡状态。单位时间内输入物体的热量与向周围介质散发的热量相等，物体上各点温度保持各自的稳定值，物体处于热平衡状态，各点温度不随时间变化或变化很小，只是坐标位置的函数。

5）热平衡时间是指达到热平衡所需时间。小型机床的热平衡时间一般为2～4h，中型机床的热平衡时间一般为4～6h，大型机床的热平衡时间一般为10～14h。

（2）机床温度场有限元分析 以数控系统为Siemens 840D的XYTZ型三轴加工中心为例。机床参数：最高转速为8000r/min，快速进给速度为33m/min，X、Y、Z轴行程分别为850mm、560mm、650mm。机床切削参数：n=2000r/min，f=0.2mm/r。建立机床有限元模型如图2-12所示。

假定机床初始温度及环境温度为20℃，为模拟一天内机床温度场变化规律，机床首先空运行4h，模拟上午的机床温度变化规律。图2-13所示为机床温度场云图。由图2-13可以看出，4h内机床主轴温度最高为35℃，温升为15℃；丝杠螺母温度其次为26℃，温升为6℃；导轨温度最低为23℃，温升为3℃。

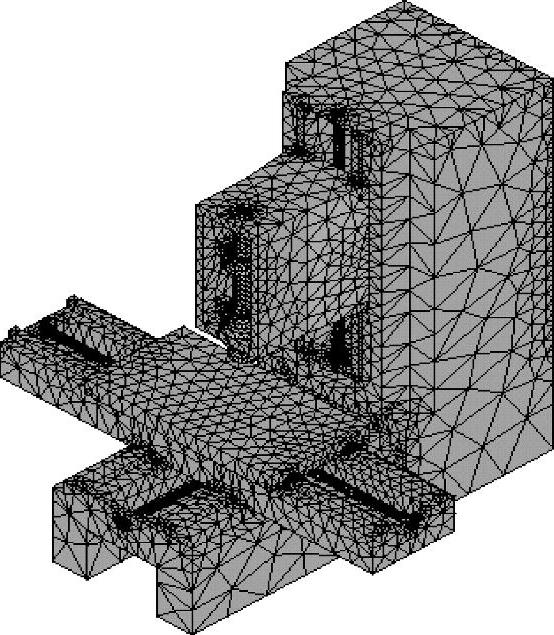
图2-12 机床有限元模型

通过机床温度场分析得出结论：机床在初始运行时温升最大，主轴1000s内温升8℃，随着运行时间的增加逐渐趋于热平衡，在机床运行8000～14400s内的最大温升为1℃，最小温升仅为0.03℃。

由图2-13可以初步确定温度传感器的布置位置，即机床主轴、丝杠螺母和导轨。

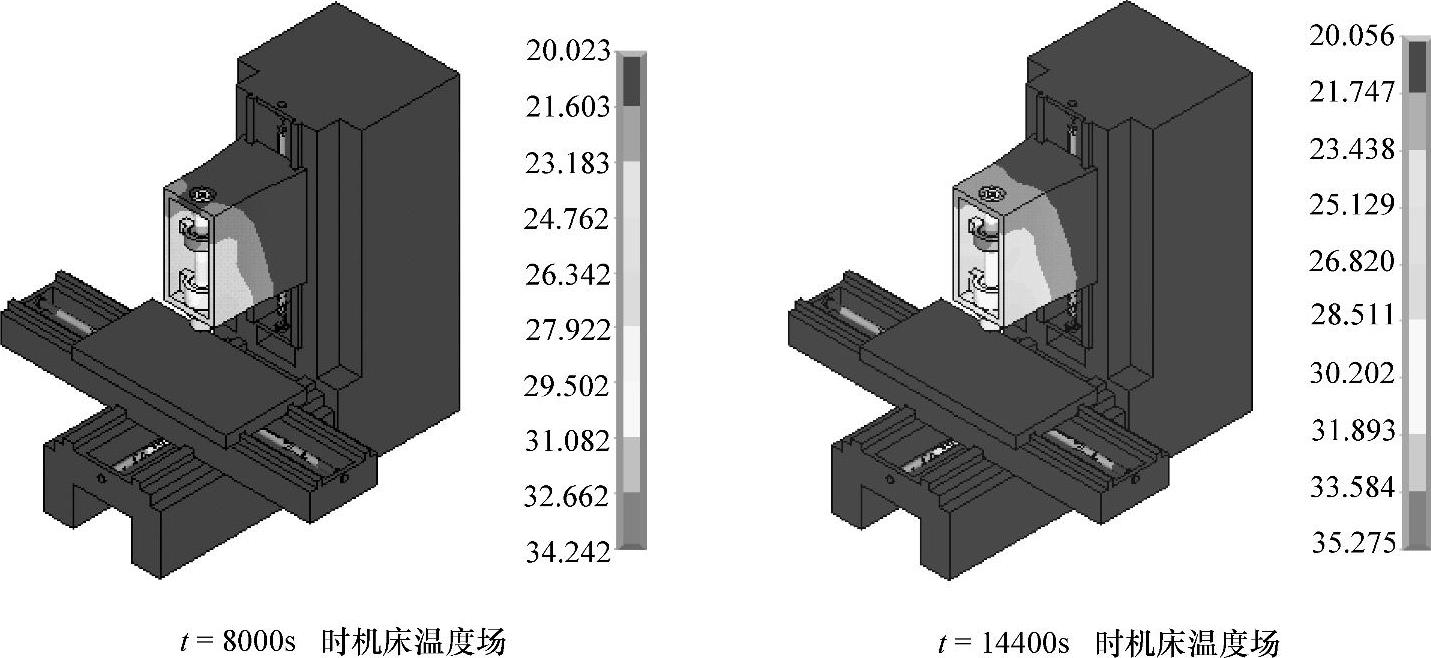
图2-13 机床温度场云图

图2-14所示为主轴、丝杠螺母及导轨温升曲线图。由图2-14可以看出主轴和丝杠螺母达到热平衡时间为8000s；而导轨达到热平衡时间较短，为5000s。机床整机热平衡时间为8000s。

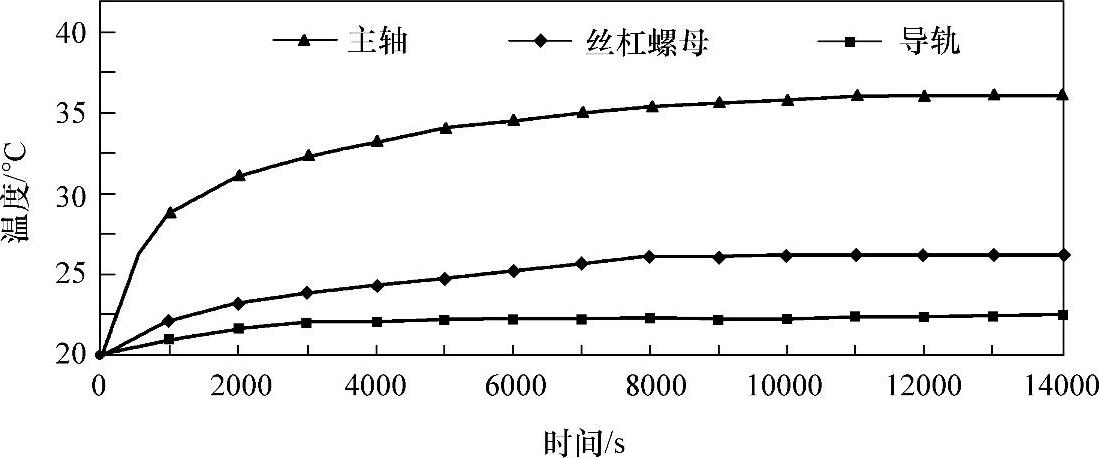
图2-14 主轴、丝杠螺母、导轨温升曲线

为模拟中午休息后继续工作时的机床温度场变化规律，机床停机1h自然冷却，然后继续运行4h，图2-15所示为停机1h及继续运行4h的机床温度场云图。

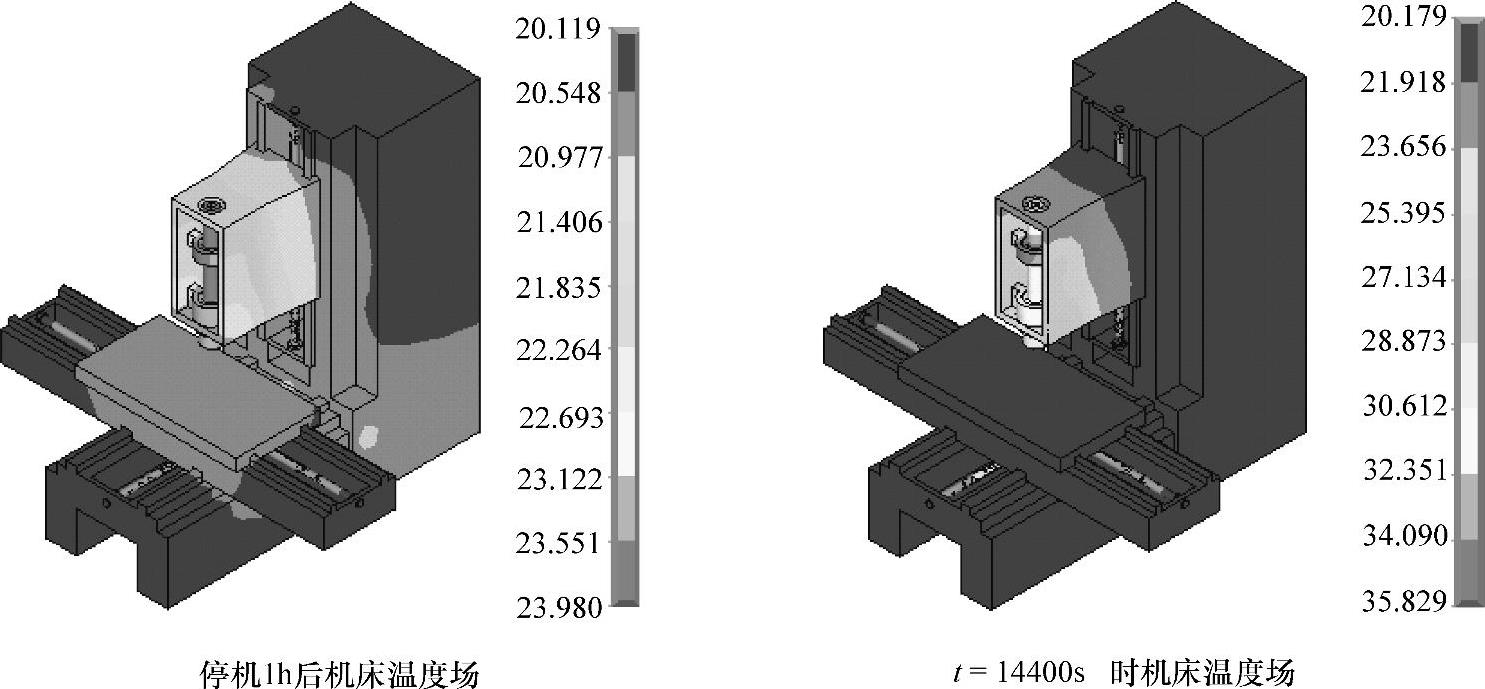
图2-15 停机1h后机床温度场云图

由图2-15可以看出，停机1h后机床的最高温度降为24℃，在主轴位置，机床整机的温度大幅下降。再次运行后机床温度继续升高，温度场变化规律与初始温升4h的变化规律基本相同。

图2-16所示为一个工作日内机床主轴、丝杠及导轨的温度变化曲线图。

由图2-16可以看出，机床一天内的温度变化规律基本一致，即刚起动时机床温升快，随着运行时间的增加，机床逐渐趋于热平衡，这一温度场变化规律为机床热误差建模及测温点的布置提供理论依据。

（3）机床温度场对加工精度的影响

1）机床刚起动时，从冷态开始升温，机床热变形最严重，以后逐渐减少并趋于稳定。在机床起动阶段的热误差也最为严重，使加工精度下降。在精密及超精密加工中经常采用预热机床的方式来使机床达到热平衡或基本热平衡，以避免机床起动阶段热误差对加工精度的影响。为了减少热平衡所需要时间，可在预热中高速运转主轴、高速移动工作台或刀架等。

2）停机后机床温度波动，即温度从升高（或不变）变成降低，当机床再次起动时使加工精度不稳定，该阶段通常发生在换班或休息，为减小该阶段热误差的影响，通常采用不停机的工作方式，即在一天中机床始终处于工作状态，在某些大型工件的加工中，有时甚至连续几天不停机。

3）加工误差与温度变化有关。温度变化大，则加工误差也大。机床温度变化通常与切削用量（主轴转速、进给速度、背吃刀量）、刀具和工件材料等有关。随着切削用量的增加以及被加工材料加工性能的变化，导致机床温升加剧。

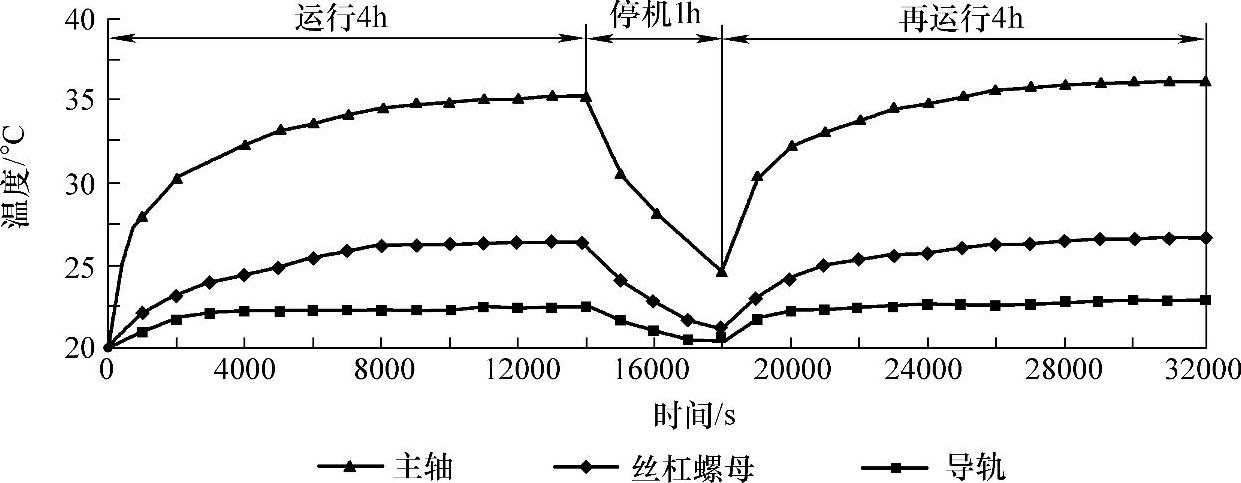
图2-16 一天内主轴、丝杠螺母、导轨温升曲线