集成运放的基本应用：有源滤波器优化

一、实验目的

① 学会用运放、电阻和电容组成有源低通滤波器、高通滤波器、带通滤波器和带阻滤 波器。

② 学习测量有源滤波器的幅频特性。

二、实验原理

本实验是用集成运算放大器和RC网络来组成不同性能的有源滤波电路。

1. 低通滤波器

低通滤波器是指低频信号能通过而高频信号不能通过的滤波器。用一级RC网络组成的低通滤波器称为一阶RC有源低通滤波器。为了改善滤波效果一般都采用两级RC网络，而且为了克服在截止频率附近的通频带范围内幅度下降过多的缺点，通常采用将第一级电容C的接地端改接到输出端的方式。如图1.16.1所示，即为一个典型的二阶有源低通滤波器。

图1.16.1 二阶低通滤波器

其主要性能参数有：

① 通带电压放大倍数：

② 传递函数：

③ 频率特性：

将上式中的s换成jω，并令，可得

当f = f0时，，其幅频特性为

其中：，为截止频率，它是二阶低通频滤波器通频带界限频率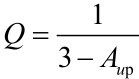；，为品质因数，它的大小影响低通滤波器在截止频率处的幅频特性的形状。

2. 高通滤波器

只要将低通滤波电路中起滤波作用的电阻、电容互换，即可变成有源高通滤波器，如图1.16.2所示。高通滤波器的性能与低通滤波器的相反，其频率响应和低通滤波器的频率响应是“镜像”关系。

图1.16.2 高通滤波器

其主要性能参数有：

① 通带电压放大倍数：

② 传递函数：

③ 频率特性：

将上式中的s换成jω，并令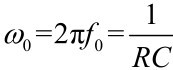，可得

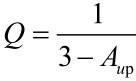令，则可得：

3. 带通滤波器

这种滤波电路的作用是只允许在某个通频带范围内的信号通过，而比通频带下限频率低和比上限频率高的信号都被阻断。将二阶低通滤波电路中的一级改成高通滤波器，即可构成典型的带通滤波器，如图1.16.3所示。

图1.16.3 典型二阶带通滤波器

其主要性能参数有：

① 传递函数：

其中

② 中心频率和通带电压放大倍数：

将上式中的s换成jω，并令，则可得

通带电压放大倍数是

③ 通带截止频率：

④ 通带宽度：

⑤ Q值：

⑥ 频率特性：

这种电路的优点是改变Rf和R4的比例就可改变通带宽度，但不会影响中心频率。

4. 带阻滤波器(www.xing528.com)

如图1.16.4所示，这种电路的性能和带通滤波器相反，即在规定的频带内，信号不能通过（或受到很大衰减），而在其余频率范围，信号则能顺利通过。带阻滤波器常用于抗干扰设备中。

图1.16.4 二阶带阻滤波器

其主要性能参数有：

① 通带电压放大倍数：

② 传递函数：

③ 中心频率：

将上式中的s换成jω，并令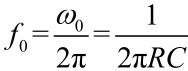，则可得

④ 通带截止频率及阻带宽度：

⑤ Q值：

⑥ 频率特性：

三、实验设备与器件

±12 V直流电源；函数信号发生器；双踪示波器；交流毫伏表；频率计；集成运算放大器μA741×1，电阻、电容若干。

四、实验内容

1．二阶低通滤波器

按图1.16.1连接实验电路。

接通±12 V电源，ui接函数信号发生器，令其输出为1 V的正弦波，改变其频率，并维持ui不变，测量输出电压uo，记入表1.16.1中。

表1.16.1 二阶低通滤波器测试数据

2．二阶高通滤波器

按图1.16.2连接实验电路（ui=1 V的正弦波信号）。

按表1.16.2的内容进行测量，并将结果记入表1.16.2中。

表1.16.2 高通滤波器测试数据

3．带通滤波器

按图1.16.3连接实验电路，其中R = 160 kΩ，R2 =22 kΩ，R3 =12 kΩ，Rf'=R4=47 kΩ，C=0.01 μF时，求出上限频率、中心频率、下限频率、Q和增益。数据表格自拟。

① 实测电路的中心频率f0。

② 以实测中心频率为中心，测出电路的幅频特性。

4．带阻滤波器

按图1.16.4所示的双T型RC网络连接实验电路。数据表格自拟。

① 实测电路的中心频率。

② 测出电路的幅频持性。

五、预习要求

① 复习有源滤波器的内容。

② 分析图1.16.1、图1.16.4所示电路，写出它们的增益特性表达式。

③ 计算图1.16.1、图1.16.2所示电路的截止频率，1.16.3、图1.16.4所示电路的中心频率。

六、实验报告要求

① 整理实验数据，画出各电路实测幅频特性。

② 根据实验曲线，计算截止频率、中心频率、通带或阻带宽度及品质因数。

③ 总结有源滤波电路的特性。