聚类,顾名思义,就是将相似的数据组织在一起,是一种典型的非监督学习算法。聚类过程通过对没有标记的训练样本数据进行学习,自动地将相似的样本划分为同一类,从而反映出数据的内在规律或特性。不同的类别所代表的含义一般需要由使用者进行分析。聚类的演示如图4.34所示。从图中可以很明显地观察到有两类数据,其中实心方形点代表着两个类别的中心。
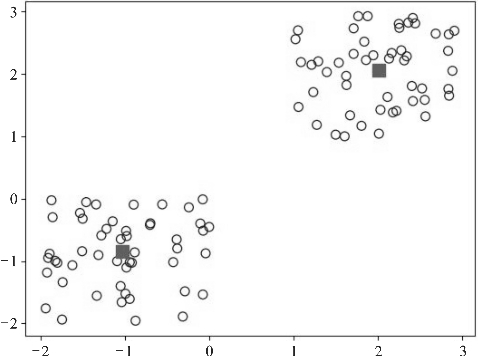
图4.34 聚类的演示
严格来说,聚类和分类是有区别的。分类通常是按照已经确定的模式和判断标准对目标进行划分,也就是说事先已经有了数据划分标准。比如,在监督学习中,通过学习来得到样本属性和分类标准之间的关系,建立分类模型,然后用于对只包含样本属性的数据进行分类。而聚类事先并不知道具体的划分标准,甚至不知道到底有多少类,由算法判断数据之间的相似性,把相似的样本聚集到一起,使之成为有意义的同一类(也称为同一个簇(cluster))。通过聚类使同一类别的数据之间的相似性尽可能大,使不同类别的数据之间的差别尽可能大。
让机器能够将相似的样本划分为同一类,首先要解决的就是相似性度量的问题,而相似性度量通常采用一种距离的测度,比如曼哈顿距离、欧氏距离等,这部分内容在本书4.2.4节中已经进行了重点介绍。常用的聚类方法有k均值(k-means)聚类、基于密度的噪声空间聚类(DBSCAN,density based spatial clustering of applications with noise)、层次聚类(hierarchical clustering)等。
1.k均值聚类
k均值聚类通常需要自行确定类的个数。每一类都有一个中心,也就是质心或均值,如果用其作为该类的代表,则相当于进行矢量量化(VQ,vector quantization)。如图4.35所示,五角星表示学生宿舍的分布,如果希望设置3个学生服务点,能尽量离所有学生近一些,那么就可以考虑将学生宿舍聚类成3个簇,选择3个簇的中心作为设置目标点,如图中的3个方形所示。

图4.35 聚类的应用示例
具体的实现算法如下。
(1)初始化。
根据类的个数k,随机选择k个聚类点作为初始质心。

(2)分配。
计算每个样本数据到k个初始质心的距离,将其分配给距离最近的初始质心所属的类。这样,所有数据就被分成了k个类。
(3)更新。
根据每一类中的点计算该类新的质心,得到k个新质心点。然后返回步骤(2),重新将数据划分为新的k个类,再执行步骤(3)进行更新,不断迭代这个过程,直到新的质心位置基本不变或达到最大迭代次数为止。(完整代码请参考\C4\s4_4_2_Clustering\kmeans01.py。)

k均值聚类算法比较简单,但也存在一些需要注意的问题。
首先是最开始初始化质心时,不同的初始化值会影响到最终的聚类结果。解决办法是:可以进行多次初始化,多次运行聚类算法,取最好的结果。一种改进算法称为Bi-kmeans算法,Bi是binary的缩写,使用该算法结果会稳定许多。该算法将聚类后簇内数据距离该簇中心的误差平方和(SSE,sum of square error)作为评价指标。
Bi-kmeans算法的流程为:
(1)首先将所有数据当作一个类,求出其质心,然后将质心分别乘以略大于1和略小于1的系数,分裂成两个质心,再采用k=2的k均值方式得到两个质心的最终位置后,分别计算总误差。
(2)对每个簇重复之前的步骤,聚类成2个簇,分别计算聚类后SSE减少的值,选取使得SSE减少最多的那个簇进行划分。
(3)重复步骤(2),直到得到k个类后为止。
以图4.36为例进行说明,需要执行k=4的聚类。首先将整体数据集分为簇1和簇2。对簇1和簇2分别进行k=2划分,得到簇1划分后SSE减少8(=30-(12+10)),簇2减少5(=40-(15+20)),所以选择对簇1进一步进行k=2的聚类,得到簇3和簇4。接下来,对当前的3个簇,即簇2、簇3和簇4分别进行k=2的聚类,计算SSE的减少值。簇2在之前的步骤中已经计算过SSE的减少值为5,簇3 SSE的减少值为2(=12-(3+7)),簇4 SSE的减少值为1(=10-(2+7)),所以选择簇2进行k=2的聚类,得到簇5和簇6。所以,最终得到4个类,分别为簇3、簇4、簇5、簇6。
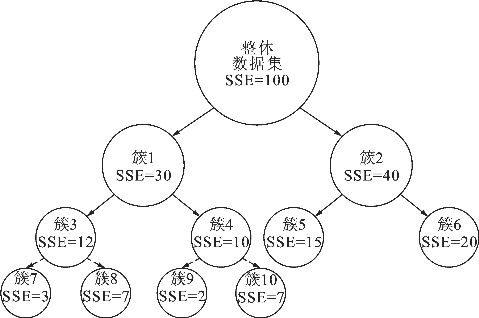
图4.36 Bi-kmeans算法示意图
k均值聚类算法需要注意的第二个问题是k值的选取。有时候并不知道数据应该包含几个不同的类别。通常可采用一些方法来确定k的大小,比如用经验法采用以下公式:
![]() (https://www.xing528.com)
(https://www.xing528.com)
但该方法并不具备代表性,更常用的方法有手肘形状法(elbow method)等。手肘形状法通过绘制簇数量和簇的最大方差或者簇内两个元素的最大距离等参数的曲线图,如图4.37所示,寻找最佳状态点,也就是手肘的弯曲处,将其对应的值作为最佳k值。

图4.37 手肘形状法示意图
使用k均值聚类算法还需要注意的是:它采用简单的相似性度量,对数据的所有特征同等对待,并不关联数据的实际应用环境,所以通常需要更多地关注数据预处理问题。比如,在有些场景下,数据的不同特征之间可能具有不同的权重,所以需要考虑加权处理。再比如,数据的某些特征对于聚类不仅没有任何意义,还会带来干扰,这时就需要予以去除。对于图4.38所示的数据,k均值聚类的效果就不太好,这时可以采用其他的聚类算法,比如基于密度的噪声空间聚类算法。
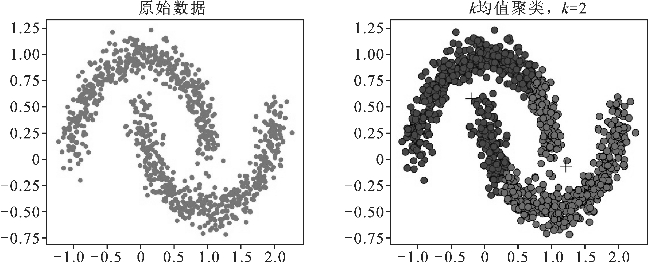
图4.38 非球形分布的k均值聚类效果演示
2.基于密度的噪声空间聚类
基于密度的噪声空间聚类基于密度对数据点进行处理,主要是将特征空间中足够密集的点划分为同一个簇,簇的形状可以是任意的,并且具有较好的抗噪声性能。基于密度的噪声空间聚类的基本思想是如果某个特定数据属于某个簇,那么它和这个簇中的许多其他的点的距离应该都很近。它的工作流程如下。
(1)定义两个参数:一个正的参数ε,表示密度的邻域半径;一个自然数minPoints,表示邻域内的最小点数,称为邻域密度阈值。
(2)标记所有对象为unvisited。
(3)随机选择一个unvisited对象p,标记其为visited。
(4)如果p的ε邻域内包括其自身至少有minPoints个对象,则将这些对象放入集合N中,并且创建一个新的簇C,将p放入其中。
①检查N中所有标记为unvisited的数据对象p',将其标记为visited,并看它们是否在ε邻域内也包含至少minPoints个数据对象,如果是则将这些对象也添加到集合N中。
②如果p'还不是任何簇的成员,则将其添加到簇C中保存。
③以递归的方式扩展簇C,直到C没有可以加入的点,返回到步骤(3)。
(5)否则标记p为噪声,并返回到步骤(3)。
针对图4.38左图采用基于密度的噪声空间聚类算法,选择ε=0.2,minPoints=20时,聚类的结果如图4.39所示。基于密度的噪声空间聚类算法实现代码可参考C4\s4_4_2_Clustering\DBSCAN01.py。
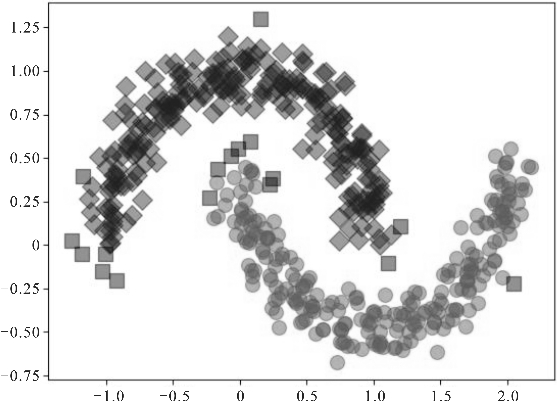
图4.39 基于密度的噪声空间聚类效果演示
图4.40所示为基于密度的噪声空间聚类算法在ε=1.0,min Points=4时的工作流程示意图,其中空心点表示边界点。

图4.40 基于密度的噪声空间聚类算法的工作流程示意图
基于密度的噪声空间聚类算法的运行速度相比k均值聚类算法要慢一些,在应用时不需要提前设置类的个数,但需要提前确定ε和minPoints的值,选择不同的参数值会有不同的聚类结果。同k均值一样,不同的初始值也会影响到聚类,所以在应用该算法时也需要根据情况进行多次尝试。
对于具有不同密度的簇数据,ε参数的选择会比较困难,导致基于密度的噪声空间聚类算法的效果也可能不是很好,这时可以采用OPTICS(ordering points to identify theclustering structure)算法,得到不同邻域参数下的聚类结果。
3.层次聚类
层次聚类可以降低链式效应。所谓链式效应,是指A与B相似,B与C相似,聚类时会将A、B、C聚合为一类,但是如果A与C不相似,则会造成聚类误差。层次化聚类有自顶向下分裂(divisive)和自底向上聚合(aglomerative)两种方法。分裂层次聚类擅长识别大型集群,而聚合层次聚类擅长识别小聚类。这里主要介绍自底向上的聚合层次聚类。
聚合层次聚类初始时,将每个数据样本都作为一个簇,计算距离矩阵,找出矩阵中除对角线以外距离最小的两个簇,将其合并为一个新的簇,更新距离矩阵,也就是删除两个簇对应的行和列,将合并得到的新簇插入矩阵中。然后重复上述过程,直到将数据样本聚合成一个簇。图4.41演示了聚合层次聚类形成的树形图(代码请参考C4\s4_4_2_Clustering\AGNES01.py)。
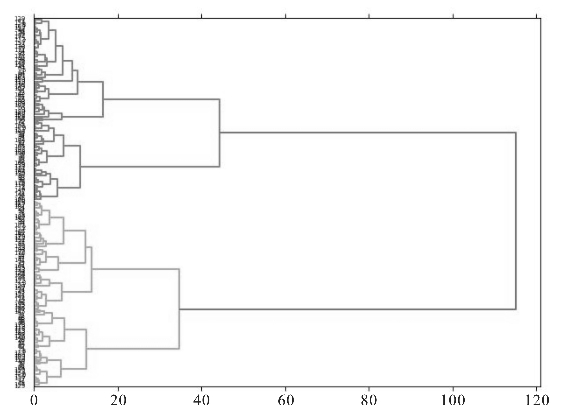
图4.41 聚合层次聚类算法流程演示
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




