人工神经元的概述与应用

人工神经元的结构模仿了生物神经元，最早的结构称为感知机，它可以看作是神经网络的基础。图4.20示意了一个简单的人工神经元的基本结构。它能接收多个输入信号，每个输入信号乘以固定的权重（weight），再加上一个偏置（bias）进行求和，只有当这个总和超过某个界限时，神经元才被激活，并输出一个信号。它的数学模型可表示为：

权重用来控制输入信号的重要程度；偏置用来调节神经元整体信号情况，表示被激活的容易程度；函数φ称为激活函数（activation function），用来控制是否被激活以及输出。从数学表达式上来看，权重参数和偏置参数可以统称为权重。

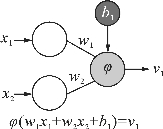
图4.20　人工神经元的基本结构示意

最早的感知机模拟神经元的激活机制，激活函数使用的是阶跃函数，当超过某个阈值时输出为1，否则输出为0。它因为无法进行非线性分类，输出只有1和0两个值，不能用于反馈调节的过程，所以现在基本不会使用了。

现在使用的激活函数目的有两个：一是给神经元引入非线性元素，使得神经网络可以逼近任何非线性函数，从而应用到众多的非线性模型中；二是应对进一步处理过程中遇到的各种计算问题，比如求导等。

常用的激活函数有以下一些（实现代码请参考本书C4\s4_3_2_ActivationFunction）。

（1）sigmoid函数。

其导数为：

函数及其导数的图形如图4.21所示。

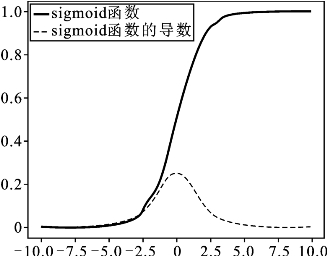
图4.21　sigmoid函数及其导数的图形

sigmoid函数的特点是：输出在0到1之间，这个和概率的范围是一致的；常用于二分类任务的最后一级。它的主要缺点有三个。一是计算量大。二是用于反向传播算法中计算梯度时，容易出现梯度消失情况。从图4.21可以看到，当输入较小或者较大时，导数都是接近于0的。三是输出值只有正值，输出会出现偏移，导致收敛效果不好，出现zigzag现象。

（2）tanh（双曲正切）函数。

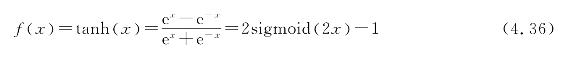
其导数为：

f＇（x）=1-f2（x）　（4.37）

函数及其导数的图形如图4.22所示。

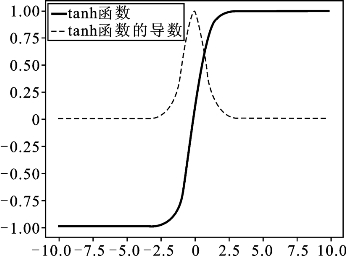
图4.22　tanh函数及其导数的图形

tanh函数的特点是：将任意实数映射至±1之间，相当于均值为0。由图可以看到它和sigmoid函数很相似，都是S形状的函数。通常在神经网络的中间层使用tanh函数会比用sigmoid函数要好一点，可以加快收敛速度，减少迭代次数，但是仍然会出现梯度消失现象。

（3）ReLU（rectified linear unit）函数。

f（x）=max（0，x）　（4.38）

其导数在x大于0时为1。

函数及其导数的图形如图4.23所示。

图4.23　ReLU函数及其导数的图形

ReLU函数的优点是：计算简单，在梯度下降算法中收敛速度比tanh函数和sigmoid函数快很多。缺点是：在用于神经网络的训练时，神经元容易出现不对任何数据有激活现象的情况，梯度始终为0，这样的神经元被称为“die”，即死亡结点；和sigmoid函数一样，输出有偏移现象，输出均值大于0。

针对Re LU函数的一些不足，人们提出了一些改进的Re LU函数，比如leaky Re LU函数、PReLU函数、ELU函数等，如图4.24所示。

(www.xing528.com)

图4.24　一些改进的ReLU函数

leaky Re LU/PRe LU的函数公式为

f（x）=max（ax　，x）　（4.39）

其中，当a等于一个固定的较小的`常数时，比如0.01，就称为Leaky ReLU函数；如果a不是固定的，而是可学习的，就是PRe LU函数。如果不同神经元使用的a不同，是一个在较小范围内的随机值，则称为randomized leaky Re LU函数。如果将小于0的部分限制在某一个较小范围之内，使其处于软饱和状态，就成了ELU函数：

（4）maxout函数。

maxout函数是2013年由Goodfellow提出来的。它也是一种可学习的激活函数。是可变的，它将神经元的输入加权和进行了加权。它是一个分段线性函数，取k个直线中值最大的直线所在的那一段，如图4.25所示，相当于用分段线性函数拟合任意凸函数，所以它具有很强的拟合能力。k值越大，分段越多。图4.25分别拟合了Re LU函数、绝对值函数、二次函数。它的缺点就是参数将会成k倍增加，本来只需要一组参数，现在需要k组参数。

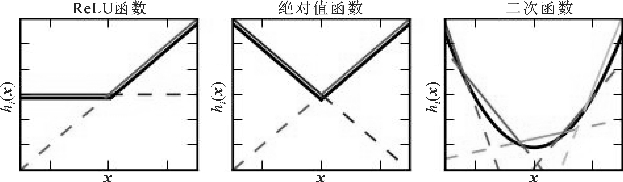
图4.25　maxout函数示意

（5）softmax函数。

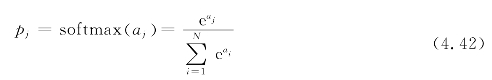
softmax函数又叫归一化指数函数。它可以把一个序列［a1，a2，…，aN］变成类似概率的输出［p1，p2，…，pN］。经过该运算之后，所有pj的值都在［0，1］范围内，并且所有的pj加在一起等于1，所以它常在解决多分类问题的神经网络的输出层使用。

例4.6　计算序列［1，2，3］经过softmax函数后的输出。

解　直接代入式（4.42），有

同理可得到softmax（a2）、softmax（a3），最终输出结果为［0.090 030 57，0.244 728 47，0.665 240 96］。

在应用softmax函数时需要注意一些问题。比如，如果例4.6的输入序列为［1001，1002，1003］，分子和分母的数值都会变得非常大，比如分子将变成e1001，而计算机存储的数据位宽一般都有限制，会出现数值过大溢出问题。所以，通常该函数分子和分母同时乘以一个系数，最后变为

其中，D可以取任意值，一般取序列中最大值的负数。

经过以上处理，虽然可以解决数值很大的问题，但如果序列值相差过大，比如［-10 000，0，10 000］，依然会出现溢出问题，有时提示NaN（not a number）问题，这时可以考虑取对数，即采用logsoftmax函数：

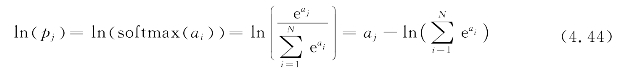
它还省去了一个除法和指数计算，数值也更稳定。

softmax函数的偏导数（梯度）为

进一步化简，分为以下两种情况：

当j=i时

当j≠i时

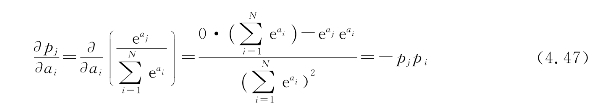
如果将softmax函数与交叉熵损失函数相配合，则梯度计算将会变得非常简单。这将在下一节进行介绍。

还有许多其他激活函数，这里不一一列举。激活函数主要是为人工神经元加入非线性因素，提高其表达能力，以及解决神经网络在完成不同任务要求时、在不同场景的计算情况下遇到的问题而提出的。单个神经元的功能比较有限，组成多层的神经网络才能有更强大的功能。