支持向量机算法详解

支持向量机在本质上是用于对象分类的一种手段。它由模式识别中广义肖像算法（generalized portrait algorithm）发展而来，并成了统计学习理论的一部分。1995年Cortes和Vapnik首次提出了软边距的非线性支持向量机并用于手写字符识别。它在手写字符识别方面表现出了较好的性能，一度成为机器学习的主流技术，直到现在被深度学习取代。

虽然，现在深度学习技术在人工智能领域一枝独秀，但是，在样本数量少、数据特征维度较高的场景下，支持向量机依然有着不可替代的优势。

支持向量机是一种监督学习方法，首先需要用一组标记好了的训练数据进行训练，支持向量机训练算法通过寻求结构风险最小（structural risk minimization）来提高学习机泛化能力，实现经验风险（empirical risk）和置信风险（VC置信范围）同时最小化。

经验风险是指训练好的分类器对训练数据分类得到的误差，用Remp（α）表示。置信风险是指分类器对未知样本进行分类得到的误差，用Φ（h/l）表示，其中h是VC维度（vapnik chervonenkis dimension），l是样本数。在一般情况下，VC维度越高，机器学习的置信风险也就越高，泛化能力就会越差。当然，也存在相反情况，比如k-NN算法在k=1只有一个类时，VC维度无限，经验风险为零，泛化能力也无限。所以，通常置信风险越小意味着模型的泛化能力越强。结构风险最小化就是追求Remp（α）+Φ（h/l）最小化。

VC维度可以理解为某假设空间能打散（shatter）的最大数据集的大小。如果将N个样本点分为2类，则每个点可以有2种分法，总共就有2N种分法，也可以理解为有2N个学习问题。如果存在一个假设空间H，该空间能准确无误地将最多N个样本点的2N种不同分类方法都划分出来，那么就称空间H的VC维度为N。

比如由直线构成的线性空间或称二维空间的超平面（hyperplane），或二维平面的线性分类器，可以将二维平面中的3个点的8种组合都划分出来，如图4.15所示。但如果是4个点，其16种组合中就存在无法划分的情况，如图4.16所示。所谓超平面，可以理解为n维线性空间中维度为n-1的子空间，比如二维平面中的直线。

图4.15　直线可以将平面中3个点的各种组合都分散出来

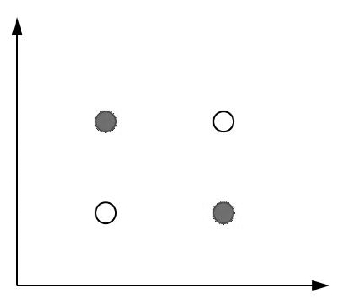
图4.16　直线无法分散平面中4个点中的一种组合

通常来讲，k维空间的超平面H的VC维度VC（H）=k+1，比如三维空间里的平面的VC维度就是4。

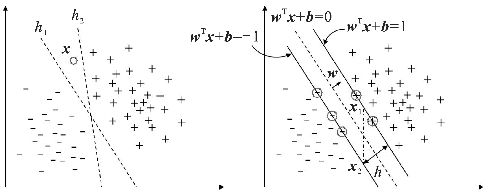
图4.17用了更直观的方式演示什么是更好的分类器。图中训练样本被分成了标记为+、-的两个类，左图中的h1、h2是两个超平面，也就是两个分类器，用于将样本区分开来。超平面可以用分类函数f（x）=wTx+b表示，h1和h2就对应着不同的wT和x参数。显然，h1的性能看着比h2的性能好。对于图中的未知数据x点，h1将其归入+类，而h2则会将其归入-类。支持向量机的目的就是找到这个最适合把两类数据分开的超平面，也就是图中的h1。怎么找呢？就是找两边的数据离这个超平面间隔最大的那个超平面。一个点离这个超平面距离（间隔）越大，分类的置信度（confidence）就越大。

(www.xing528.com)

图4.17　支持向量机的基本原理

包含N个样本点的数据集到超平面的间隔可以定义为所有样本点中到这个超平面间隔最小的那个值，而支持向量机就是要使这个间隔值达到最大，这就是支持向量机算法的基础，即最大间隔（max-margin）准则。对于图4.17中的右图，假设使这个间隔最大的超平面wTx+b=0已经找到，f（x）=wTx+b就可以看作是x到超平面的距离。显然，+类和-类到超平面的距离相等，为了便于计算，令它们的距离分别为+1和-1，也就是样本集中到超平面的最小距离，即图中的两条实线所示，也是分类器的间隔边界，此时h的值就等于2。位于间隔边界上的点就称为支持向量（support vector）（图中用圆标记出来的点）。由于等比例缩放x的长度和b的值时，超平面不会变化，但是f（x）值会变化，因此用几何间隔|f（x）|/||w||代替函数间隔|f（x）|，其中||w||为垂直于超平面向量w的L2-范数。因此，支持向量机的优化目标就变成了最大化1/‖w‖。

由于求1/‖w‖的最大值相当于求‖w‖2/2的最小值，因此支持向量机的目标函数等价于

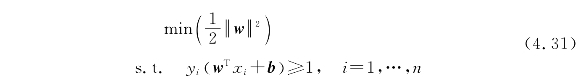
其中，s.t.（subject to）表示约束条件，yi表示分类值，为±1，和它相乘后wTx+b就都是大于或等于1的正值了。

以上所介绍的是支持向量机的基本原理，并假设训练样本数据是线性可分的。在实际分类任务中，很多数据本身在原始的样本空间中是线性不可分的，比如图4.16中的两类数据。解决这个问题的一种重要的方法叫作核函数法。支持向量机通过选择一个核函数K（），将数据映射到高维空间，使其在高维空间变得线性可分，如图4.18所示。核函数能事先在低维上进行计算，并将实质上的分类效果表现在高维上，避免了直接在高维空间的复杂计算，比如径向基核函数（RBF，radial basis function）

可以把原始特征映射到无穷维空间。

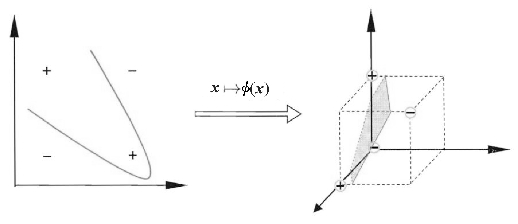
图4.18　通过核函数将线性不可分映射到高维空间

假设低维向量＜w，x＞映射到高维空间变成＜w＇，x＇＞后，能用线性函数f（x´）=wTx´+b分类，那么通过核函数g（x）=K（w，x）+b，直接输入低维向量＜w，x＞，就能得到和f（x＇）相同的结果，而不用去关心具体的映射过程。

常见的核函数有线性核函数、多项式核函数、高斯径向基函数等，不同的支持向量机算法使用不同的核函数。对于核函数的选择，目前还缺少具体的方法，通常只能通过实验观察结果，某些问题可能用某些核函数效果会很好，而用另一些效果就很差，不过，一般用径向基核函数相对来说结果不会出太大的偏差。在4.5节中将介绍在Python中应用支持向量机的方法，而关于支持向量机底层代码的实现算法，最著名的是由John C.Platt于1998年提出的SMO算法。

支持向量机的不足之处主要是当数据的维度比数据样本数大许多时，核函数和正则化项的选择对于避免过拟合非常重要。另外，支持向量机没有直接提供概率估计值，而是通过5折交叉验证来计算。