k最近邻(k-NN,k nearest neighbor)算法最早由Cover和Hart于1968年提出,是机器学习中较简单也比较成熟的算法之一。它的思路非常直观,如果已知有n个被正确分类的样本,那么对于新样本进行预测分类,就看一下和新样本最相似的k个样本大多数属于哪一个类别,相应地认为该新样本也属于这个类别。相似程度的判断可以通过比较样本在特征空间中的距离来实现,也就是查找n个样本中距离新样本最近的k个样本。
简单来说,就是对于一个需要预测的输入矢量x,在已经有分类标签的训练数据集中寻找k个与矢量x最近的矢量的集合,然后把x的类别预测为这k个矢量中数量最多的数据所在那一类别。
比如,在图4.5所示的数据中,每个数据有两个特征x、y,并标上了绿色(方形)和红色(菱形)两类标签,它们属于训练数据集。两个没有颜色的数据(倒三角形)是需要预测的数据。那么,凭直觉可以将左边的倒三角形归入绿色(方形)类,将右边的倒三角形归入红色(菱形)类。这里的直觉其实用到了视觉上的距离,左边数据附近的大多都是绿色(方形),右边数据附近都是红色(菱形)。这就是k-NN算法的基本思想。
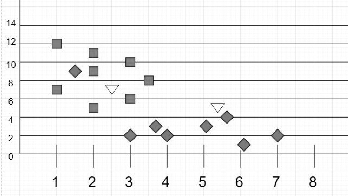
图4.5 分类数据示例
由此,得到k-NN算法的基本过程如下。
(1)将训练的m个数据存入列表train[]。
(2)fori in range(m):
计算待预测数据p与训练数据的距离dist(train[i],p)。
(3)将距离最小的k个数据构成S集合。
(4)返回S中大多数数据所具有的标签。
下面以鸢尾花数据集为例,介绍k-NN算法的基本实现和应用方法。
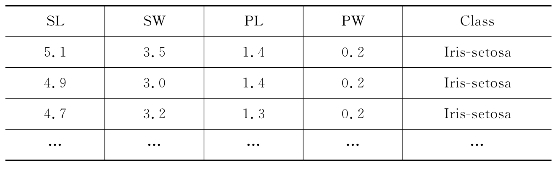
例4.3 经整理过的鸢尾花数据集存储在本书所附文件/p4_3_k NN/data1.txt中,第一行为表头标签名,即SL(sepal length,花萼长度)、SW(sepal width,花萼宽度)、PL(petal length,花瓣长度)、PW(petal width,花瓣宽度)、Class(鸢尾花类别),第2到151行为测量的150条数据尺寸,单位为cm。部分数据如表4.3所示。请用k-NN算法判断SL为5.0 cm、SW为2.9 cm、PL为1.0 cm、PW为0.2 cm的鸢尾花属于什么类型,并评价你有多大把握让人相信你的结论。
表4.3 鸢尾花数据集部分数据
解 依照k-NN算法的基本流程,实现其主要功能模块,相关代码及说明如下。
k-NN算法首先需要解决样本间距离的测量问题,如果采用欧氏距离,也就是求各分量差值的平方和再开方,则需要用到包含各种基本数学函数的math库,代码如下:
 (https://www.xing528.com)
(https://www.xing528.com)

接下来,需要计算待预测的数据和数据集中每一个数据的距离,将距离最近的k个数据找出来。我们可以建立一个大小为k的列表,只往其中加入数据集中距离最小的k个元素及其分类。代码如下:

一旦获得了k个距离最近的数据及其类别列表,就需要编写函数统计其中有哪些类别,以及每个类别中数据的个数,所以考虑使用字典保存,将类别作为键值key,统计的个数作为其值value。


最后,将最大值作为预测结果输出即可:

本例预测结果为:Iris-setosa,预测准确率约为96%。
完整代码参见\p4_3_k NN\k NN_01.py,其中还包括了对模型的评估部分,也就是例4.3的第二问。那么,究竟该怎么评估预测结果的好坏呢?参考代码给出的是一种叫作K折交叉验证(K-fold cross validation)的方式,基本思路就是取数据集中的一部分数据进行训练,将另一部分数据用于测试,这样就可以根据测试结果的正确率来了解模型的大致性能了。关于机器学习模型验证与评估的一些方法,将在下一小节详细说明。
进一步分析可以发现,k-NN算法中,k取得越大,分类的边界会越平滑,但容易出现欠拟合;k取值太小,容易导致过拟合。同样,训练的样本数越大,分类的准确度也会越高。另外,通常把k设置为便于找到多数邻居标签的数量,比如预测属于两类中某一类时,把k设置为奇数更方便。k通常取不大于20的整数。
k-NN算法不但可以应用于分类问题,也可以用于回归问题。在回归问题中,比如有一系列样本坐标(x,y),可以当作训练数据,输入为x,输出y就是标签,当给定一个测试点坐标x1时,预测其坐标y1,采用k-NN算法就是找到k个离x1距离最近的已知样本坐标,对这k个样本的y值求平均,并作为y1的值。如图4.6所示,已知10个点的坐标,预测点x_new=7.6的纵坐标y_new,用k-NN算法进行回归预测,取k=3,在x轴上找到距离x_new距离最近的3个点,如图所示,将这3个点的纵坐标进行平均就得到y_new=129.3。(代码参见/p4_3_k NN/k NN_02.py。)
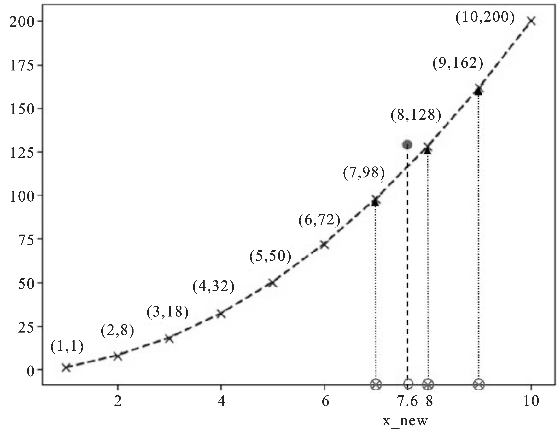
图4.6 k-NN算法回归示例
k-NN算法属于非参数统计方法,也是懒惰学习算法的代表。所谓懒惰学习,是指事先没有分类器,没有训练阶段,收到测试样本后再进行处理。尽管k-NN算法比较简单,但是应用领域还是非常广泛的,包括文本分类、语音识别、图像识别等。比如Indu Saini等人使用k-NN算法进行心电图(ECG)复合波检测,将心电信号的梯度向量作为特征,以CSE MA1_001数据库和MIT-BIH No.100数据库作为训练数据,取k=3,采用欧氏距离取得了较好的效果。
k-NN算法应用中的主要问题就是如何解释模型以及如何理解模型分析的输出。k-NN算法本身与参数无关,对于数据模型,究竟该选哪些参数,哪些参数更能影响输出的结果,这些内容的确定是很重要的。另外,相似性度量本身也有着许多的方法,选用不同的方法会对输出结果有不同的影响。比如在鸢尾花数据集的例子中,4个特征数据范围差别不太大,而且性质相似,具有相同的单位,所以未做任何数据预处理直接采用欧氏距离就能有较好的效果,但是在其他应用场景中,如何去计算距离也是必须考虑的问题。
另外,当数据规模很大时,k-NN算法需要在大量的数据中查找离输入样本最近的k个近邻,这时查找的效率会变得比较重要。那么,如何提高查找效率呢?和数据库一样,建立数据索引。一种索引方法是建立树结构的索引,称为索引树,其基本思想是对搜索空间进行层次划分,根据划分的空间是否有交叠可以分为clipping和overlapping两种。前者划分的空间没有重叠,其代表就是KD树(K-dimension tree);后者划分的空间相互有交叠,其代表为R树(R-tree)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




