动态规划：解决子问题重叠性质、最优子结构性质的问题

动态规划（DP，dynamic programming）由美国数学家Richard Bellman于1956年提出，用来研究多阶段决策过程的优化问题，在数学、计算机、经济学等领域被广泛使用。它也是先将复杂问题分解成简单问题，然后加以解决，核心是在大问题的解决方案中不断地记录和重用已被解决的子问题的解决方案。为了重用子问题的解决方案，它采用了子问题缓存技术，一旦某个给定子问题的解已经算出，就将其记忆化存储，下次再需要计算相同问题时，直接在存储的内容中通过查表获取，每个子问题只计算一次，避免了子问题被大量地重复计算，所以它有时也被称为记录部分子目标解决方案。因为它可以解决一些算法中的重复计算问题，所以在人工智能一些算法的优化上，也经常会采用它。

动态规划有时也称前向后向（forward backward）算法；当使用概率时，称为维特比算法（Viterbi algorithm），这在后面的学习中也会遇到。

动态规划适用于有子问题重叠性质、最优子结构性质且无后效性的问题。子问题重叠性质是指子问题递归分解时并不只出现新问题，有些子问题会重复出现。最优子结构是指问题的最优解所包含的子问题的解也是最优解。无后效性是指分解过程中出现的某个状态一旦确定，将来的过程不会影响到该状态。依据这些性质，我们可以得到采用动态规划求解问题的基本思路如下。

（1）寻找问题的分解方法。一般从问题的结果出发，反向思考问题是什么、子问题又是什么。分解后的子问题应该是有次序的。

（2）考虑存储的问题，确定子问题中会重复计算的状态变量以及存储方法，要求满足无后效性条件。

（3）找出初始条件和边界等限制情况。

（4）分析状态的变化情况，写出状态转移方程，确定好状态变量的计算顺序，比如从前开始往后计算。

下面通过几个例子来学习一下动态规划的思想。

例3.7　编程实现斐波那契（Fibonacci）数列（0，1，1，2，3，5，8，13，21，34，55，…）的计算函数，也就是：

f（0）=0，　f（1）=1，　f（n）=f（n-1）+f（n-2），　n≥2，　n∈N　（3.2）

解　首先用常用的递归方式编程实现该函数，代码如下：

这是最佳实现方式吗？可以看一下递归的计算过程。为了简化，用函数f（n）代替fibo_1（n），假设需要计算f（10），则需要计算f（9）和f（8），而此时f（9）、f（8）的值还未知，只能放入内存里继续递归计算f（9）和f（8），依此类推，图3.25显示了具体计算展开过程。

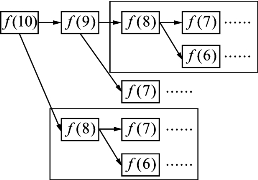
图3.25　递归计算过程中的大量重复

从图中可以看到有大量的计算是重复的，效率不高，怎么解决？由于之前计算的结果后面还会用到，如果把之前计算的结果都保存起来，按照一定的规律推算后面的结果时，就可以通过在数列中重用子数列来提升效率。代码重新编写如下：

此时，时间复杂度和空间复杂度都变成了O（n），大大提高了效率。

接着分析。由于只需要求解第n项的值，而第n项只需要记住前两项的值就行了，因此还能进一步优化，降低空间复杂度。这里，用动态规划的思想来思考，问题是求f（n），子问题为求f（n-1）和f（n-2）。函数重写为：

大家可以对这3个不同的实现方法用Python的time.time（）统计一下函数的运行时间，做一下对比。

有很多的经典问题都是用动态规划的思想实现求解的，比如青蛙过河问题。

例3.8　一只小青蛙要通过河里的石头过河，它一次可以往前跳1级石头，也可以往前跳2级石头，求该青蛙跳到第n级石头上，总共有多少种跳法？

解　首先看一下问题的分解方法，很容易分析出跳到第1级石头上，只有1种方法；跳到第2级石头上，有2种方法，一级一级跳或者一次跳2级。跳到第3级或第3级以上石头上，如果企图用排列组合的方式去推算，那就会有点麻烦了。这时，按照动态规划的思想反过来想，就会容易很多。

计算青蛙跳到第n级石头上的方法时，假设青蛙只可能通过跳1级到这里，或者跳2级到这里。如果它是跳1级过来的，也就说明之前跳到了n-1级；如果它是跳2级过来的，说明之前它跳到了n-2级，所以跳到第n级的总方法数f（n）=f（n-1）+f（n-2）。这个就好像和斐波那契数列的公式一样了，只是初始条件有点不同，f（1）=1，f（2）=2，接下来编程实现就比较容易了。

例3.9　硬币问题：假设你手上有2分、5分、7分硬币各若干，请问如何用最少的硬币数组合出32分钱。

解　用动态规划的方式来思考，看能不能转化为子问题。首先分析最后一步。假如用的最后一枚硬币是第k枚硬币，它只会是2分、5分或7分，那么倒数第2步就变成了用最少的硬币拼出30分（32分-2分）、27分（32分-5分）或25分（32分-7分）。

也就是转成了3个子问题，如何用最少的硬币拼出30分、27分、25分出来，这3种情况中最少的硬币枚数加1就是拼出32分钱的最少硬币数。(www.xing528.com)

用k代表第k枚硬币，x代表需要拼的钱数，用f（x）代表最少硬币数，为了方便保存，把f［x］当作状态。现在问题就变成了f［x］=min（f［x-2］+1，f［x-5］+1，f［x-7］+1）。

初始状态f［0］=0，是拼不出来的状态，并定义f［x＜0］=+∞或-1，最后在计算顺序上，还需要考虑利用之前计算过的结果。

例3.10　背包问题（knapsack problem）：一种组合优化的NP完全（NPC，nondeterministic polynomial complete）问题，给定一组物品，假设数量为N，每件物品质量为wi，价值为vi，如果现在有个背包，最大可以装载的质量为C，请问此时最多能装的价值是多少？假设每种物品最多只能选1个。此时该问题又称为0-1背包问题。

解　任务要求是根据背包容量和可选的物品找到价值最大的组合。定义函数KS（i，j）代表当前背包剩余容量为j时，前i个物品能获得的最大价值。先来看最后一步，看能否分解出子问题。假设最后准备放第i个物品（wi，vi），那么放入前i-1个物品后剩余空间为j时，就存在以下两种可能。

（1）背包剩余空间装不下第i个物品，此时KS（i，j）=KS（i-1，j）。

（2）背包剩余容量可以装下该物品，此时当前的最佳组合方案就只有采用以下两种方式得到：不装该物品得到最大价值，即KS（i-1，j）；装了该物品得到最大价值，即KS（i-1，jwi）+vi。从两者中选较大的那个。因此得到递推关系如下：

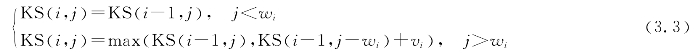
需要重复计算的变量就是KS（i，j）。

考虑初始条件和边界条件，当可以放入背包的物品数为0，或者背包容量为0时，能得到的最大价值也为0。

最后，计算从放入第1件物品开始，考虑背包的容量情况，然后递增1件物品，再计算背包的容量情况，直到最后满足问题要求。

下面通过一个实例说明动态规划的具体计算过程，表3.1所示为物品质量及价值表，假设背包容量最大为12 kg，计算能装入背包的最大价值。

表3.1　物品质量及价值表

具体计算过程列在图3.26中。图中“v”表示价值，“w”表示质量，按照动态规划的思想，从初始条件开始计算，第1行放入物品个数为0时，无论背包的容量是多少，最大价值都是0。接着计算第2行，有1个候选物品，质量为3 kg，价值为3，从左往右，当背包容量大于或等于3 kg时，代入式（3.3）计算，得到能够获得的最大价值是3。依次从上往下，从左往右，编程时通过循环来实现，一直计算到最右下角，即背包容量C=12 kg时，能够装入的最大价值为16。

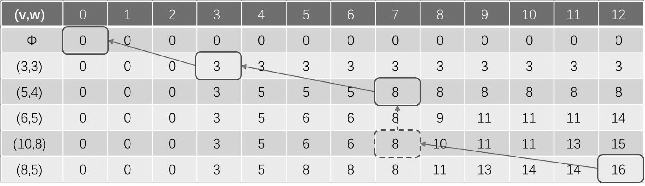
图3.26　动态规划0-1背包问题计算过程说明

再来看一下分解出的子问题，右下角其实就是考察背包的容量为12 kg、物品为5个的情况下的最大价值。它的上面一项15表示背包的容量为12 kg时，只有前4个物品可放入时的最大价值。第5个物品质量为5 kg，价值为8，显然背包的容量为12 kg时，它也是有可能被放入的。如果把它放入后得到的最大价值比15要大，那么肯定会选择放入它的方案。在放入它之前，背包的容量为12 kg-5 kg=7 kg，而背包的容量为7 kg时，前4个物品的最大价值已经在前面的计算过程中得到了，即为8，如图中虚线框所示，加上第5个物品后，价值为8+8=16，大于不考虑它时的15，所以此处得到的值为两者之间较大的值，即16。

得到最大价值后，通过回溯就能找到将物品装入背包的方案，如图中箭头所指。从右下角16开始，如果向上数值有变化，就表明左边对应的物品是被装入的，然后用当前容量减去该物品的容量，得到在该容量下的最大价值。重复这个过程，向上，如果数值没有变化，如图中虚线框的8到实现框的8部分，说明得到最大价值时，左边的几个物品没有放入。当发生值改变时，如图中实线框8的上面是3，则重复前面的过程，用此时背包的容量减去左边物品的质量，7 kg-4 kg=3 kg，在背包的容量为3 kg时，最大价值就是装入第1个物品得到的3。所以装入方案为：选择质量为3 kg、价值为3的物品，质量为4 kg、价值为5的物品和质量为5、价值为8的物品，得到最大总价值为8+5+3=16，所占总容量为3 kg+4 kg+5 kg=12 kg。

例3.11　最短路径求解问题：找出图3.27所示的矩阵中从左上角到右下角的最小路径和，假设只能向下和向右移动。

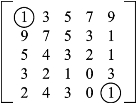
图3.27　最短路径求解问题

解　（1）分析最后一步的计算，看看能否转化为子问题。和上一个例子类似，假设最后一点坐标为（i，j），从左上角到达时的最小距离为DP［i，j］。由例题条件知，DP［i，j］的值一定是其上一点DP［i，j-1］或左边点DP［i-1，j］再加上（i，j）这点的坐标值L［i，j］得到的，所以也就将求DP［i，j］变成了求DP［i，j-1］或DP［i-1，j］，然后选其中值较小的加上L［i，j］，于是得到式（3.4）：

（2）存储：用二维矩阵对应位置存储起点到当前点的最小路径和。

（3）初始条件和边界等限制情况：第1行和第1列就只有1条路径，可以直接计算。

（4）计算顺序，第1行开始，从左往右，从上到下。

计算过程在此省略，可以作为练习推导或者编程实现试一下，最后可计算出本题答案为19。