博弈树：理解博弈竞争过程的非合作指南

博弈是参与的各方互为对手竞争的过程。其中零和博弈（zero-sum game）是一种简单且典型的博弈过程。它是指参与博弈的各方收益和损失相加总和永远为零，以一方战胜其他方为目的，参与的各方可以轮流采取行动或者同时采取行动，属于非合作博弈。比如下棋就属于零和博弈。为了进一步简化，还假定博弈过程具有非偶然性和全信息性。非偶然性是指参与方都根据自己的利益得失来理智地选择每一步策略，不存在偶然失误等随机因素；全信息性指的是博弈的规则、当前的格局以及过去的历史为大家所共知，任何一方都能认识到每一步策略对大家可能造成的影响。

这里介绍的博弈树搜索（game tree search）就是用于零和博弈过程，并假定满足非偶然性和全信息性。以两人博弈为例，假定博弈中的双方为A和B（也常被称为MAX和MIN），双方具有相同的关于状态空间的知识，轮流采取行动，结果只有3种情况：A胜、B胜和平局。在博弈过程中，双方都需要了解当前的格局及过去的历史，选取对自己最有利和对对手最不利的策略。

假如A代表我方，B是对手，那么可供我方选择的若干行动方案之间就是或关系，因为我方可以选其中任意一种作为行动方案。我方自然会选择对自己最优的路径。在我方行动方案的基础上，对手也有若干可选择的行动方案，这些行动方案对我方来说，就相当于是与关系，因为我方要考虑对手的所有方案，换句话来说，就是要考虑到最坏的情况，即对手会选择对我方最不利的行动方案。这样扩展开来，得到的与或树就称为博弈树。

于是，博弈的初始格局即为初始状态节点，我方扩展的节点是或节点，对手扩展的节点为与节点。由于我方和对手轮流采取行动，双方轮流扩展节点，因此或节点和与节点逐层交替出现。所有使我方获胜的终局都是本原问题，相应节点就是可解节点。所有使对手获胜的终局节点都是不可解节点。接下来，问题就变成了如何选一个对我方最有利的行动方案。这就是博弈搜索中常用的极小极大搜索（minimax search）。它是香农在1950年提出来的。其中，MAX方尽量使得自己的优势最大、得分最高，所以MAX方会选择极大值；MIN方则会尽量使MAX方的得分最低，所以MIN方会选择极小值。在与或树搜索中，或节点向上传递的最小值，指的是代价最小，即最优得分最高。下面以一个简单的游戏作为例子进行说明。

例3.6　假设我和你玩一种游戏：有一堆牌，我和你必须轮流对它进行分堆操作，分成数量不等的两堆，谁最先没办法继续分堆了，那么谁就输了。比如，4张牌可以分成3张和1张，但是不能分为2张和2张。为了简化，假设这堆牌总共有7张，请用极小极大搜索证明后走的总有可能会胜利。

解　首先，按照游戏规则获得游戏过程的状态图，设定MIN方先走，按游戏顺序分层，并为每个端节点加上标志1或者0，1代表MAX方胜利，0代表MAX方失败，也就是MIN方胜利，如图3.19所示。状态节点中的数字代表着牌被分成的状态，比如［2，2，2，1］代表着牌被分成了4堆，有3堆是2张还有1堆是1张，此时归MAX方行动，而且，MAX方已经无法再将其中某堆牌分成数量不等的2堆了，也就是到了这一步，MAX方会失败，所以标记为0。

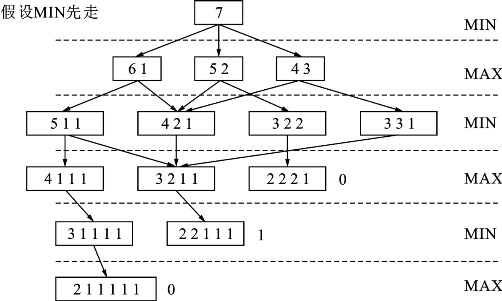
图3.19　例3.6的状态空间图

接下来，进行极小极大搜索（类似于在与或树中由端节点开始向上进行标注），如果父节点是MAX节点，则将孩子节点中的最大值传给它；如果父节点是MIN节点，则将孩子节点中的最小值传给它，于是得到标注后的状态空间图，如图3.20所示。

从图3.20中可以看到，后走的MAX方始终能找到一条使其端节点的标志为1的路径，即后走的一方总有机会赢。

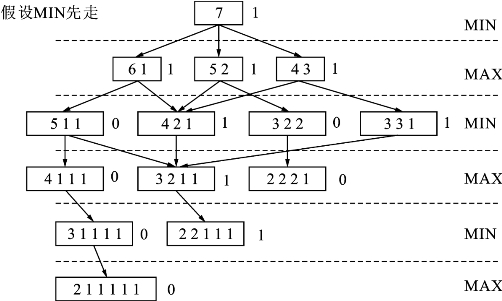
图3.20　例3.6经过极小极大搜索标注后的状态空间图

本章“思考与练习”中的第7题是余一棋游戏（the nim number game），和例3.6类似，可以试着玩一下这个游戏。(www.xing528.com)

从极小极大搜索的过程可以推出博弈树搜索的时间复杂度与空间复杂度和深度优先搜索类似。在很多情况下，博弈的状态空间无法一直展开到端节点，无法进行穷举搜索，所以通常会采用固定层深的极小极大搜索。这称为n层预判（n-ply look ahead）。此时，最后一层的节点相当于端节点，但是由于并不是博弈的最终状态，因此无法以胜负来直接赋值，但是可以使用启发函数进行赋值，并向上传播到达当前状态，从而获得从当前状态出发，经过n次移动后可以达到具有最佳启发值的路径。

和前面一样，如果父状态在MIN层，则传最小值，如果父状态在MAX层，则传最大值，也就是努力使MIN层的父状态最小化，使MAX层的父状态最大化。

小时候，大家可能玩过一种井字棋的游戏（Tic-Tac-Toe）：在一个3×3的九宫格棋盘内，两个人轮流画上自己的棋子×或者○，谁先把自己的棋子连成3个在同一行、同一列或者同一斜线上，谁就赢了。

为这个游戏可以设计一种启发信息，比如计算MAX方存在的所有胜利路径数和MIN方存在的所有胜利路径数之差。图3.21所示的是井字棋游戏中的一种状态，×可能胜利路径数为6，○可能胜利路径数为5，因此启发值c（n）=6-5=1。

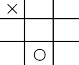
图3.21　井字棋游戏的一种状态

通过2层预判的极小极大搜索就可以得到如图3.22所示的搜索过程。

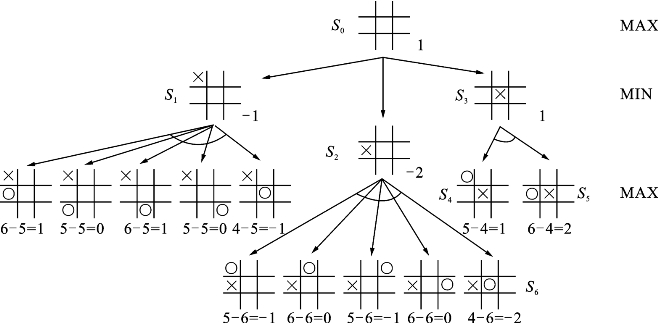
图3.22　井字棋游戏2层预判极小极大搜索过程

这里，×是MAX方，○为MIN方，双方进行博弈。在图中所示2层预判的基础上可以知道，×方应该选启发值最大的，即由S0到S3是最佳路径；此时○方的最优选择是希望使启发值最小，所以○方这时的最佳路径为S4。假如×方并不太聪明，选择了S2，那么对于○方来说，S6将是最佳选择。

井字棋游戏的实现在本章实验参考部分的第三个实验里，提供的Python参考代码使用了极小极大搜索来实现这个游戏，在实验中请试着修改代码利用启发信息来实现固定2层或3层深度的极小极大搜索，并进行对比。

利用启发信息采用固定层深的极小极大搜索可以减少每次做决策的搜索量，然而有可能会产生地平线效应（horizon effect），也就是最远只能看到固定层深，也就是地平线处，看不到地平线以外的状态，所以可能会被有限层深度的特别好状态引诱而导致错误的选择。如果深度设得过大，还有可能导致评估的结果存在偏差。另一种缩小搜索空间的方法称为剪枝技术，接下来介绍α-β剪枝技术。