与或树（and or tree）是一种对复杂问题的简化方法。当一个问题，称之为父问题，可以分解为若干子问题时，这个父问题就变成了具有与关系的若干子问题，子问题之间用一段小圆弧连接标记。当把一个问题进行等价变换，变换成其他容易求解的新问题时，新问题和父问题之间就构成了或关系。于是，有了与树、或树、与或树的概念，如图3.15（a）、（b）、（c）表示。其中，与或树表示父问题既经过了分解，又经过了等价变换。
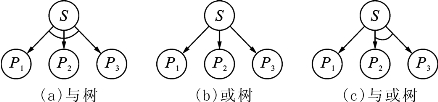
图3.15 与树、或树、与或树
先来看一些概念解释。
本原问题：不能再分解或变换的，且直接可解的子问题。
端节点：与或树中没有子节点的节点。本原问题所对应的节点显然属于端节点，它又称为终止状态节点，一般用t标记。
可解节点：有三种类型，终止状态节点、至少有一个子节点可解的或节点、全部子节点都可解的与节点，都称为可解节点，其他为不可解节点。
解树：由可解节点构成，且由可解节点能推出初始状态节点的子树。一棵与或树可以有存在解树、不存在解树或有多个解树等情况。
与或树搜索和前面介绍过的其他搜索过程也是相似的，基本流程如图3.16所示，主要不同之处在于；对当前节点进行扩展时，与或树搜索使用的是分解（与节点）或等价变换（或节点）操作。所以它比较适合用于推理。同时，与或树搜索还需要根据子节点来回溯标记父节点、祖先节点的可解性，这一过程也称为可解标记过程或不可解标记过程。因此，与或树搜索扩展子节点时还需要为其设置指向父节点的指针。对于与节点，要确定其父节点可解，必须确定该父节点的所有子节点都可解。对于或节点，一旦找到了某个节点可解就可以确定其父节点可解了；而如果搜索到某个或节点不可解，则可以回溯去搜索另一个分支。从这个意义上来说，如果是只有或节点的或树，搜索就和深度优先搜索一样了。
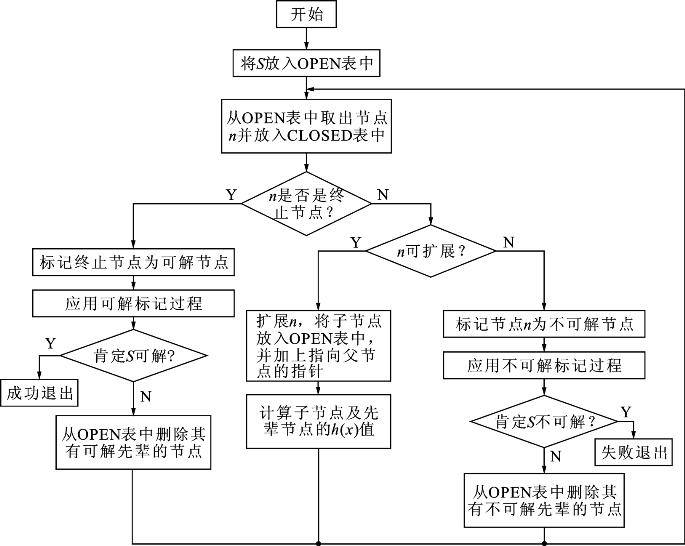
图3.16 与或树搜索流程图
有了可解标记过程、不可解标记过程，可以很好地提高搜索效率。如果判定某个节点为可解节点，则其不可解的后裔可以删去。如果某个节点为不可解节点，则其全部后裔节点都可删去，但当前这个不可解节点还不能删去，因为在判断其先辈节点的可解性时还会用到。通常，会一直向上标记到初始问题是否可解，这样，在博弈中，把胜利或者失败的状态节点作为终止状态节点，当搜索到终止状态节点时，就可以通过可解标记过程来知道初始状态节点沿着某条路径最终是会失败还是获胜了。
先来看一个将与或图用于命题推理的例子。
例3.4 假设以下命题逻辑为真：
a
b
c
a∧b→d
a∧c→e(www.xing528.com)
b∨c→f
a∧f→s
请判断：s是否为真？如果b不再为真，s是否依然为真？
解 按照已知逻辑可以画出如图3.17所示的与或图，将s设置为初始状态节点进行与或图搜索，应用可解标记过程，就可以发现s为真，如果b不为真，s依然为真。图3.17（a）所示为b是真的情况，图3.17（b）对应的是b为假的情况，其中t标记为终止节点，灰色代表着可解节点的标记。编程实现时，可解标记通常用一个变量使其为true或false来记录。
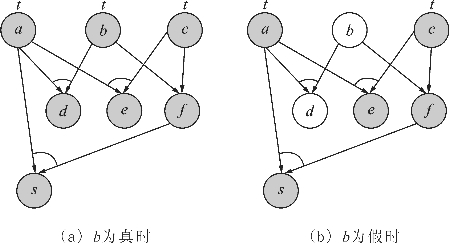
图3.17 例3.4与或图
在博弈过程中，往往存在多个可解路径，除了需要找到可解路径以外，还需要找最优路径，这就要考虑路径所消耗的代价了。给与或树的每一条搜索路径以及节点标上所需耗费的代价值，就得到了代价与或树，这样就可以通过计算代价来评估选择某一节点路径的好坏了。关于与或树的代价计算有以下一些规定。
（1）如果n是终止状态节点，定义其代价c（n）=0；如果n是端节点，但不是终止状态节点，则定义其代价c（n）=∞。
（2）如果n是或节点，y1，y2，…，yt为其子节点，则n节点代价的计算公式为：c（n）=
（3）如果n是与节点，y1，y2，…，yt为其子节点，则n节点的代价通常用以下两种计算方法中的一种进行计算。
①和代价：
，即取其所有子节点代价的和作为其代价。
②最大代价：
，即取其所有子节点中最大的代价作为其代价。
例3.5 计算图3.18所示的代价与或树的代价。
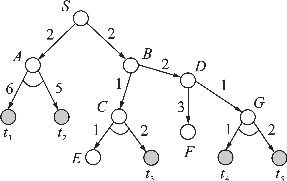
图3.18 例3.5代价与或树
解 由图知，该代价与或树有两个解树，左边解树S、A、t1、t2和右边解树S、B、D、G、t4、t5。
对于左边解树，用和代价计算与节点的代价，得c（A）=11，c（S）=13；用最大代价计算与节点的代价，得c（A）=6，c（S）=8。
对于右边解树，用和代价计算与节点的代价，得c（G）=3，c（D）=4，c（B）=6，c（S）=8；用最大代价计算与节点的代价，得c（G）=2，c（D）=3，c（B）=5，c（S）=7。
可以看出，从S出发，选择右边解树可以得到代价更小的路径。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
