爬山法搜索算法详解

在启发式搜索中，还有一种方法也经常被采用，叫作爬山法搜索，也称为盲人爬山法搜索（blind hill climbing search）。爬山法搜索，顾名思义，就是边探索边逐步往前进，逐步缩短和目标状态节点的距离，也就是先扩展当前状态节点，评估其后继孩子节点，选择最佳的后继孩子节点进行扩展。在这个过程中既不保留兄弟姐妹节点，也不保留父节点，它采用的是一种局部择优的搜索策略，本质上来说，可以看作是一种深度优先的启发式搜索的改进。

可以思考一下，如果我们闭着眼睛爬山，希望尽快达到山顶，不考虑体力问题，那么我们该选哪个方向爬？我们肯定会选朝坡度最大、最陡峭的方向往上爬，即沿斜率最大的方向前进。也就是说采用最陡爬山法，搜索并到达一个节点后，后继状态节点的选择并不是盲目的，而是采用A*搜索方法，使用一个评估函数f（n）来搜索当前最优节点。

盲人爬山法搜索的特点是OPEN表可以取消，每次扩展后继状态节点只保留满足评估函数f（n）的最优孩子节点n＇，其他孩子节点可以全部丢掉。由n＇扩展的节点配上父节点指针后可直接放入CLOSED表中，这样逐步递进。所以说它可以看作是深度优先搜索的一种改进，属于局部择优搜索，因为没有进行全面搜索，所以结果可能不是全局最优解。

在评估函数f（n）=g（n）+h（n）的设计中，g（n）通常按选择节点的深度生成，h（n）则通常选用高度函数H（r）的梯度的绝对值，如下式：

h（n）=|grad（H（r）|　（3.1）

某一点的梯度方向也是该点坡度最陡的方向，然后沿梯度上升方向选择节点进行扩展。在具体设计时，可以建立一个描述节点变化的单极值函数，使极值对应目标状态，选取使函数值增长最大的那条规则作用于节点数据，直到没有规则使函数值继续增长为止。

爬山法搜索在很多情况下是有效的，而且简单，由于取消了OPEN表，处理数据量大大减少，因而速度非常快。但是它也有非常明显的局限性，由于它属于局部最优算法，只适合用于单因素、单极值的情况，在处理多峰值、盆地、山脊、断层问题时，会出现搜索失败。(www.xing528.com)

下面分别看一下这几种情况。

多峰值：当遇到一阶导数（或偏导数）为0的节点有好几个时，如果找到某个极大值，即便不是全局最大值，也不会再移动了，因为往其他任何方向继续搜索，都是下降，于是会陷入局部最优解。如图3.14所示，当从S1搜索到B时，B点无论朝前或朝后走，都将使得高度下降，所以将不再前进。为了解决这个问题，可以采取换其他的路径走的方法。比如可以随机多选一些起点，分别获得最优解，选择所有最优解中的最优者作为全局最优解。再比如，可以引入回溯机制，退回去重新选择其他路径。引入回溯机制就需要记录之前走过的路径。

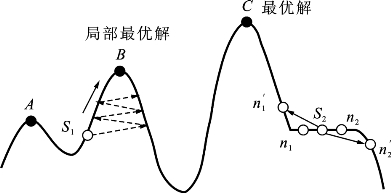
图3.14　爬山法搜索中的常见问题

高原：周围都是平地，导数处处为0。这将导致无法知道该选哪个方向最佳。如图3.14中S2所处位置，如果扩展出n1，n2两个节点，则高度H（n1）与H（n2）相同，计算出的梯度值都是0，无法确定下一步选n1还是n2，才会使H（n）高度值上升。可以采取的解决办法是扩展节点时进行大的跳跃，比如扩展出两个步伐远一点的点n＇1和n＇2。

山脊：搜索可能会在山脊的两面来回振荡，导致搜索效率较低，如图3.14虚线路径所示。

断层：搜索区域出现断层，使得一阶导数不连续，使人误以为已经到达目的地。