贪心法搜索优化方案

贪心法搜索（greedy search），也称为最佳者优先搜索（best first search），是在宽度优先搜索的基础上，对于下一步可以扩展出的状态节点，找可能是距离目标状态节点最近的节点进行扩展。启发信息就是去估计这些节点和目标状态节点之间的距离。所以，贪心法搜索的流程依然和图3.1类似，只是在扩展节点时需要借助启发信息，使用和代价树的宽度优先搜索类似的优先级队列来实现。

比如还是针对找出从武汉到北京经过各省会城市的最短路径这个问题，可以在搜索路径之前，先根据经纬度或地图坐标，计算出每个省会城市到北京的直线距离，将其作为启发信息，接下来，扩展节点时，就可以参考启发信息，寻找孩子节点中距离目标状态节点最近的节点进行扩展。从武汉可以到达的相邻省会城市有西安、重庆、长沙、南昌、合肥、郑州6个，它们距离北京的直线距离千米数分别约为906，1457，1340，1251，898，622，按照贪心的原则，首先选择郑州节点进行扩展。接着从郑州扩展节点也是如此，直到最后到达北京。

同样，在进行节点扩展时，需要判断扩展出的孩子节点是否已经在OPEN表或者CLOSED表中，如果不在就根据启发信息算出该节点距离目标状态节点的启发值，然后添加进OPEN表中并排序。如果在OPEN表中，就检查启发值是否比OPEN表中的更优，是就替换掉并重新排序。如果在CLOSED表中，并且启发值比CLOSED表中的更优，就移除CLOSED表中的节点，将新节点添加进OPEN表中并排序。

贪心法搜索的实现代码和代价树的宽度优先搜索基本相同，只是将代价树的宽度优先搜索中的计算代价部分换成了计算启发值。贪心法搜索的优点是通常能较快地找到目标状态节点，效率很高。在图3.9中，左图为代价树的宽度优先搜索过程示意，右图为贪心法搜索过程示意，深色方格代表已经探索过的节点，有深色边框的方格代表还在OPEN表中的节点，白色粗线即为找到的路径。贪心法搜索总是选择可能离目标状态节点最近的节点进行扩展，所以只搜索了很少一部分状态就找到了目标状态节点；而代价树的宽度优先搜索朝每个方向都扩展，从中选择代价最小的节点，搜索的状态多了许多。

图3.9　代价树的宽度优先搜索和贪心法搜索对比

贪心法搜索的缺点也很明显，它在对问题求解时，总是做出在当前看来是最好的选择，并不是从整体最优上进行考虑，因此并不能保证找到的解是最优解。如果对图3.8用贪心法搜索来实现，假设选用距离终点GOAL的直线距离作为启发值，那么找到的路径将会是START-e-r-f-GOAL，距离为15，并不是最佳路径。从图中看e离目标状态节点最近，但实际中从起点直接到e中间可能有障碍物，导致需要绕路或者路径弯曲，进而导致实际代价其实很高。图3.10也说明了这种情况，左图采用代价树的宽度优先搜索，前面已经介绍过代价树的宽度优先搜索具有最优性，也就是能找到最短路径；右图采用贪心法搜索，采用曼哈顿距离作为启发函数，在Python中，可以这样定义该函数：(www.xing528.com)

采用贪心法搜索，障碍物的存在导致搜索到的路径并不是最优路径。

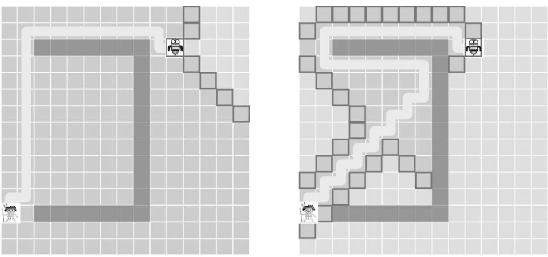
图3.10　有障碍物时代价树的宽度优先搜索和贪心法搜索对比

可见，代价树的宽度优先搜索虽然效率不高，但具有最优性，可以保证得到最优解，因为它所依据的是从初始状态节点到当前状态节点的实际代价，始终选取代价最小的节点。而在贪心法搜索中，使用的是启发信息，它是对当前状态节点到目标状态节点的估计信息，如果启发信息不合理或者不全面就可能导致路径不一定是最优路径。

如果能结合这两种搜索的优点，就能既提高搜索效率又找到最优解。那么，有办法结合这两种搜索的优点吗？下面介绍的A*搜索（a star search）就是结合了这两种搜索的优点的一种算法。